Статистичні формули

за Редакція 1 Серпня, 2023 Статистика 0 коментарів

Тут ви знайдете основні статистичні формули. Ми також залишаємо вам посилання на наші статті, у яких ви можете побачити приклади застосування кожної статистичної формули, а також, крім того, ви можете скористатися онлайн-калькулятором, щоб не робити розрахунки та знати результат формули безпосередньо.

Формули для статистичних мір центральної тенденції

половина

Щоб обчислити середнє значення, додайте всі значення, а потім розділіть на загальну кількість даних. Таким чином, формула середнього значення виглядає наступним чином:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

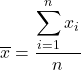
У статистиці середнє також відоме як середнє арифметичне або середнє .

➤ Див.: Калькулятор середнього арифметичного

Медіана

Медіана – це середнє значення всіх даних, упорядкованих від найменшого до найбільшого. Іншими словами, медіана ділить упорядкований набір даних на дві рівні частини.

Розрахунок медіани залежить від того, парна чи непарна загальна кількість даних:

Якщо загальна кількість даних непарна , медіаною буде значення, яке потрапляє прямо в середину даних. Тобто значення, яке знаходиться в позиції (n+1)/2 відсортованих даних.

$Me=x_{\frac{n+1}{2}$

Якщо загальна кількість точок даних парна , медіана буде середнім значенням двох точок даних, розташованих у центрі. Тобто середнє арифметичне значень, які знаходяться в позиціях n/2 і n/2+1 упорядкованих даних.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

золото

$n$

це загальна кількість даних у вибірці, а символ Me вказує на медіану.

➤ Див.: калькулятор медіан

Мода

У статистиці мода – це значення в наборі даних, яке має найвищу абсолютну частоту, тобто мода – це найбільш повторюване значення в наборі даних.

Тому немає конкретної формули для режиму, але щоб обчислити режим набору статистичних даних, просто підрахуйте, скільки разів кожен елемент даних з’являється у вибірці, і дані, які найбільше повторюються, будуть режимом.

Режим також можна назвати статистичним режимом або модальним значенням .

➤ Дивіться: Модний калькулятор

Формули для статистичних мір дисперсії

Стандартне відхилення

Стандартне відхилення, яке також називають стандартним відхиленням, дорівнює кореню квадратному із суми квадратів відхилень ряду даних, поділеного на загальну кількість спостережень.

Таким чином, формула стандартного відхилення :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Див.: Калькулятор стандартного відхилення

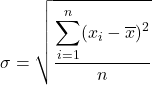
Дисперсія

Дисперсія дорівнює сумі квадратів залишків над загальною кількістю спостережень. Отже, формула для цієї статистичної метрики така:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

золото:

$X$

це випадкова змінна, для якої потрібно обчислити дисперсію.
$x_i$

це значення даних

$i$

.
$n$

– загальна кількість спостережень.
$\overline{X}$

є середнім значенням випадкової величини

$X$

.

➤ Дивіться: Калькулятор розриву

Коефіцієнт варіації

У статистиці коефіцієнт варіації — це міра дисперсії, яка використовується для визначення дисперсії набору даних відносно його середнього значення. Коефіцієнт варіації обчислюється шляхом ділення стандартного відхилення даних на його середнє значення, а потім множення на 100, щоб виразити значення у відсотках.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Дивіться: Калькулятор коефіцієнта варіації

охайний

Статистичний діапазон — це міра дисперсії, яка вказує на різницю між максимальним і мінімальним значенням даних у вибірці. Таким чином, щоб обчислити обсяг генеральної сукупності або статистичної вибірки, максимальне значення необхідно відняти від мінімального значення.

$R=\text{M\'ax}-\text{M\'in}$

➤ Див.: Приклад статистичного діапазону

Міжквартильний діапазон

Міжквартильний діапазон , також званий інтерквартильним діапазоном , є мірою статистичної дисперсії, яка вказує на різницю між третім і першим квартилями.

Тому, щоб обчислити інтерквартильний діапазон набору статистичних даних, ви повинні спочатку знайти третій і перший квартилі, а потім відняти їх.

$IQR=Q_3-Q_1$

➤ Див.: Калькулятор інтерквартильного діапазону

середня різниця

Середнє відхилення , яке також називають середнім абсолютним відхиленням , є середнім значенням абсолютних відхилень. Отже, середнє відхилення дорівнює сумі відхилень кожного елемента даних від середнього арифметичного, поділеному на загальну кількість елементів даних.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Див.: калькулятор середнього відхилення

Формули для статистичних вимірювань положення

квартилі

У статистиці квартилі – це три значення, які ділять набір упорядкованих даних на чотири рівні частини. Таким чином, перший, другий і третій квартилі становлять відповідно 25%, 50% і 75% усіх статистичних даних.

Квартилі представлені великою літерою Q та індексом квартиля, тому перший квартиль – Q ₁ , другий квартиль – Q ₂ , а третій квартиль – Q ₃ .

Формула квартиля :

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Будь ласка, зверніть увагу: ця формула повідомляє нам позицію квартиля, а не значення квартиля. Квартиль буде даними, розташованими в позиції, отриманій формулою.

Однак іноді результат цієї формули дає нам десяткове число. Тому ми повинні розрізняти два випадки залежно від того, чи є результат десятковим числом чи ні:

Якщо результатом формули є число без десяткової частини , квартиль — це дані, які знаходяться в позиції, наданій формулою вище.
Якщо результатом формули є число з десятковою частиною , значення квартиля обчислюється за такою формулою:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Де x _i і x _i+1 — номери позицій, між якими знаходиться число, отримане за першою формулою, а d — десяткова частина числа, отриманого за першою формулою.

➤ Див.: Квартильний калькулятор

децилі

У статистиці децилі – це дев’ять значень, які ділять набір упорядкованих даних на десять рівних частин. Таким чином, перший, другий, третій,… дециль представляє 10%, 20%, 30%,… вибірки чи сукупності.

Децилі позначаються великою літерою D і децильним індексом, тобто перший дециль — D ₁ , другий — D ₂ , третій — D ₃ і т. д.

Децильна формула виглядає наступним чином:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Будь ласка, зверніть увагу: ця формула повідомляє нам позицію дециля, а не значення дециля. Дециль буде даними, розташованими в позиції, отриманій формулою.

Однак іноді результат цієї формули дає нам десяткове число, тому ми повинні розрізняти два випадки залежно від того, чи є результат десятковим числом чи ні:

Якщо результатом формули є число без десяткової частини , дециль — це дані, розташовані в позиції, передбаченій формулою вище.
Якщо результатом формули є число з десятковою частиною , децильне значення обчислюється за такою формулою:

$D=x_i+d\cdot (x_{i+1}-x_i)$

➤ Див. Децильний калькулятор

процентилі

У статистиці процентилі – це значення, які ділять набір упорядкованих даних на сто рівних частин. Таким чином, процентиль вказує значення, нижче якого опускається відсоток набору даних.

Процентиль позначається великою літерою P та індексом процентиля, тобто перший процентиль — P ₁ , 40-й процентиль — P ₄₀ , 79-й процентиль — P ₇₉ тощо.

Формула процентиля :

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Будь ласка, зверніть увагу: ця формула повідомляє нам положення процентиля, але не його значення. Процентиль – це дані, розташовані в позиції, отриманій формулою.

Якщо результатом формули є число без десяткової частини , процентиль відповідає даним, які знаходяться в позиції, наданій формулою вище.
Якщо результатом формули є число з десятковою частиною , точне значення процентиля обчислюється за такою формулою:

$P=x_i+d\cdot (x_{i+1}-x_i)$

➤ Див.: Калькулятор процентилів

Статистичні формули вимірювання форми

коефіцієнт асиметрії

Коефіцієнт асиметрії, або індекс асиметрії, — це статистичний коефіцієнт, який використовується для визначення асиметрії розподілу. Отже, розрахувавши коефіцієнт асиметрії, ви можете дізнатися тип асиметрії розподілу без необхідності робити його графічне представлення.

Формула для коефіцієнта асиметрії має такий вигляд:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Для розрахунку коефіцієнта асиметрії Фішера можна використовувати будь-яку з наступних двох формул:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

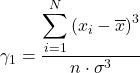
золото

$E$

є математичне сподівання,

$\overline{x}$

середнє арифметичне,

$\sigma$

стандартне відхилення і

$n$

загальна кількість даних.

➤ Див.: Коефіцієнт асиметрії

коефіцієнт ексцесу

Ексцес, також званий різкістю, вказує на те, наскільки концентрований розподіл навколо свого середнього значення. Іншими словами, ексцес показує, чи є розподіл крутим чи плоским. Зокрема, чим більший ексцес розподілу, тим він крутіший (або різкіший).

Формула для коефіцієнта ексцесу має такий вигляд:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

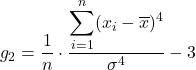
золото

$x_i$

це значення, що відповідає спостереженню

$i$

$\overline{x}$

середнє арифметичне,

$\sigma$

стандартне відхилення і

$n$

загальна кількість даних.

➤ Див.: Калькулятор коефіцієнта зведення

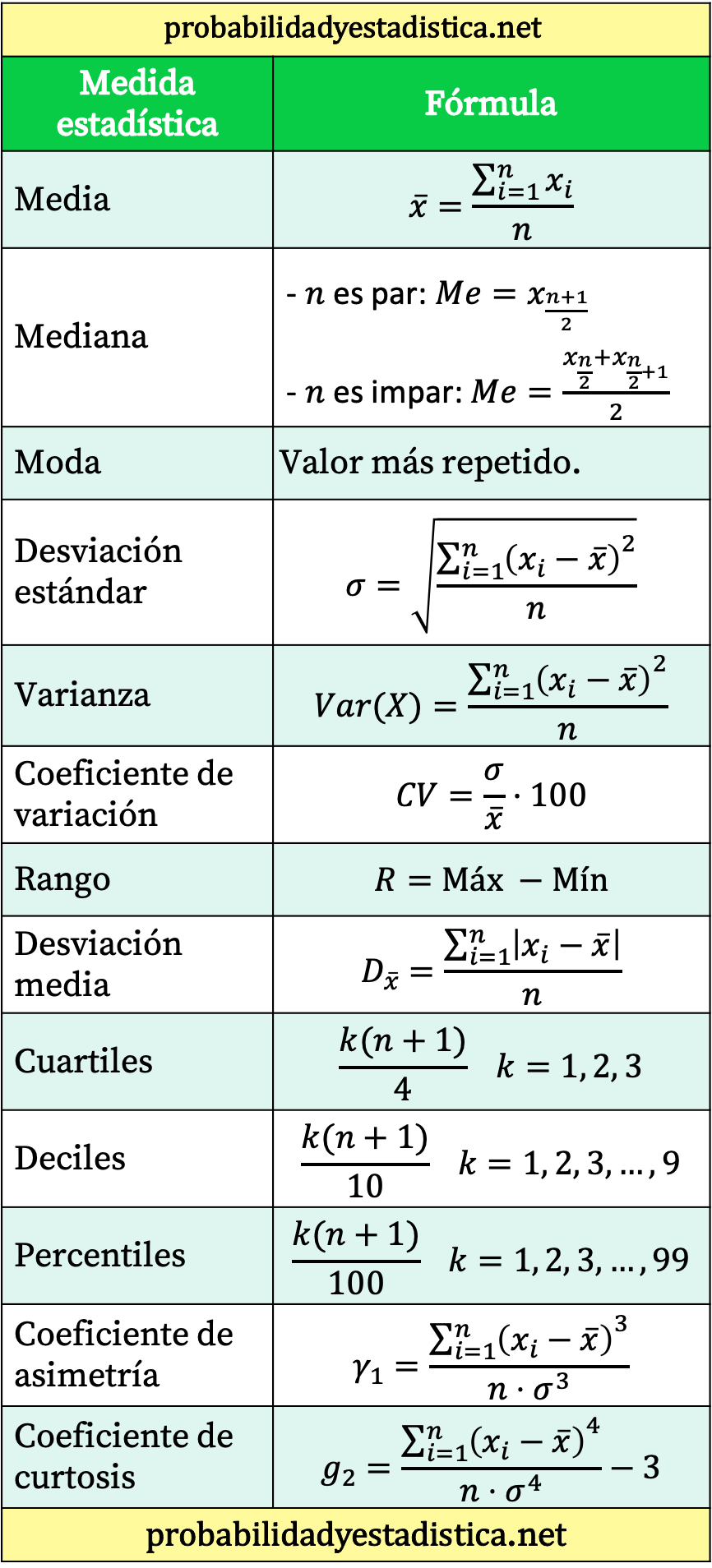
Зведена таблиця всіх статистичних формул

Нарешті, ми залишаємо вам таблицю, яка підсумовує основні статистичні формули.

➤ Див.: Формули ймовірності

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Формули для статистичних мір центральної тенденції

половина

Медіана

Мода

Формули для статистичних мір дисперсії

Стандартне відхилення

Дисперсія

Коефіцієнт варіації

охайний

Міжквартильний діапазон

середня різниця

Формули для статистичних вимірювань положення

квартилі

децилі

процентилі

Статистичні формули вимірювання форми

коефіцієнт асиметрії

коефіцієнт ексцесу

Зведена таблиця всіх статистичних формул

Про автора

Редакція

Додати коментар