Схема стебла і листя

У цій статті пояснюється, що таке діаграми стебла та листя в статистиці та для чого вони використовуються. Таким чином, ви дізнаєтесь, як побудувати діаграму «стебло-лист», розв’яжете вправи для цього типу статистичних графіків і, нарешті, які переваги та недоліки діаграми «стебло-лист».

Що таке діаграма стебло-лист?

Діаграма стебла та листя — це тип статистичної діаграми, на якій представлено набір кількісних даних.

На діаграмі «стебло-лист» кожна точка даних відокремлена листом , який є його останньою цифрою, і стеблом , які є рештою цифр. Отже, на діаграмі «стебло-лист» кожен листок розміщений на лінії відповідного стебла.

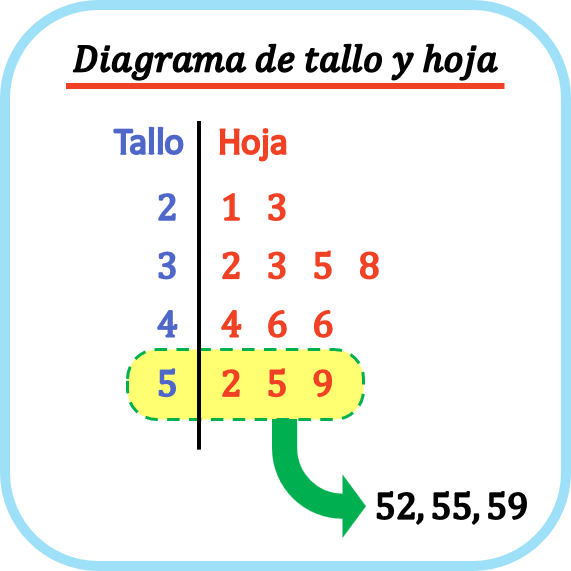
Таким чином, графіки стебла та листя допомагають графічно представити набір статистичних даних, а також допомагають візуалізувати форму розподілу.

Діаграма стебла та листя також відома як діаграма стебла та листя , назва походить від англійської мови.

Побудова стебла та листя дуже схожа на гістограму , хоча цей інший тип статистичного графіка використовується для більших розмірів вибірки.

Як створити схему стебла та листя

Щоб створити діаграму стебла та листя, виконайте такі дії:

1. Відсортуйте дані від найменшого до найбільшого.
2. Якщо необхідно, округліть числа до потрібної кількості цифр.
3. Визначте, в якій фігурі буде зроблений розріз між стеблом і листком, тобто визначте кількість фігурок, які будуть мати листя. Як правило, аркуш розроблено таким чином, щоб містити лише останню цифру кожного елемента даних.
4. Представте кожну частину даних на діаграмі стебла та листя. Стебла розміщуються в лівій колонці в порядку зростання, тоді як листя розміщуються в правій колонці на висоті відповідного стебла, а також у порядку зростання.

Приклад графіка стебла та листя

Щоб ви могли побачити, як створити діаграму стебла та листя, ми розв’язуємо два приклади нижче: один без десяткових знаків, а інший із десятковими знаками.

Приклад 1

• Побудуйте наступний ряд даних на діаграмі стебла та листя:

У цьому випадку дані вже впорядковані та округлені, тому немає необхідності виконувати ці два кроки. Отже, оскільки числа мають дві цифри, вони будуть представлені так, що часи є основою, а одиниці – листами графіка.

Спочатку ми представимо основу діаграми. Час даних досягає 9, тому ми робимо рядок для кожного десятка:

Потім ми представляємо листя, для цього ми розміщуємо одиницю кожного з даних у відповідному рядку. Наприклад, число 57 піде до кореня 5, а в правій колонці ми додамо 7.

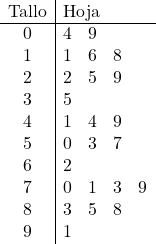
Таким чином, усі вибіркові дані були представлені на графіку стебла та листя.

Приклад 2

• Порівняйте наступні два зразки даних з десятковими дробами, використовуючи графік стебла та листя.

Як ви побачите в цій вправі, один графік стебла та листя можна використовувати для представлення двох статистичних вибірок. Тому ми нанесемо обидва набори даних на одну діаграму стебла та листя: один ліворуч і один праворуч. Такий тип ділянки називається двостовбурно-листяною .

У цьому випадку ми візьмемо цілу частину чисел як основу діаграми, а з іншого боку, десяткові дроби будуть листами діаграми. Тому ми створюємо макет стебла та листя, розміщуючи всі цілі частини:

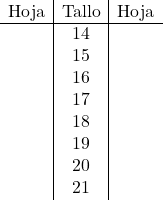
А тепер ми розміщуємо аркуш із кожними даними у відповідній йому стеблі:

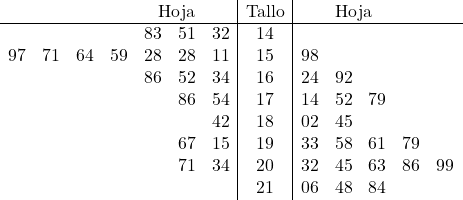
Представляючи дані графічно, ми можемо легко порівнювати їх. Зокрема, ми бачимо, що вибірка даних праворуч трохи більша, ніж вибірка ліворуч, тому її середнє значення також буде більшим. Таким чином, залежно від мети статистичного дослідження, нам буде цікаво вибрати ту чи іншу вибірку.

Майте на увазі, що вам потрібно не лише знати, як побудувати діаграму з похилими лініями та лезами, а й як інтерпретувати діаграму.

Переваги та недоліки стебла та листя

Завдяки особливостям стеблової та листової ділянки, ці типи ділянок мають наступні переваги та недоліки:

Перевага:

• Обведення стебел і листя дозволяє побачити форму розподілу.
• Два розподілу можна порівняти за допомогою графіка подвійного стебла та листя.
• Це дозволяє швидко визначати викиди в наборі даних.
• Визначити режим ряду даних можна на око.

Недоліки:

• Діаграма стебла та листя використовується все рідше, тому що комп’ютерне програмне забезпечення може швидко створити більш складний графік.
• Розмір вибірки для представлення обмежений, зазвичай становить від 15 до 150 точок даних.
• Можуть бути представлені лише кількісні дані.