Що таке y hat у статистиці?

У статистиці термін y hat (пишеться ŷ ) стосується оціненого значення змінної відповіді в моделі лінійної регресії .

Зазвичай ми пишемо оціночне рівняння регресії таким чином:

ŷ = β ₀ + β ₁ x

золото:

• ŷ : оцінене значення змінної відповіді
• β ₀ : Середнє значення змінної відповіді, коли змінна предиктора дорівнює нулю
• β ₁ : середня зміна змінної відповіді, пов’язана зі збільшенням на одну одиницю прогнозної змінної

Наприклад, припустімо, що ми маємо такий набір даних, який показує кількість годин, вивчених шістьма різними студентами, а також їхні підсумкові іспити:

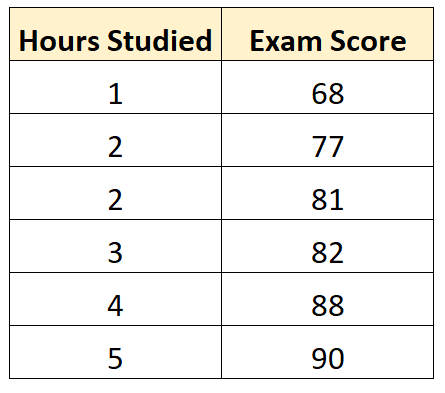
Припустімо, що ми використовуємо статистичне програмне забезпечення (наприклад, R , Excel , Python або навіть вручну), щоб підібрати наступну регресійну модель, використовуючи досліджувані години як змінну прогностику та досліджуючи результати як змінну відповіді:

Оцінка = 66,615 + 5,0769*(години)

Спосіб інтерпретації коефіцієнтів регресії в цій моделі такий:

• Середній бал іспиту для студента, який вивчає нуль годин, становить 66 615 .
• Екзаменаційний бал збільшується в середньому на 5,0769 балів за кожну додаткову вивчену годину.

Ми можемо використовувати це рівняння регресії, щоб оцінити оцінку даного студента на основі кількості вивчених годин.

Наприклад, студент, який навчається 3 години, повинен отримати оцінку:

Оцінка = 66,615 + 5,0769*(3) = 81,85

Чому використовується Y Hat?

Символ «капелюх» в статистиці використовується для позначення будь-якого «розрахункового» терміну. Наприклад, ŷ використовується для позначення оціненої змінної відповіді.

Як правило, підбираючи моделі лінійної регресії, ми використовуємо вибірку даних із сукупності, оскільки це зручніше та займає менше часу, ніж збір даних для кожного можливого спостереження в сукупності.

Отже, коли ми знаходимо рівняння регресії, ми лише оцінюємо справжній зв’язок між змінною предиктором і змінною відповіді.

Ось чому ми використовуємо член ŷ у рівнянні регресії замість y.

Додаткові ресурси

Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Ознайомлення зі змінними пояснення та відповіді