Теорема байєса

за Редакція 1 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке теорема Байєса та для чого вона використовується в ймовірності та статистиці. Таким чином, ви дізнаєтесь, що таке формула теореми Байєса, розв’яжете приклади теореми Байєса та які застосування цієї теореми.

Що таке теорема Байєса?

У теорії ймовірностей теорема Байєса — це закон, який використовується для обчислення ймовірності події, коли відома апріорна інформація про цю подію.

Точніше, теорема Байєса математично пов’язує ймовірність події A при даній події B з ймовірністю B при даній A.

Наприклад, якщо вам заздалегідь відома ймовірність того, що у людини буде головний біль, коли вона захворіє на грип, ви можете використовувати теорему Байєса, щоб визначити ймовірність того, що людина захворіє на грип, коли у неї буде головний біль.

Теорема Байєса має багато застосувань, наприклад, вона використовується в медицині, економіці чи техніці для розрахунку ймовірностей певних подій, зумовлених іншими подіями. Нижче ми детально розглянемо різні застосування теореми Байєса.

Теорема Байєса була винайдена англійським математиком Томасом Баєсом (1702-1761), хоча вона була опублікована посмертно в 1763 році.

➤ Див.: Умовна ймовірність

Формула теореми Байєса

Теорема Байєса говорить, що заданий простір вибірки, що складається з набору взаємовиключних подій {A ₁ , A ₂ ,…, A _i ,…, A _n }, імовірності яких не дорівнюють нулю, та іншої події B , ми можемо математично пов’язати умовне ймовірність A _i за умови події B з умовною ймовірністю B за даної A _i .

Отже, формула для теореми Байєса , також відомої як правило Байєса , має такий вигляд:

золото:

$P(A_i|B)$

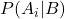
це умовна ймовірність події A _i заданої події B, яка називається апостеріорною ймовірністю.
$P(B|A_i)$

є умовною ймовірністю події B за даної події A _i .
$P(A_i)$

це ймовірність того, що подія A _i відбудеться, яка називається апріорною ймовірністю.

Зверніть увагу, що знаменником формули теореми Байєса є повна ймовірність події B.

Приклад теореми Байєса

Коли ми побачимо визначення теореми Байєса та її формулу, ми побачимо розв’язаний приклад того, як обчислюється ймовірність за допомогою теореми Байєса, щоб краще зрозуміти концепцію.

Магазин електроніки продає телевізори трьох марок: X, Y, Z. За підрахунками, 20% продажів припадає на телевізори марки з дефектами, 3% телевізорів марки Y є дефектними, а телевізори марки Z – на 4%. З огляду на несправний телевізор, яка ймовірність того, що це телевізор марки Z?

Вправа дає нам ймовірність того, що клієнт придбає кожну марку телевізора:

Подія A ₁ : Клієнт купує телевізор марки X → P(A ₁ )=0,20
Подія A ₂ : Клієнт купує телевізор марки Y → P(A ₂ )=0,50
Подія A ₃ : Клієнт купує телевізор марки Z → P(A ₃ )=0,30

Крім того, зчитування також дає нам ймовірність того, що телевізор кожного бренду несправний:

Подія Б: Телевізор несправний

B|A ₁ : Враховуючи телевізор марки X, телевізор несправний → P(B|A ₁ )=0,05
B|A ₂ : Враховуючи телевізор марки Y, телевізор несправний → P(B|A ₂ )=0,03
B|A ₃ : якщо телевізор марки Z, телевізор несправний → P(B|A ₃ )=0,04

Отже, дерево ймовірностей усіх подій, які нас цікавлять, виглядає наступним чином:

Отже, щоб обчислити ймовірність того, що, враховуючи несправний телевізор, це марка Z, ми повинні використовувати формулу з теореми Байєса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

Використовуючи термінологію, використану в цьому прикладі, формула Байєса виглядає так:

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Таким чином, розрахунок ймовірності того, що даний несправний телевізор є маркою Z, виглядає наступним чином:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}$

Підсумовуючи, ймовірність того, що якщо телевізор несправний, це марка Z, становить 32%.

Застосування теореми Байєса

Існує багато застосувань теореми Байєса, зокрема:

Медичні тести : Теорема Байєса часто використовується в медицині для визначення ймовірності проходження діагностичних тестів. Наприклад, у випадку тесту на ВІЛ теорему можна використати для розрахунку ймовірності того, що людина дійсно має вірус, якщо результат тесту позитивний.
Фінансовий аналіз : у фінансах теорема Байєса використовується для розрахунку ймовірності того, що певні економічні події, такі як збільшення або зменшення вартості акцій, відбудуться за набору економічних змінних.
Дослідження ринку : теорема Байєса дає змогу визначити, наприклад, ймовірність того, що людина купить товар після перегляду реклами цього товару.
Прогнозування погоди : моделі погоди також використовують теорему Байєса для визначення ймовірності того, що даний прогноз погоди на основі спостережених даних справдиться. Це підвищує точність кліматичних прогнозів.
Комп’ютерна безпека – у сфері кібербезпеки теорему Байєса можна застосувати для визначення ймовірності того, що підозріла діяльність справді є атакою на комп’ютерну систему.

Вирішені задачі теореми Байєса

Вправа 1

Вважається, що 1% населення страждає від певних захворювань. Тест для виявлення цього захворювання точний на 95% для позитивних випадків і на 90% для негативних випадків. Якщо навмання обрана особа має позитивний результат, яка ймовірність того, що вона насправді хвора?

Подивіться рішення

Заява вправи дає нам такі ймовірності:

A ₁ : Людина має захворювання → P(A ₁ )=0,01
A ₂ : Людина не має захворювання → P(A ₂ )=0,99

B: Тест позитивний
B|A ₁ : Тест є позитивним, якщо людина має захворювання → P(B|A ₁ )=0,95
B|A ₂ : Тест є позитивним, якщо людина не має захворювання → P(B|A ₂ )=1-0,90=0,10

Потім, щоб обчислити ймовірність того, що навмання вибрана людина дійсно має захворювання, якщо тест позитивний, необхідно застосувати правило Байєса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}$

Отже, підставляємо значення в формулу і проводимо розрахунок ймовірності:

$\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}$

Коротше кажучи, ймовірність того, що навмання обрана людина має позитивний результат тесту і дійсно має захворювання, становить 8,76%.

Вправа 2

Вважається, що ймовірність того, що акція зросте за один день, становить 40%, що вона залишиться стабільною – 10%, а що вона впаде – 50%. Крім того, ми знаємо, що коли ринок зростає, існує 90% ймовірності того, що фінансовий аналітик спрогнозує це правильно, що коли ринок залишається стабільним, ймовірність того, що прогноз буде правильним, становить 75%, а в разі падіння, ймовірність правильного прогнозу становить 75%. 85%.%. Якщо аналітик передбачає, що ринок впаде, наскільки ймовірно, що він справді впаде?

Подивіться рішення

У цьому випадку оператор вправи надає нам такі ймовірності:

A ₁ : Ринок зростає за один день → P(A ₁ )=0,40
A ₂ : Ринок залишається стабільним протягом одного дня → P(A ₂ )=0,10
A ₃ : Ринок зростає за один день → P(A ₃ )=0,50

Б: Аналітик прогнозує падіння ринку
B|A ₁ : Аналітик правильно прогнозує, що ринок зросте → P(B|A ₁ )=0,90
B|A ₂ : Аналітик правильно передбачає, що ринок залишається стабільним → P(B|A ₂ )=0,75
B|A ₃ : Аналітик правильно прогнозує, що ринок впаде → P(B|A ₃ )=0,85

Щоб визначити вірогідність того, що аналітик спрогнозує, що ринок впаде, і що він правильний, нам потрібно використати формулу теореми Байєса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Підставляємо значення ймовірності в формулу Байєса і обчислюємо ймовірність:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}$

Таким чином, ймовірність того, що аналітик правий, коли каже, що фондовий ринок впаде, становить 49,42%.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке теорема Байєса?

Формула теореми Байєса

Приклад теореми Байєса

Застосування теореми Байєса

Вирішені задачі теореми Байєса

Вправа 1

Вправа 2

Про автора

Редакція

Додати коментар