Тест бартлетта на однорідність дисперсій (визначення та приклад)
Тест Бартлетта — це статистичний тест, який використовується для визначення того, чи є дисперсії між кількома групами рівними.
Багато статистичних тестів (наприклад , односторонній дисперсійний аналіз ) припускають, що дисперсії однакові між вибірками. Для перевірки цієї гіпотези можна використовувати тест Бартлетта.
Наступні кроки пояснюють, як виконати тест Бартлетта.
Примітка. Не плутайте цей тест із тестом сферичності Бартлетта , який використовується для порівняння спостережуваної кореляційної матриці з матрицею ідентичності.
Етапи виконання тесту Бартлетта
Тест Бартлетта використовує такі нульові та альтернативні гіпотези :
H 0 : Дисперсія між кожною групою однакова.
H A : принаймні одна група має дисперсію, яка не дорівнює іншим.
Статистику тесту можна розрахувати наступним чином:
B = (nk)lns 2 – Σ(n j -1)lns j 2 / c
золото:
- n: загальна кількість спостережень у всіх групах
- k: загальна кількість груп
- ln: це означає «натуральний журнал»
- s 2 : об’єднана дисперсія
- n j : кількість спостережень у групі j
- s j 2 : Дисперсія групи j
І де він розраховується наступним чином:
- c = 1 + (1/3(k-1))*(Σ(1/(n j -1)) – (1/(nk))
Ця тестова статистика відповідає розподілу хі-квадрат із k-1 ступенями свободи. Іншими словами, B ~ X 2 (k-1).
Якщо p-значення , яке відповідає тестовій статистиці, нижче певного рівня значущості (наприклад, α = 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що не всі групи мають однакову дисперсію.
Приклад: тест Бартлетта
Припустімо, професор хоче знати, чи призводять три різні методи навчання до різних середніх оцінок на іспитах.
Вона випадковим чином призначає 10 студентам використовувати кожну техніку протягом тижня, а потім дає кожному студенту іспит однакової складності.
Результати іспиту 30 студентів представлені нижче:

Професор хоче виконати односторонній дисперсійний аналіз, щоб побачити, чи призводять три методи до різних середніх балів на іспиті, але вона спочатку повинна виконати тест Бартлетта, щоб переконатися, що три групи мають однакові дисперсії.
Виконувати тест Бартлетта вручну втомливо, тому ми введемо наступні значення даних у калькулятор тесту Бартлетта :
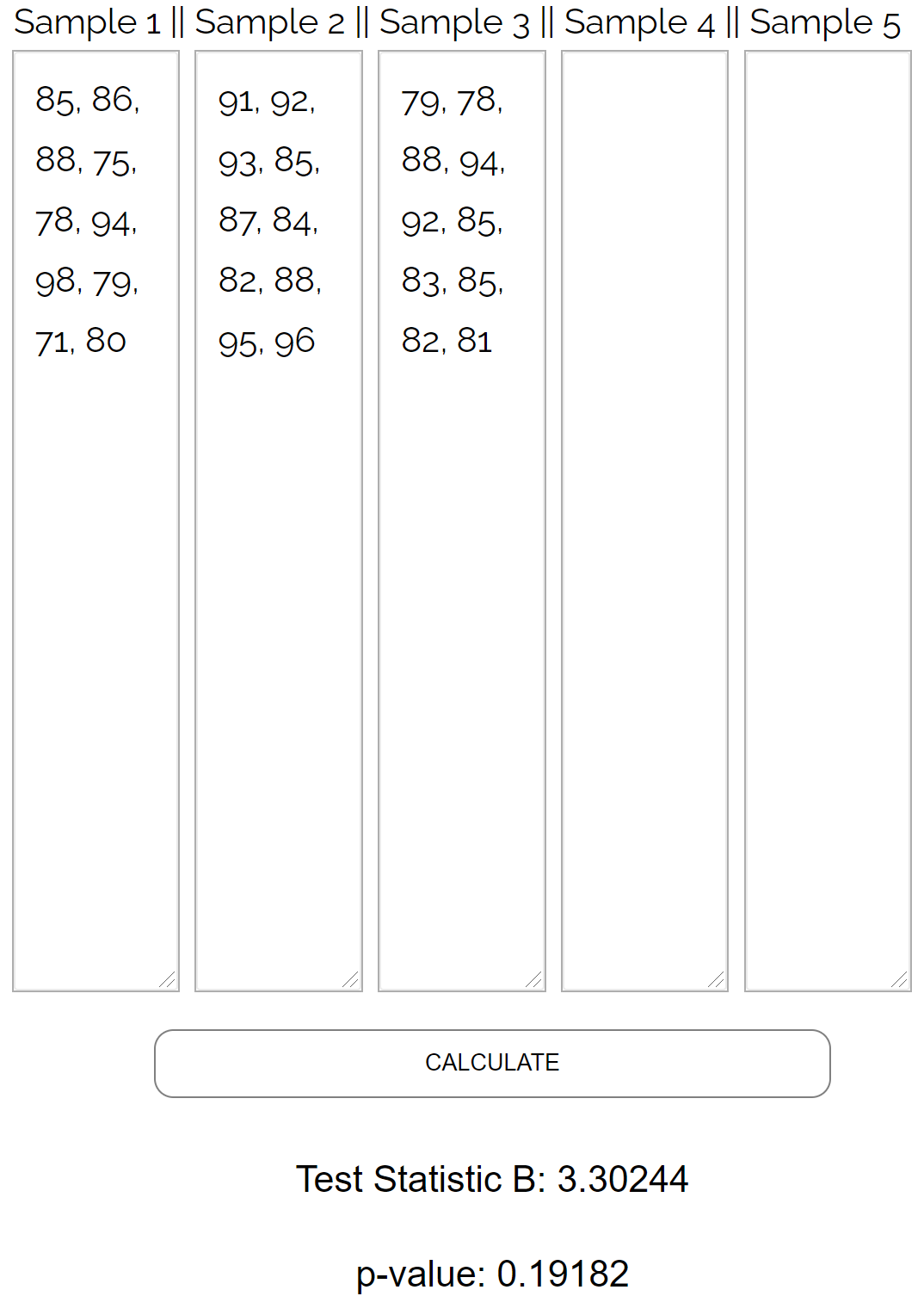
Тест дає такі результати:
- Статистика тесту B : 3,30244
- P-значення: 0,19182
Оскільки p-значення не менше 0,05, професору не вдасться відхилити нульову гіпотезу. Іншими словами, вона не має достатніх доказів, щоб стверджувати, що три групи мають різні прогалини.
Таким чином, вона може продовжити виконання одностороннього дисперсійного аналізу.
Додаткові ресурси
Як виконати тест Бартлетта в R (покроково)
Як виконати тест Бартлетта в Python (крок за кроком)