U-тест манна-уітні
U-критерій Манна-Уїтні (іноді його називають тестом рангової суми Вілкоксона) використовується для порівняння відмінностей між двома незалежними вибірками, коли вибіркові розподіли розподілені ненормально, а розміри вибірок невеликі (n < 30).
Він вважається непараметричним еквівалентом незалежного двовибіркового t-критерію .
Ось кілька прикладів того, коли можна використовувати U-тест Манна-Уітні:
- Ви хочете порівняти зарплати п’яти випускників університету А із зарплатами п’яти випускників університету Б. Зарплати не розподіляються зазвичай.
- Ви хочете знати, чи змінюється втрата ваги для двох груп: 12 осіб, які дотримуються дієти А, і 10 осіб, які дотримуються дієти Б. Втрата ваги не розподіляється нормально.
- Ви хочете знати, чи відрізняються бали 8 учнів класу А від балів 7 учнів класу Б. Бали розподілені ненормально.
У кожному прикладі ви хочете порівняти дві групи, розподіли вибірки не є нормальними, а розміри вибірки невеликі.
Таким чином, U-тест Манна-Уітні є прийнятним, якщо виконуються наступні припущення.
Припущення U тесту Манна-Уїтні
Перш ніж виконувати U-тест Манна-Уітні, ви повинні переконатися, що виконуються наступні чотири припущення:
- Звичайний або безперервний: змінна, яку ви аналізуєте, є порядковою або безперервною. Приклади порядкових змінних включають елементи Лайкерта (наприклад, 5-бальна шкала в діапазоні від «зовсім не згоден» до «повністю згоден»). Прикладами безперервних змінних є зріст (вимірюється в дюймах), вага (вимірюється у фунтах) або результати тестів (вимірюються від 0 до 100).
- Незалежність: усі спостереження обох груп незалежні одне від одного.
- Форма: форми розподілів для двох груп приблизно однакові.
Якщо ці припущення виконуються, ви можете виконати U-тест Манна-Уітні.
Як виконати U-тест Манна-Уітні
Щоб виконати U-тест Манна-Уітні, ми дотримуємося стандартної п’ятиетапної процедури перевірки гіпотези :
1. Сформулюйте припущення.
У більшості випадків U-тест Манна-Уітні виконується як двосторонній тест. Нульова та альтернативна гіпотези записуються у вигляді:
H 0 : Дві популяції рівні
H a : дві популяції не рівні
2. Визначте рівень значущості для використання гіпотези.
Визначтеся з рівнем значущості. Загальні варіанти: .01, .05 і .1.
3. Знайдіть статистику тесту.
Тестова статистика позначається U і є меншою з U 1 і U 2 , як визначено нижче:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
де n 1 і n 2 — розміри вибірки для зразків 1 і 2 відповідно, а R 1 і R 2 — сума рангів для зразків 1 і 2 відповідно.
Наведені нижче приклади детально покажуть, як знайти цю тестову статистику.
4. Відкинути або не відхилити нульову гіпотезу.
Використовуючи тестову статистику, визначте, чи можна відхилити нульову гіпотезу на основі рівня значущості та критичного значення, знайденого в U-таблиці Манна-Уітні.
5. Інтерпретуйте результати.
Інтерпретуйте результати тесту в контексті поставленого запитання.
Приклади виконання U-тесту Манна-Уітні
У наступних прикладах показано, як виконати U-тест Манна-Уїтні.
Приклад 1
Ми хочемо знати, чи ефективні нові ліки для запобігання нападам паніки. Загалом 12 пацієнтів випадковим чином розподіляють на дві групи по 6 осіб і отримують новий препарат або плацебо. Потім пацієнти записують кількість панічних атак, які вони зазнали протягом місяця.
Результати наведені нижче:
| НОВИЙ ПРЕПАРАТ | ПЛАЦЕБО |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Виконайте U-тест Манна-Уітні, щоб побачити, чи є різниця в кількості панічних атак серед пацієнтів у групі плацебо порівняно з групою нових препаратів. Використовуйте рівень значущості 0,05.
1. Сформулюйте припущення.
H 0 : Дві популяції рівні
H a : дві популяції не рівні
2. Визначте рівень значущості для використання гіпотези.
Проблема говорить нам, що ми повинні використовувати рівень значущості 0,05.
3. Знайдіть статистику тесту.
Нагадаємо, що тестова статистика позначається U і є меншою з U 1 і U 2 , як визначено нижче:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
де n 1 і n 2 — розміри вибірки для зразків 1 і 2 відповідно, а R 1 і R 2 — сума рангів для зразків 1 і 2 відповідно.
Щоб знайти R 1 і R 2 , нам потрібно об’єднати спостереження з обох груп і впорядкувати їх від найменшого до найбільшого:
| НОВИЙ ПРЕПАРАТ | ПЛАЦЕБО |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Загальна вибірка: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Ранги: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = сума рангів для зразка 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = сума рангів для зразка 2 = 1,5+3+6,5+10+11+12 = 44
Далі ми використовуємо наші розміри вибірки n 1 і n 2 , а також нашу рангову суму R 1 і R 2 , щоб знайти U 1 і U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Наша тестова статистика є меншою з U1 і U2 , яка дорівнює U=13.
Примітка: ми також можемо використати U-калькулятор Манна-Уїтні, щоб визначити, що U = 13.
4. Відкинути або не відхилити нульову гіпотезу.
Використовуючи n 1 = 6 і n 2 = 6 з рівнем значущості 0,05, U-таблиця Манна-Уітні говорить нам, що критичне значення дорівнює 5:
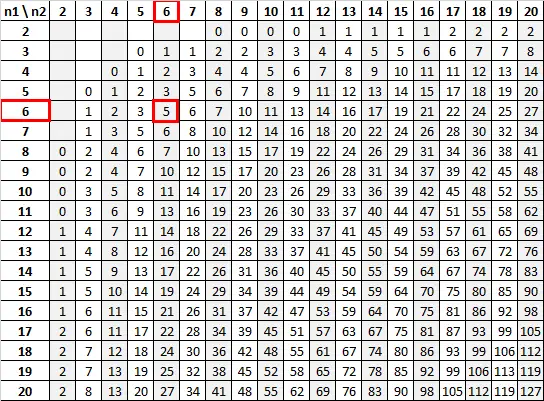
Оскільки наша тестова статистика (13) більша за наше критичне значення (5), ми не можемо відхилити нульову гіпотезу.
5. Інтерпретуйте результати.
Оскільки нам не вдалося відхилити нульову гіпотезу, у нас немає достатніх доказів, щоб стверджувати, що кількість панічних атак, які відчували пацієнти в групі плацебо, відрізняється від такої в групі нових препаратів.
Приклад 2
Ми хочемо знати, чи допомагає учням краще виконувати тестування 30-хвилинне навчання в день протягом тижня. Загалом 15 пацієнтів випадковим чином розподіляють у досліджувану групу або в жодну дослідницьку групу. Через тиждень усі учні складають той самий тест.
Результати тестування для обох груп наведено нижче:
| ВИВЧЕННЯ | БЕЗ ВИВЧЕННЯ |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Виконайте U-тест Манна-Уітні, щоб побачити, чи є різниця в результатах тесту для досліджуваної групи порівняно з групою, яка не вивчалася. Використовуйте рівень значущості 0,01.
1. Сформулюйте припущення.
H 0 : Дві популяції рівні
H a : дві популяції не рівні
2. Визначте рівень значущості для використання гіпотези.
Проблема говорить нам, що ми повинні використовувати рівень значущості 0,01.
3. Знайдіть статистику тесту.
Нагадаємо, що тестова статистика позначається U і є меншою з U 1 і U 2 , як визначено нижче:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
де n 1 і n 2 — розміри вибірки для зразків 1 і 2 відповідно, а R 1 і R 2 — сума рангів для зразків 1 і 2 відповідно.
Щоб знайти R 1 і R 2 , нам потрібно об’єднати спостереження з обох груп і впорядкувати їх від найменшого до найбільшого:
| ВИВЧЕННЯ | БЕЗ ВИВЧЕННЯ |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Загальна вибірка: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94, 95 , 96 , 99
Ряди: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = сума рангів для зразка 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = сума рангів для зразка 2 = 1+2+3+4+6+11+13 = 40
Далі ми використовуємо наші розміри вибірки n 1 і n 2 , а також нашу рангову суму R 1 і R 2 , щоб знайти U 1 і U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Наша тестова статистика є меншою з U1 і U2 , яка дорівнює U=12.
Примітка: ми також можемо використати U-калькулятор Манна-Уїтні, щоб визначити, що U = 12.
4. Відкинути або не відхилити нульову гіпотезу.
Використовуючи n 1 = 8 і n 2 = 7 з рівнем значущості 0,01, U-таблиця Манна-Уітні говорить нам, що критичне значення дорівнює 6:
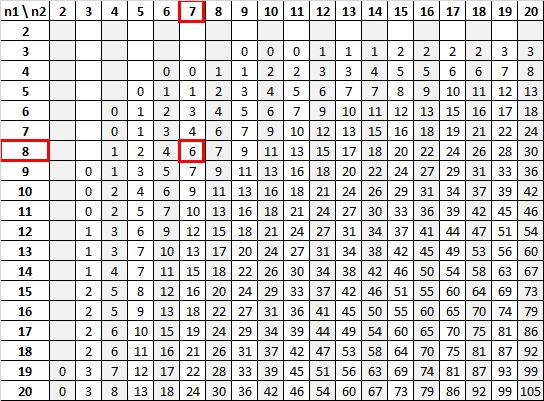
Оскільки наша тестова статистика (12) більша за наше критичне значення (6), ми не можемо відхилити нульову гіпотезу.
5. Інтерпретуйте результати.
Оскільки нам не вдалося відхилити нульову гіпотезу, у нас немає достатніх доказів того, що тестові результати студентів, які навчалися, відрізняються від результатів студентів, які не навчалися.
Додаткові ресурси
Калькулятор U-тесту Манна-Уітні
U-таблиця Манна-Уітні
Як виконати U-тест Манна-Уітні в Excel
Як виконати U-тест Манна-Уітні в R
Як виконати U-тест Манна-Уітні на Python
Як виконати U-тест Манна-Уітні в SPSS
Як виконати U-тест Манна-Уітні в Stata
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше