Як виконати тест на відсутність відповідності в r (покроково)

Тест на відсутність відповідності використовується, щоб визначити, чи забезпечує повна модель регресії значно кращу відповідність набору даних, ніж скорочена версія моделі.

Наприклад, скажімо, ми хочемо використати кількість вивчених годин , щоб передбачити результати іспитів для студентів певного коледжу. Ми можемо вирішити адаптувати наступні дві моделі регресії:

Повна модель: бал = β ₀ + B ₁ (годин) + B ₂ (годин) ²

Скорочена модель: оцінка = β ₀ + B ₁ (годин)

У наступному покроковому прикладі показано, як виконати тест на відсутність відповідності в R, щоб визначити, чи забезпечує повна модель значно кращу відповідність, ніж зменшена модель.

Крок 1: Створіть і візуалізуйте набір даних

По-перше, ми використаємо наступний код, щоб створити набір даних, який містить кількість вивчених годин і результати іспитів, отримані для 50 студентів:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Далі ми створимо діаграму розсіювання, щоб візуалізувати зв’язок між годинами та балом:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

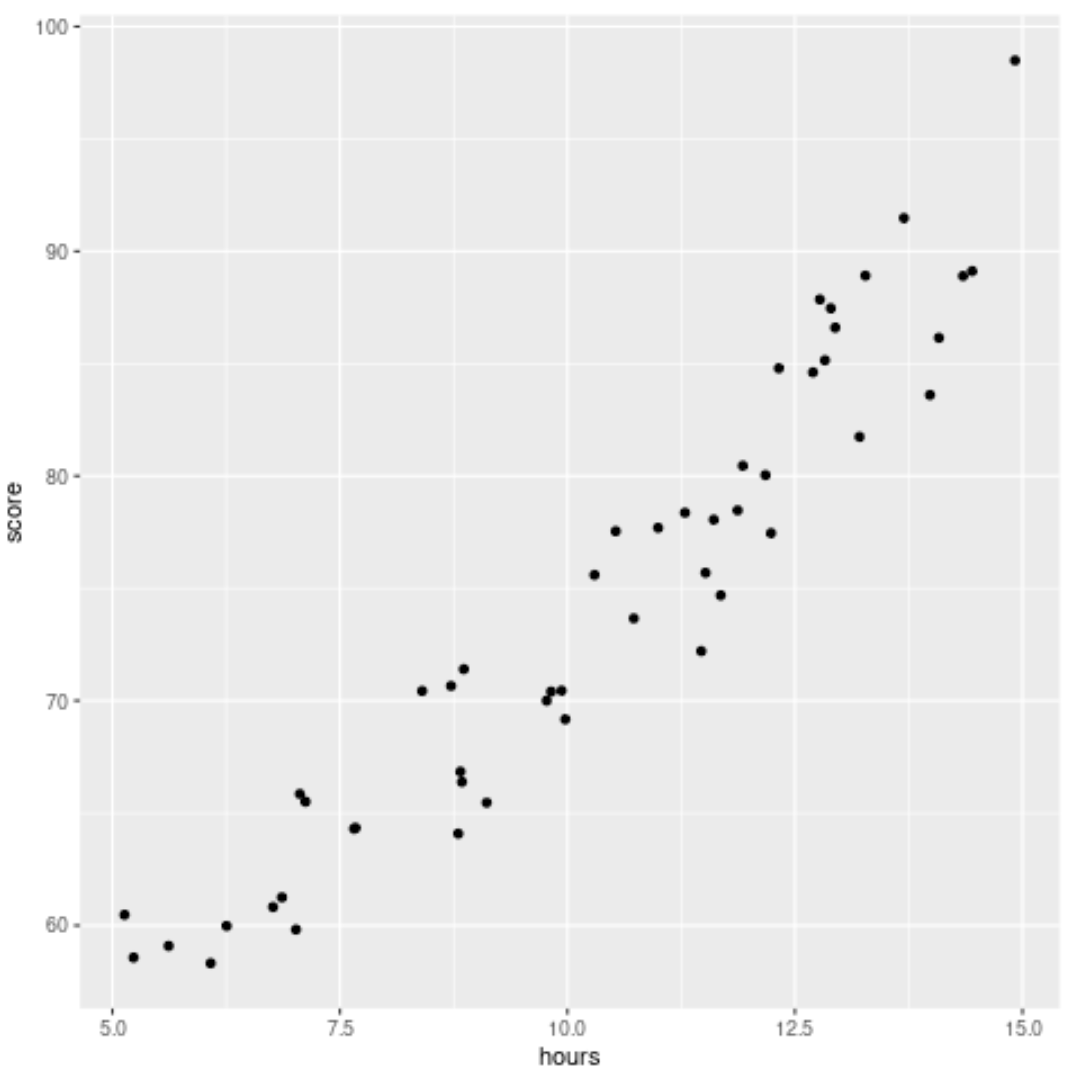
Крок 2. Підберіть дві різні моделі до набору даних

Далі ми підберемо дві різні моделі регресії до набору даних:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

Крок 3: Виконайте тест на відсутність відповідності

Далі ми використаємо команду anova() , щоб виконати перевірку відсутності відповідності між двома моделями:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Статистика тесту F дорівнює 10,554 , а відповідне значення p — 0,002144 . Оскільки це значення p менше 0,05, ми можемо відхилити нульову гіпотезу тесту та зробити висновок, що повна модель забезпечує статистично значуще кращу відповідність, ніж зменшена модель.

Крок 4: Візуалізуйте остаточну модель

Нарешті, ми можемо візуалізувати остаточну модель (повну модель) порівняно з вихідним набором даних:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

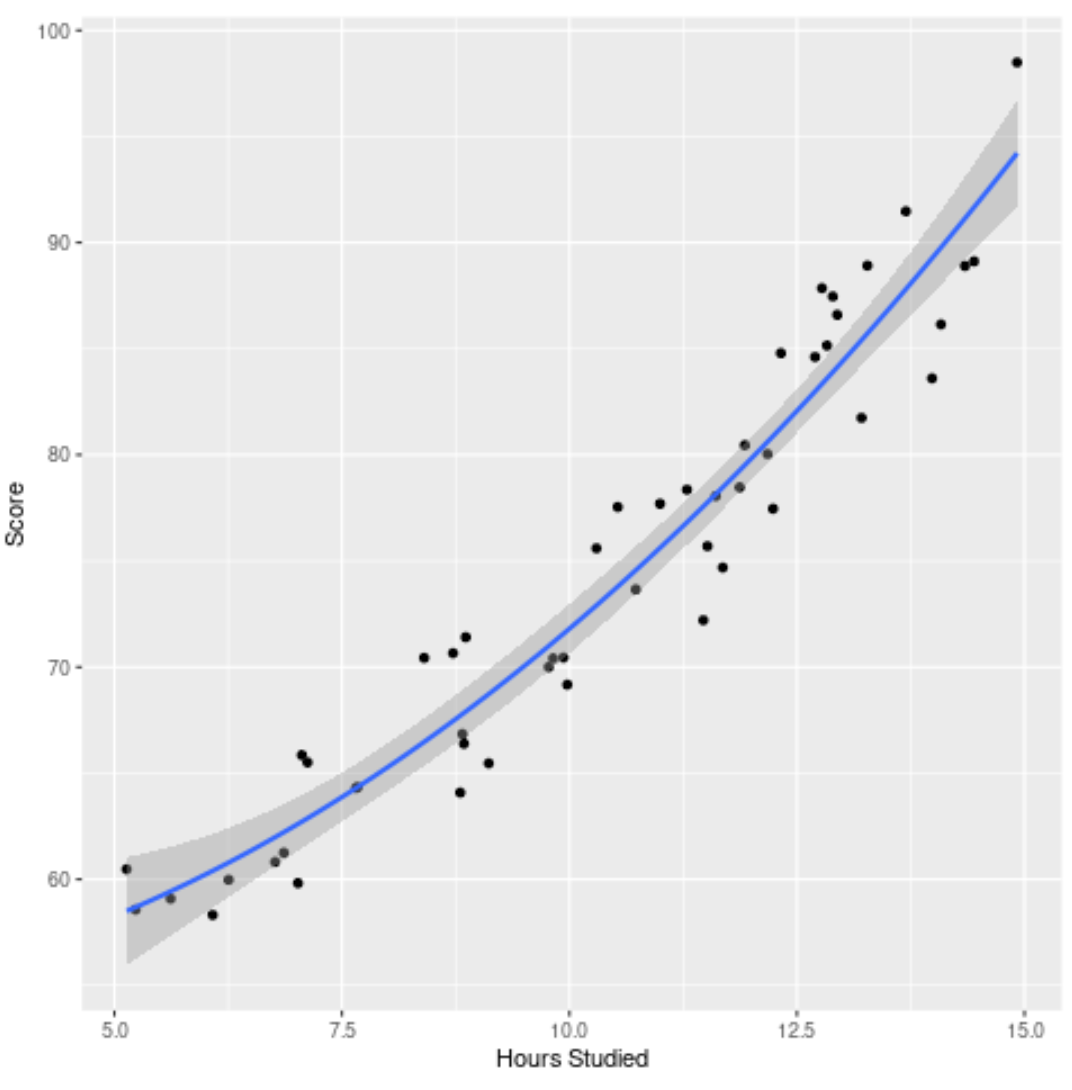
Ми бачимо, що крива моделі досить добре відповідає даним.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати поліноміальну регресію в R