Як виконати перевірку знакового рангу вілкоксона в r

Тест Wilcoxon Signed-Rank є непараметричною версією парного t-критерію . Він використовується, щоб перевірити, чи існує значна різниця між середніми значеннями двох сукупностей, коли розподіл відмінностей між двома вибірками не можна вважати нормальним.

У цьому підручнику пояснюється, як виконати перевірку рангів зі знаком Вілкоксона в R.

Приклад: Вілкоксон підписав ранговий тест у R

Припустимо, баскетбольний тренер хоче знати, чи певна тренувальна програма збільшує кількість штрафних кидків, які виконують його гравці. Щоб перевірити це, він попросив 15 гравців виконати по 20 штрафних кидків до і після програми тренувань.

Оскільки кожен гравець може бути «в парі» сам із собою, тренер планував використовувати парний t-тест, щоб визначити, чи є значна різниця між середньою кількістю штрафних кидків, виконаних до та після програми тренувань. навчання. Однак розподіл відмінностей виявляється ненормальним, тому замість цього тренер використовує тест Wilcoxon Signed-Rank.

У наступній таблиці представлено кількість штрафних кидків (з 20 спроб) кожним із 15 гравців до та після програми тренувань:

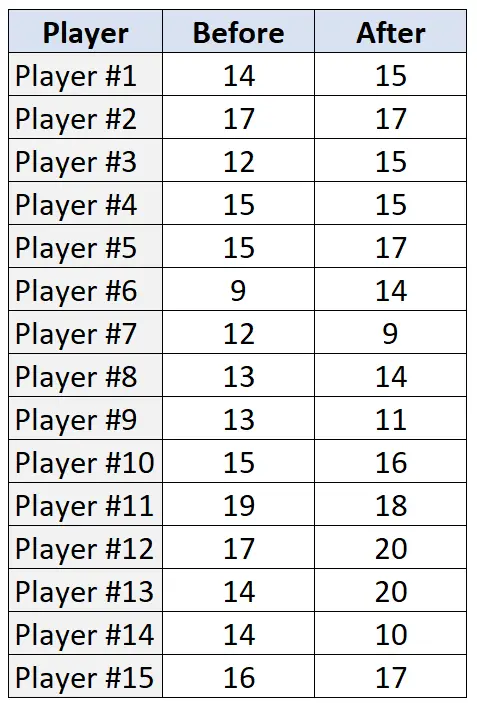
Щоб виконати тест Wilcoxon Signed-Rank для цих даних у R, ми можемо використати функцію wilcox.test() , яка використовує такий синтаксис:

wilcox.test(x, y, even = TRUE)

золото:

• x, y: два вектори значень даних
• paired: встановлення значення TRUE повідомляє R, що наші два вектори містили парні дані

Наступний код демонструє, як використовувати цю функцію для виконання тесту Wilcoxon Signed-Rank на цих даних:

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

Статистика тесту становить 29,5 , а відповідне значення p — 0,275 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. Не було статистично значущої різниці в кількості штрафних кидків до і після участі гравців у тренувальній програмі.

За замовчуванням ця функція виконує двосторонній тест Wilcoxon Signed-Rank, але ви можете вказати лівосторонній або правосторонній тест за допомогою альтернативного аргументу:

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Додаткові ресурси

Вступ до перевірки статусу Вілкоксона зі знаком
Калькулятор тесту з підписом Вілкоксона