Як перевірити нормальність у python (4 методи)

Багато статистичних тестів припускають , що набори даних розподілені нормально.

Є чотири поширені способи перевірити цю гіпотезу в Python:

1. (Наочний метод) Створіть гістограму.

• Якщо гістограма приблизно має форму дзвона, то дані вважаються нормально розподіленими.

2. (Візуальний метод) Створіть діаграму QQ.

• Якщо точки на графіку лежать приблизно вздовж прямої діагональної лінії, то дані вважаються нормально розподіленими.

3. (Формальний статистичний тест) Виконайте тест Шапіро-Вілка.

• Якщо p-значення тесту більше α = 0,05, то дані вважаються нормально розподіленими.

4. (Формальний статистичний тест) Виконайте критерій Колмогорова-Смирнова.

• Якщо p-значення тесту більше α = 0,05, то дані вважаються нормально розподіленими.

Наступні приклади показують, як використовувати кожен із цих методів на практиці.

Спосіб 1: Створення гістограми

У наступному коді показано, як створити гістограму для набору даних, який відповідає логарифмічному нормальному розподілу :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

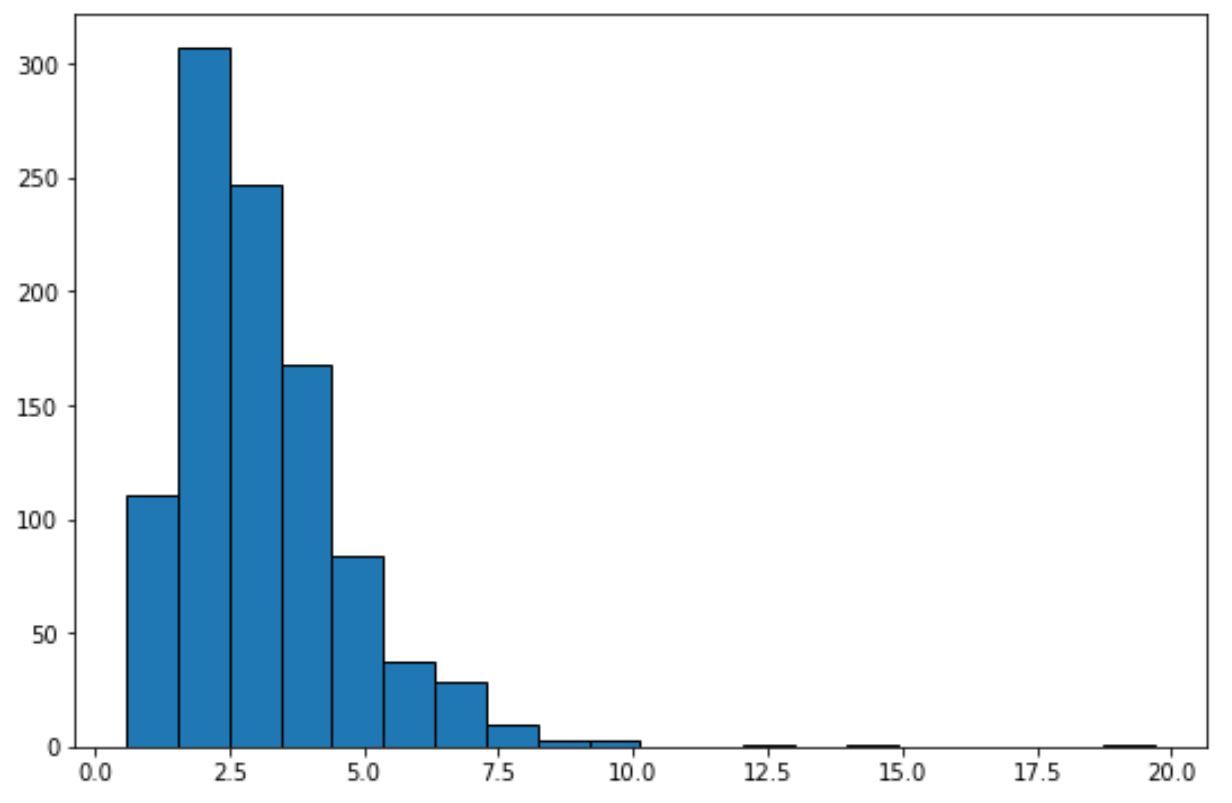
Просто подивившись на цю гістограму, ми можемо сказати, що набір даних не має «форми дзвона» і не розподілений нормально.

Спосіб 2: Створення графіка QQ

У наведеному нижче коді показано, як створити діаграму QQ для набору даних, який відповідає логарифмічно нормальному розподілу:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

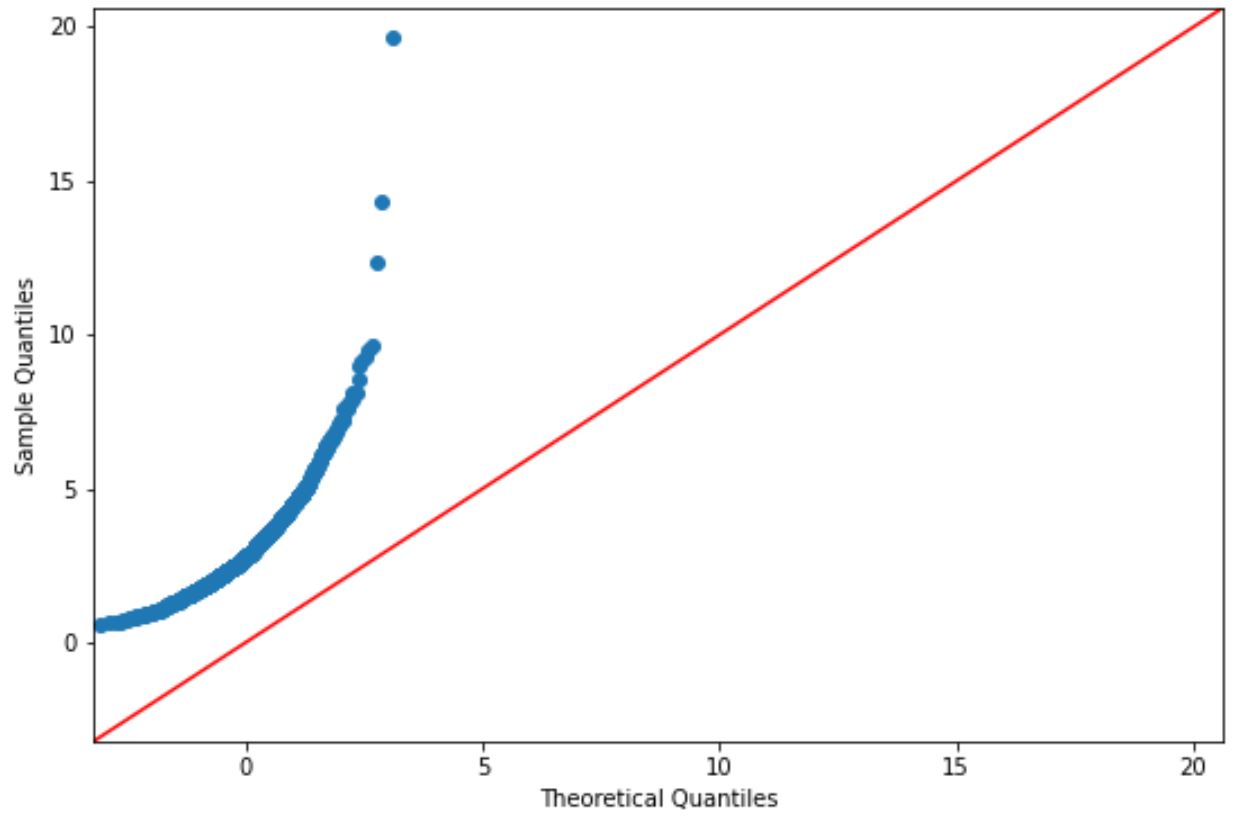
Якщо точки графіка лежать приблизно вздовж прямої діагональної лінії, ми зазвичай припускаємо, що набір даних розподілений нормально.

Однак точки на цьому графіку явно не відповідають червоній лінії, тому ми не можемо вважати, що цей набір даних розподілений нормально.

Це мало б мати сенс, враховуючи, що ми згенерували дані за допомогою функції логарифмічного нормального розподілу.

Спосіб 3: Виконайте тест Шапіро-Вілка

Наступний код показує, як виконати Шапіро-Вілк для набору даних, який відповідає логарифмічно-нормальному розподілу:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

З результату ми бачимо, що статистика тесту становить 0,857 , а відповідне значення p — 3,88e-29 (надзвичайно близьке до нуля).

Оскільки p-значення менше 0,05, ми відхиляємо нульову гіпотезу тесту Шапіро-Вілка.

Це означає, що ми маємо достатньо доказів, щоб стверджувати, що вибіркові дані не походять із нормального розподілу.

Спосіб 4: Виконайте тест Колмогорова-Смирнова

У наведеному нижче коді показано, як виконати перевірку Колмогорова-Смірнова для набору даних, який відповідає логарифмічному нормальному розподілу:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

З результату ми бачимо, що статистика тесту становить 0,841 , а відповідне значення p — 0,0 .

Оскільки p-значення менше 0,05, ми відхиляємо нульову гіпотезу критерію Колмогорова-Смирнова.

Це означає, що ми маємо достатньо доказів, щоб стверджувати, що вибіркові дані не походять із нормального розподілу.

Як обробляти нестандартні дані

Якщо заданий набір даних не розподілений нормально, ми часто можемо виконати одне з наступних перетворень, щоб зробити його більш нормально розподіленим:

1. Перетворення журналу: перетворення значень x в log(x) .

2. Перетворення квадратного кореня: перетворення значень x на √x .

3. Перетворення кубічного кореня: перетворення значень x на x ^1/3 .

Виконуючи ці перетворення, набір даних зазвичай стає більш нормально розподіленим.

Прочитайте цей посібник , щоб дізнатися, як виконати ці перетворення в Python.