Як трансформувати дані в python (лог, квадратний корінь, кубічний корінь)

Багато статистичних тестів припускають, що набори даних розподілені нормально. Однак на практиці це часто не так.

Одним із способів вирішення цієї проблеми є перетворення розподілу значень у наборі даних за допомогою одного з трьох перетворень:

1. Перетворення журналу: перетворення змінної відповіді з y на log(y) .

2. Перетворення квадратного кореня: перетворення змінної відповіді з y на √y .

3. Перетворення кубічного кореня: перетворення змінної відповіді з y на y ^1/3 .

Виконуючи ці перетворення, набір даних зазвичай стає більш нормально розподіленим.

У наступних прикладах показано, як виконати ці перетворення в Python.

Перетворення журналу в Python

У наведеному нижче коді показано, як виконати логарифмічне перетворення змінної та створити паралельні графіки для відображення вихідного розподілу та логарифмічного перетворення розподілу даних:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 4 , b= 15 , size= 300 )

#create log-transformed data
data_log = np. log (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Log-Transformed Data ')

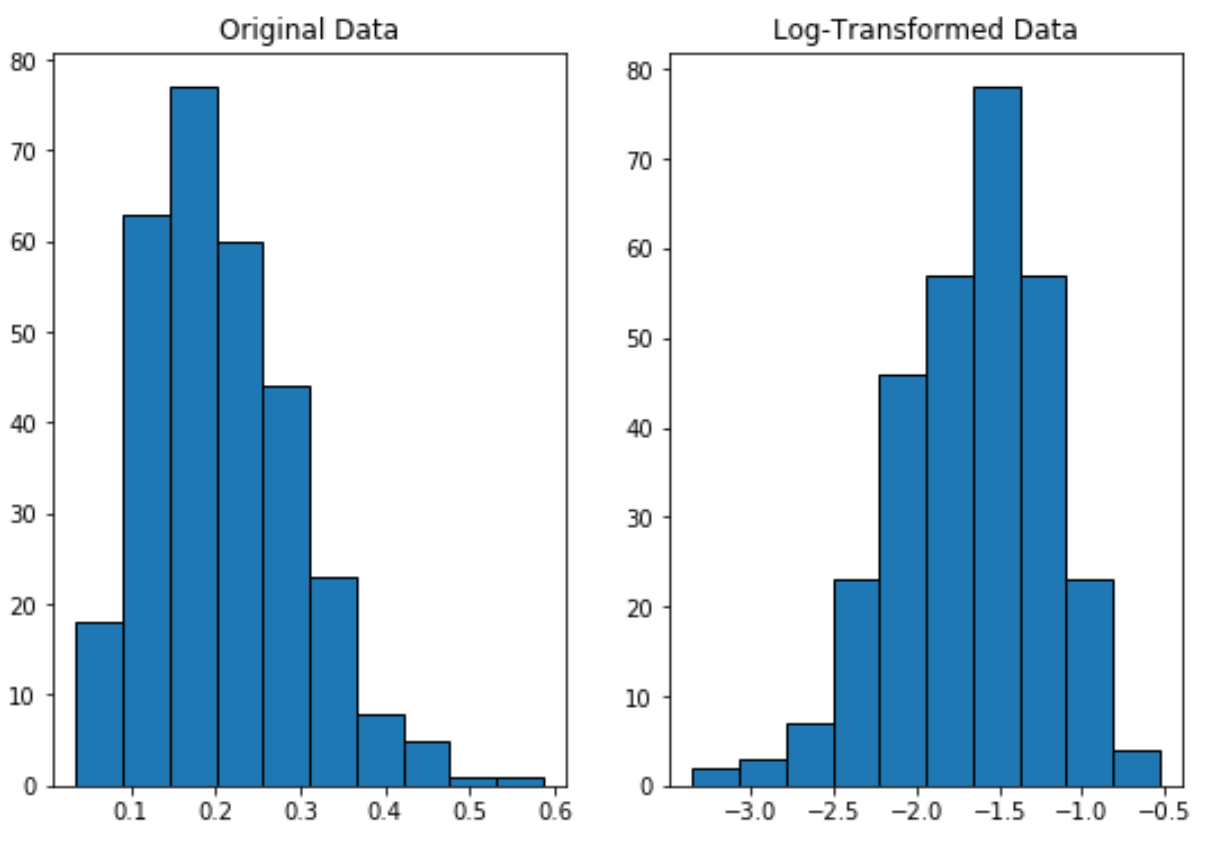
Зверніть увагу, що логарифмічно перетворений розподіл має більш нормальний розподіл, ніж вихідний розподіл.

Це все ще не ідеальна «форма дзвона», але вона ближча до нормального розподілу, ніж оригінальний розподіл.

Перетворення квадратного кореня в Python

У наведеному нижче коді показано, як виконати перетворення квадратного кореня для змінної та створити паралельні графіки для відображення вихідного розподілу та перетвореного квадратного кореня розподілу даних:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. sqrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Square Root Transformed Data ') 

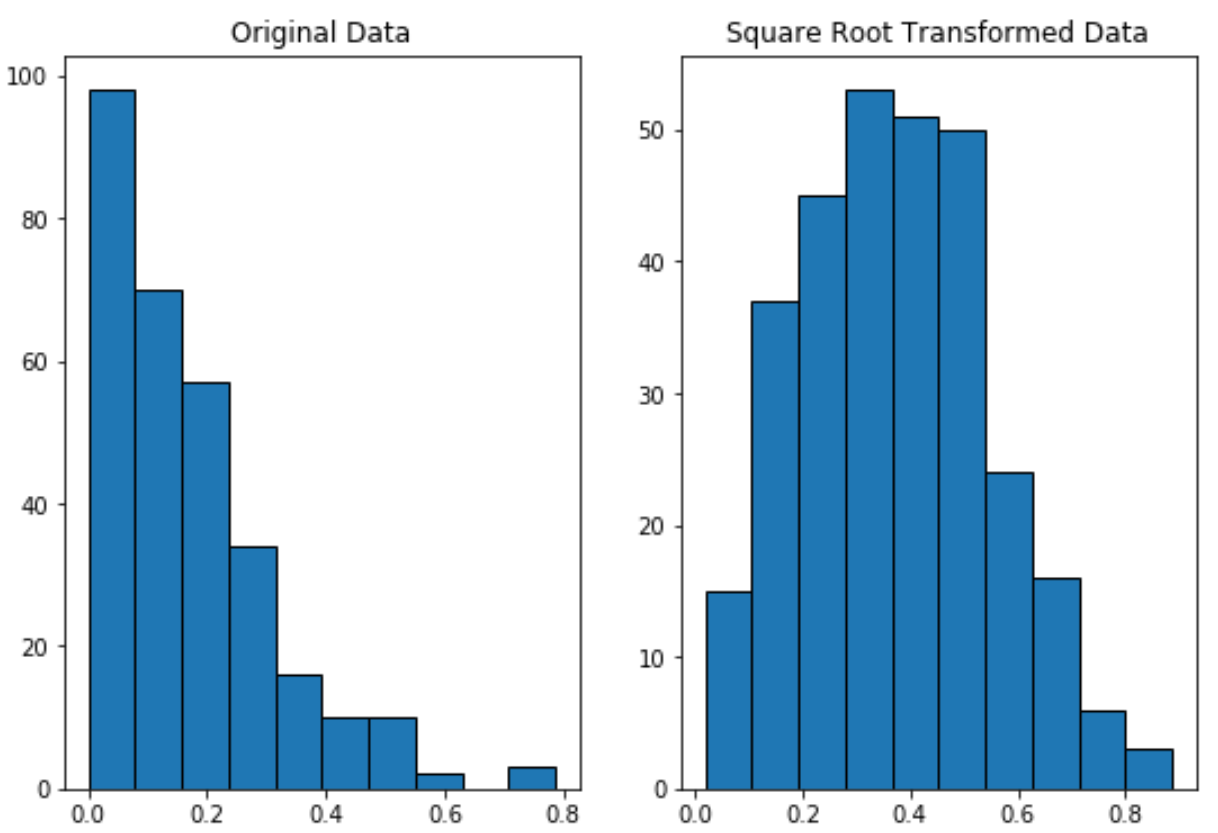
Зверніть увагу на те, що перетворені дані квадратного кореня розподілені набагато більш нормально, ніж вихідні дані.

Перетворення кубічного кореня в Python

У наведеному нижче коді показано, як виконати перетворення кубічного кореня для змінної та створити паралельні діаграми для відображення вихідного розподілу та перетвореного кубічного кореня розподілу даних:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. cbrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Cube Root Transformed Data ') 

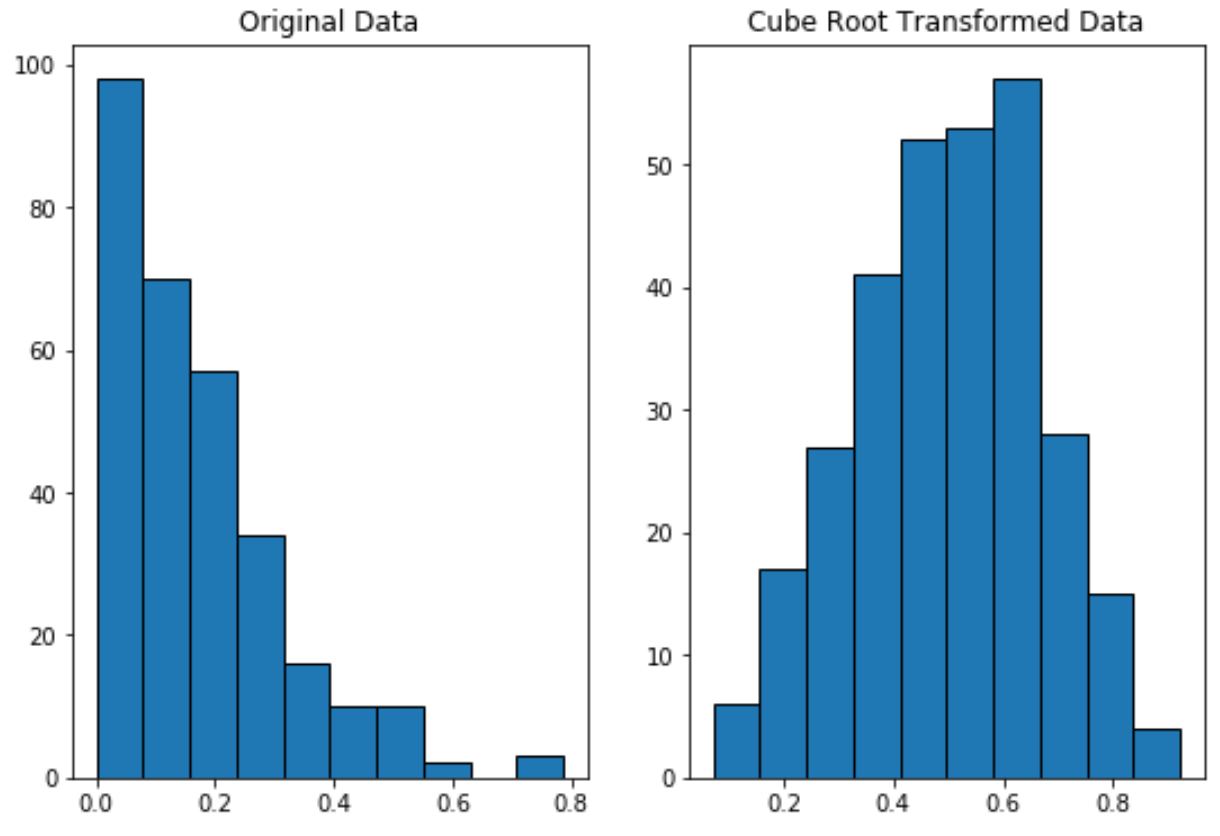
Зверніть увагу, як дані, перетворені за допомогою кубічного кореня, розподілені набагато більш нормально, ніж вихідні дані.

Додаткові ресурси

Як розрахувати Z-оцінки в Python
Як нормалізувати дані в Python
Що таке припущення нормальності в статистиці?