Вступ до трикутного розподілу

Трикутний розподіл — це неперервний розподіл ймовірностей із функцією щільності ймовірності у формі трикутника.

Він визначається трьома значеннями:

• Мінімальне значення має
• Максимальне значення b
• Максимальне значення c

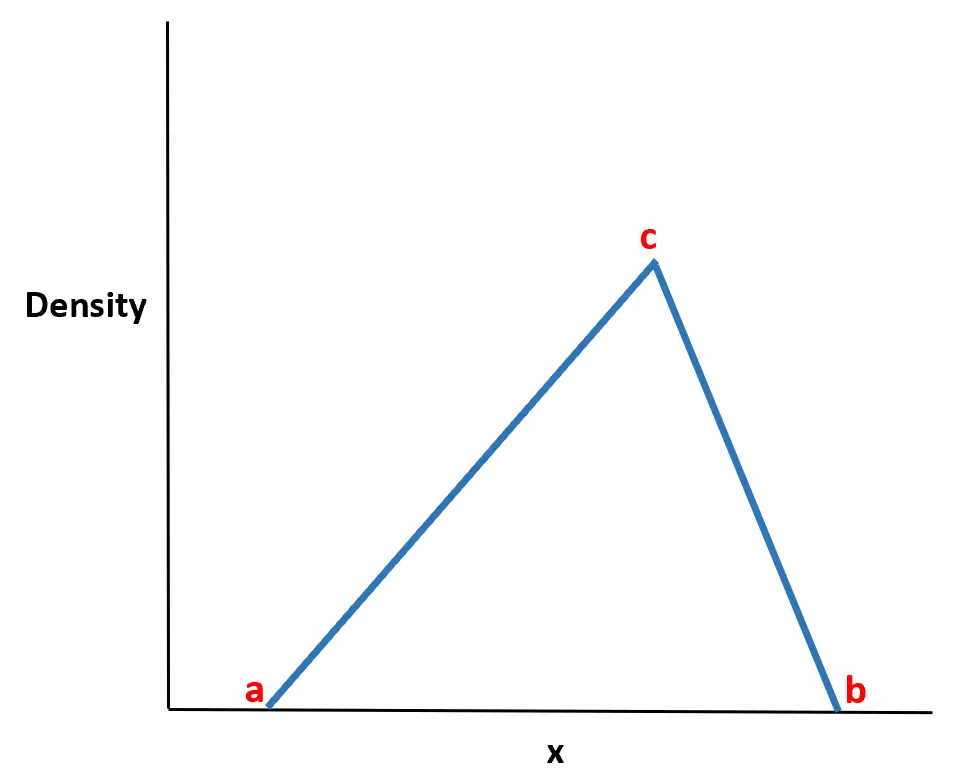
Назва розподілу походить від того, що функція щільності ймовірності має форму трикутника.

Виявляється, цей розподіл є надзвичайно корисним у реальному світі, тому що ми часто можемо оцінити мінімальне значення (a), максимальне значення (b) і, швидше за все, значення (c), які матиме випадкова змінна . часто може моделювати поведінку випадкових величин, використовуючи трикутний розподіл, знаючи лише ці три значення.

Наприклад, ресторан може оцінити, що його загальний обсяг продажів за наступний тиждень становитиме мінімум 10 000 доларів США, максимум 30 000 доларів США та, найімовірніше, 25 000 доларів США.

Використовуючи лише ці три числа, вони могли використовувати трикутний розподіл для визначення ймовірності здійснення певної кількості продажів.

Властивості трикутного розподілу

Трикутний розподіл має такі властивості:

PDF:

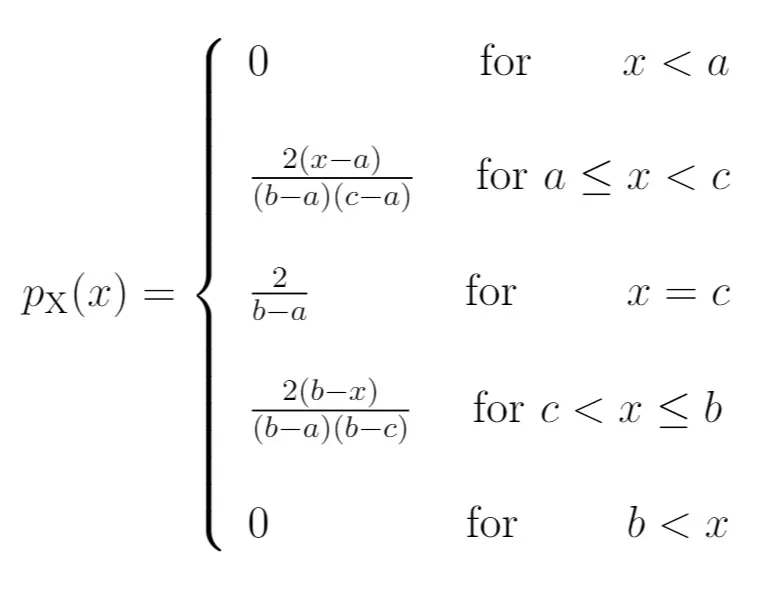
CDF:

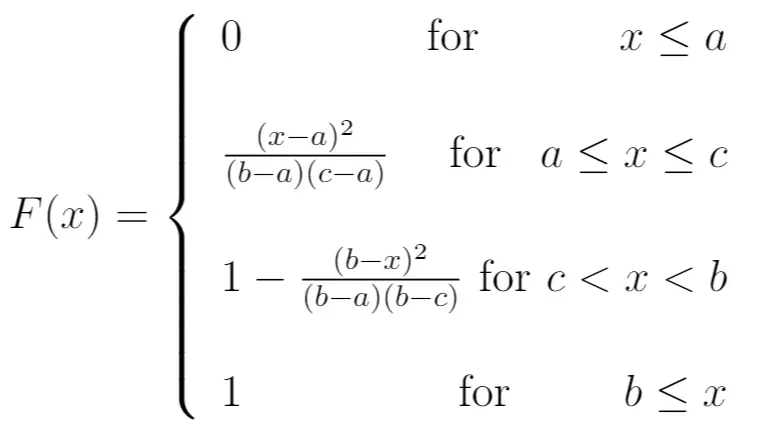
Середнє: (a + b + c) / 3

Режим: c

Дисперсія: (a ² + b ² + c ² – ab – ac – bc) / 18

Приклад використання трикутного розподілу

Повернемося до попереднього прикладу. Припустімо, ресторан оцінює, що його загальний обсяг продажів за наступний тиждень становитиме мінімум 10 000 доларів США, максимум 30 000 доларів США, а найімовірніше – 25 000 доларів США.

Яка ймовірність того, що загальний обсяг продажів ресторану менше 20 000 доларів?

Щоб відповісти на це запитання, ми можемо запитати x = загальний обсяг продажів. Ми знаємо, що x лежить між мінімальним значенням a в 10 000 доларів і максимальним значенням c в 25 000 доларів.

Отже, згідно з PDF-файлом, ми можемо використовувати таке рівняння, щоб знайти ймовірність того, що загальний обсяг продажів ресторану становить менше 20 000 доларів США:

• P(X < $20 000) = (xa) ² / ((ba)(ca))
• P(X < $20 000) = (20 000-10 000) ² / ((30 000-10 000)(25 000-10 000))
• P(X < $20 000) = 0,333

Імовірність того, що загальний обсяг продажів ресторану менше 20 000 доларів США, дорівнює 0,333 .

Який середній очікуваний обсяг продажів ресторану?

Ми можемо обчислити очікуваний середній обсяг продажів, використовуючи формулу для середнього значення, наведену раніше:

• Середнє = (a + b + c) / 3
• Середній = (10 000 $ + 30 000 $ + 25 000 $) / 3
• Середній = 21 667 доларів

Середній очікуваний обсяг продажів становить 21 667 .

Додаткові ресурси

Наступні навчальні посібники містять введення в інші часто використовувані дистрибутиви:

Нормальний розподіл
Біноміальний розподіл
Розподіл риби
Геометричний розподіл