Як використовувати трикутний розподіл у r (з прикладами)

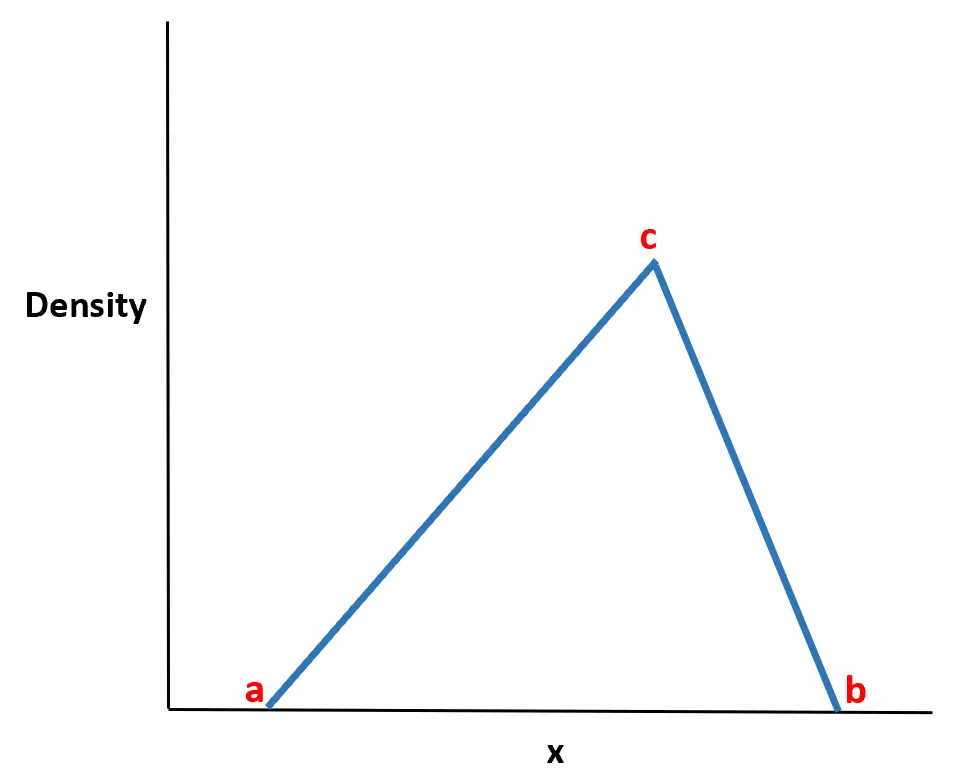
Трикутний розподіл — це неперервний розподіл ймовірностей із функцією щільності ймовірності у формі трикутника.

Він визначається трьома значеннями:

• Мінімальне значення має
• Максимальне значення b
• Максимальне значення c

Щоб обчислити ймовірності трикутного розподілу в R, ми можемо використати функцію ptri( ) із пакета EnvStats , яка використовує такий синтаксис:

ptri(q, min = 0, max = 1, mode = 1/2)

золото:

• q : цікавий квантиль
• min : мінімальне значення розподілу
• max : максимальне значення розподілу
• режим : Пікове значення розподілу

Наступні приклади показують, як використовувати цю функцію на практиці в R.

Приклад 1: обчислення ймовірності, меншої за певне значення

Припустімо, ресторан оцінює, що його загальний обсяг продажів за наступний тиждень становитиме мінімум 10 000 доларів США, максимум 30 000 доларів США, а найімовірніше – 25 000 доларів США.

Яка ймовірність того, що загальний обсяг продажів ресторану менше 20 000 доларів?

Щоб обчислити цю ймовірність, ми можемо використати такий код:

 library (EnvStats)

#calculate probability
ptri(q = 20000, min = 10000, max = 30000, mode = 25000)

[1] 0.3333333

Імовірність того, що загальний обсяг продажів ресторану менше 20 000 доларів США, дорівнює 0,333 .

Приклад 2: обчислення ймовірності, що перевищує певне значення

Скажімо, магазин розраховує, що кількість клієнтів, які прийдуть протягом певного тижня, становитиме мінімум 500, максимум 2000 і, швидше за все, 1200.

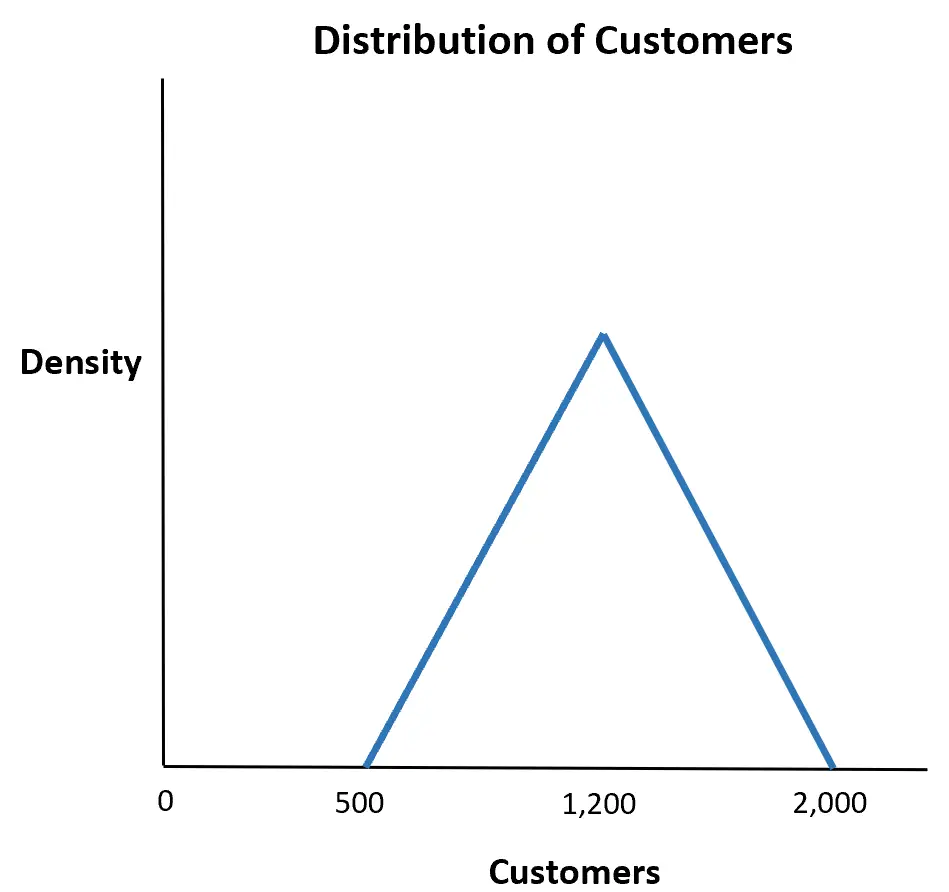
Яка ймовірність того, що більше 1500 покупців увійде до магазину протягом певного тижня?

Щоб обчислити цю ймовірність, ми можемо використати такий код:

 library (EnvStats)

#calculate probability
1 - ptri(q = 1500, min = 500, max = 2000, mode = 1200)

[1] 0.2083333

Імовірність того, що в магазин зайде більше 1500 покупців, дорівнює приблизно 0,208.

Примітка . Повну документацію щодо функції ptri() можна знайти тут .

Додаткові ресурси

У наступних посібниках пояснюється, як використовувати інші розподіли ймовірностей у R:

Як використовувати нормальний розподіл у R
Як використовувати біноміальний розподіл у R
Як використовувати розподіл Пуассона в R
Як використовувати мультиноміальний розподіл у R