Внутрішньогрупові або міжгрупові варіації в anova
Односторонній дисперсійний аналіз ANOVA використовується для визначення того, чи рівні середні три чи більше незалежних груп.
Односторонній ANOVA використовує такі нульові та альтернативні гіпотези :
- H 0 : Усі групові середні рівні.
- H A : Принаймні одне групове середнє значення відрізняється від інших.
Кожного разу, коли ви виконуєте односторонній дисперсійний аналіз, ви отримаєте зведену таблицю, яка виглядає так:
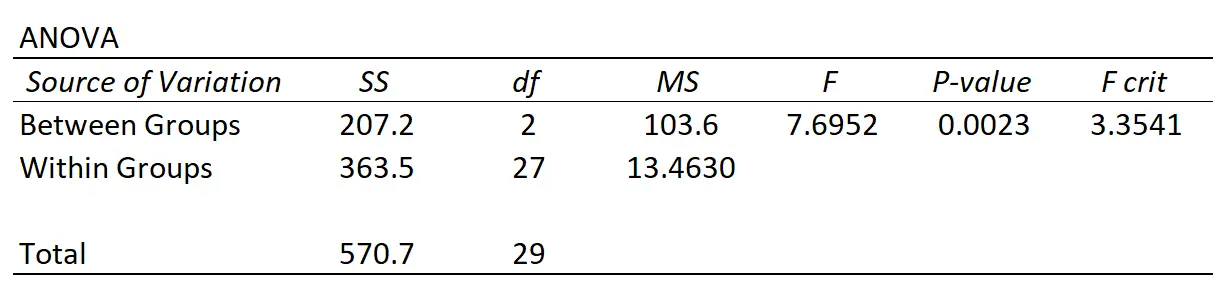
Ми бачимо, що дисперсійний аналіз вимірює два різних джерела варіації:
Варіація між групами : загальна варіація між середнім значенням кожної групи та загальним середнім.
Внутрішньогрупова варіація : загальна варіація індивідуальних значень у кожній групі та їхнє групове середнє значення.
Якщо варіація між групами є високою відносно варіації всередині групи, то F-статистика дисперсійного аналізу буде вищою, а відповідне значення p – нижчим, що підвищує ймовірність того, що нульову гіпотезу буде відхилено, згідно з якою групові середні рівні.
У наступному прикладі показано, як на практиці обчислити варіацію між групами та варіацію всередині групи для одностороннього дисперсійного аналізу.
Приклад: обчислення варіації всередині групи та між групами в ANOVA
Припустімо, ми хочемо визначити, чи призводять три різні методи навчання до різних середніх балів за іспит. Щоб перевірити це, ми набираємо 30 студентів і випадковим чином призначаємо по 10 для використання іншого методу навчання.
Результати іспитів студентів у кожній групі наведені нижче:
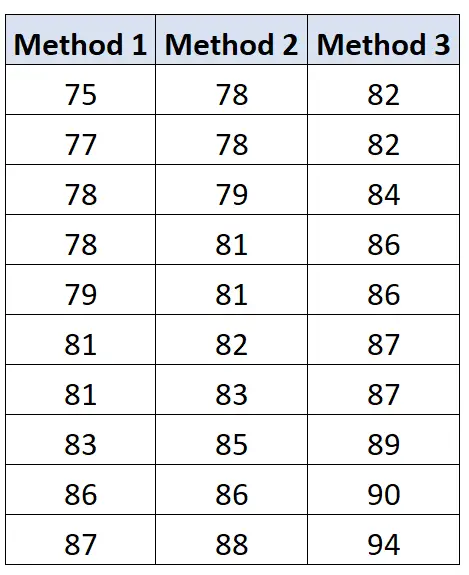
Ми можемо використати наступну формулу для розрахунку варіації між групами :
Варіація між групами = Σn j (X j – X ..) 2
золото:
- n j : розмір вибірки групи j
- Σ : символ, що означає «сума»
- X j : середнє значення групи j
- X .. : загальне середнє
Щоб обчислити це значення, ми спочатку обчислимо середнє для кожної групи та загальне середнє:
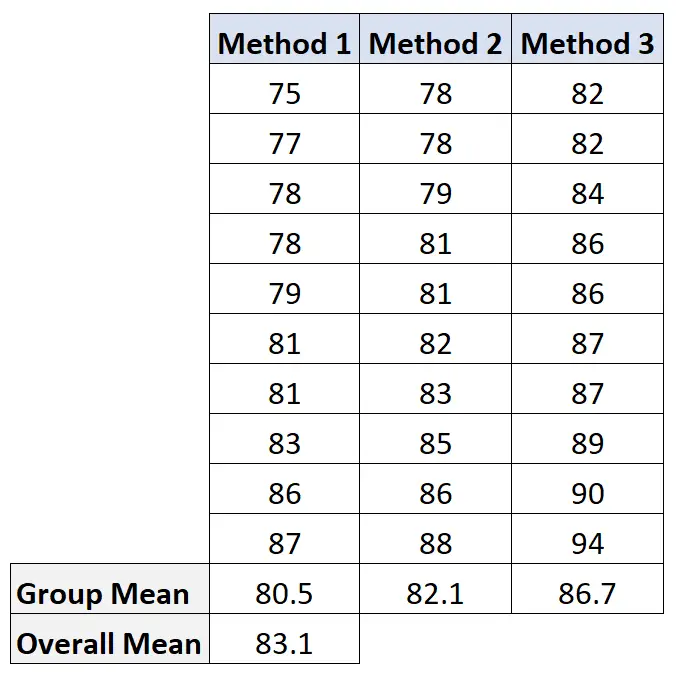
Потім ми обчислюємо варіацію між групами таким чином: 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Тоді ми можемо використати наступну формулу для розрахунку варіації всередині групи :
Внутрішньогрупова варіація : Σ(X ij – X j ) 2
золото:
- Σ : символ, що означає «сума»
- X ij : i-те спостереження групи j
- X j : середнє значення групи j
У нашому прикладі ми обчислюємо варіацію всередині групи як:
1 група: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2 + (78-80,5) 2 + (79-80,5) 2 + (81-80,5) 2 + (81-80,5) 2 + (83-80,5) 2 + (86-80,5) 2 + (87-80,5) 2 = 136,5
2 група: (78-82,1) 2 + (78-82,1) 2 + (79-82,1) 2 + (81-82,1) 2 + (81-82,1) 2 + (82-82,1) 2 + (83-82,1) 2 + (85-82,1) 2 + (86-82,1) 2 + (88-82,1) 2 = 104,9
3 група: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2 + (86-86,7) 2 + (86-86,7) 2 + (87-86,7) 2 + (87-86,7) 2 + (89-86,7) 2 + (90-86,7) 2 + (94-86,7) 2 = 122,1
Варіація всередині групи: 136,5 + 104,9 + 122,1 = 363,5
Якщо ми використовуємо статистичне програмне забезпечення для виконання одностороннього дисперсійного аналізу за допомогою цього набору даних, ми отримаємо таку таблицю дисперсійного аналізу:
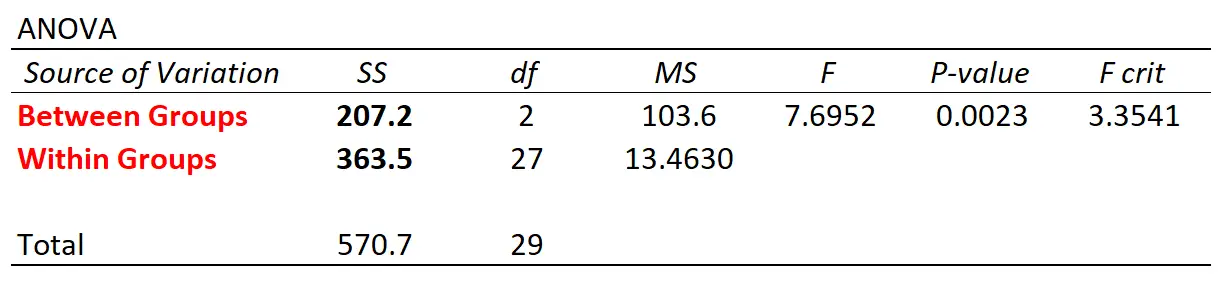
Зверніть увагу, що міжгрупові та внутрішньогрупові значення варіації збігаються з тими, які ми розрахували вручну.
Загальна F-статистика в таблиці є способом кількісної оцінки зв’язку між варіаціями між групами та варіаціями всередині групи.
Чим більша статистика F, тим більша варіація середніх значень між групами порівняно з варіацією всередині груп.
Отже, чим більше F-статистика, тим очевидніше, що існує різниця між груповими середніми.
У цьому прикладі ми бачимо, що p-значення, яке відповідає F-статистиці 7,6952, становить 0,0023 .
Оскільки це значення менше α = 0,05, ми відхиляємо нульову гіпотезу дисперсійного аналізу та робимо висновок, що три методи дослідження не призводять до однакових балів на іспиті.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про моделі ANOVA:
Вступ до одностороннього дисперсійного аналізу
Як інтерпретувати значення F і P у ANOVA
Повний посібник: як звітувати про результати ANOVA
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше