Повний посібник: факторний дизайн 2×3

Факторний план 2 × 3 — це тип експериментального плану, який дозволяє дослідникам зрозуміти вплив двох незалежних змінних на одну залежну змінну.

У цьому типі дизайну одна незалежна змінна має два рівні , а інша незалежна змінна має три рівні.

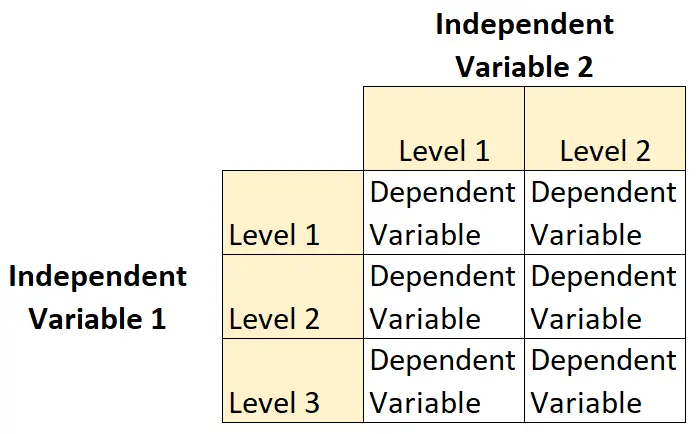
Наприклад, припустімо, що ботанік хоче зрозуміти вплив сонячного світла (низького, середнього або сильного) і частоти поливу (щодня чи щотижня) на ріст певного виду рослин.

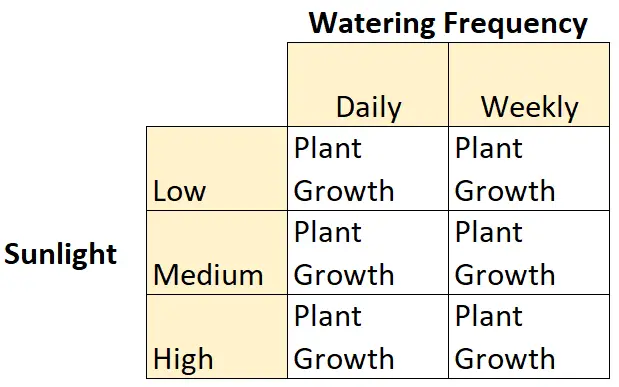
Це приклад факторіального плану 2 × 3, оскільки є дві незалежні змінні, одна з двома рівнями, а друга з трьома рівнями:

• Незалежна змінна №1: сонячне світло
  • Рівні: низький, середній, високий
• Незалежна змінна №2: частота поливу
  • Рівні: щоденний, тижневий

І є залежна змінна: ріст рослин.

Мета факторного дизайну 2 × 3

Факторний план 2×3 дозволяє аналізувати такі ефекти:

Основні ефекти: це вплив окремої незалежної змінної на залежну змінну.

Наприклад, у нашому попередньому сценарії ми могли б проаналізувати такі основні ефекти:

• Основний вплив сонячного світла на ріст рослин.
  • Середній ріст усіх рослин, які отримували мало сонячного світла.
  • Середній ріст усіх рослин, які отримували середнє сонячне світло.
  • Середній ріст усіх рослин, які отримали високе сонячне освітлення.
• Основний вплив частоти поливу на ріст рослин.
  • Середній ріст усіх рослин, що поливали щодня.
  • Середній ріст усіх рослин, які поливали щотижня.

Ефекти взаємодії: вони виникають, коли вплив однієї незалежної змінної на залежну змінну залежить від рівня іншої незалежної змінної.

Наприклад, у нашому попередньому сценарії ми могли б проаналізувати такі ефекти взаємодії:

• Чи залежить вплив сонячного світла на ріст рослин від частоти поливу?
• Чи залежить вплив частоти поливу на ріст рослин від сонячного світла?

Як аналізувати факторний план 2 × 3

Ми можемо виконати двосторонній дисперсійний аналіз , щоб офіційно перевірити, чи мають незалежні змінні статистично значущий зв’язок із залежною змінною.

Наприклад, наступний код показує, як виконати двосторонній дисперсійний аналіз для нашого гіпотетичного заводського сценарію в R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' Low ', ' Medium ', ' High '), each = 15, times = 2),
                 water = rep(c(' Daily ', ' Weekly '), each = 45, times = 2),
                 growth = c(rnorm(15, 9, 2), rnorm(15, 10, 3), rnorm(15, 13, 2),
                            rnorm(15, 8, 3), rnorm(15, 10, 4), rnorm(15, 12, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 2 602.3 301.15 50.811 <2e-16 ***
water 1 39.6 39.62 6.685 0.0105 *  
sunlight:water 2 15.1 7.56 1.275 0.2819    
Residuals 174 1031.3 5.93                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ось як інтерпретувати результат ANOVA:

• P-значення, пов’язане з сонячним світлом, становить <2e-16 . Оскільки це число менше 0,05, це означає, що вплив сонячного світла має статистично значущий вплив на ріст рослин.
• P-значення, пов’язане з водою, становить 0,0105 . Оскільки цей показник менше 0,05, це означає, що частота поливу також має статистично значущий вплив на ріст рослин.
• P-значення взаємодії між сонячним світлом і водою становить 0,2819 . Оскільки цей показник не менше 0,05, це означає відсутність ефекту взаємодії між сонячним світлом і водою.

Додаткові ресурси

Наступні навчальні посібники надають додаткову інформацію про дизайн експерименту та аналіз:

Повний посібник: факторний дизайн 2 × 2
Що таке рівні незалежної змінної?
Незалежні або залежні змінні
Що таке факторний дисперсійний аналіз?