Як використовувати фіктивні змінні в регресійному аналізі

Лінійна регресія – це метод, який ми можемо використати для кількісного визначення зв’язку між однією або декількома змінними предиктора та змінною відповіді .

Зазвичай ми використовуємо лінійну регресію з кількісними змінними . Іноді їх називають «числовими» змінними, це змінні, які представляють величину, яку можна виміряти. Приклади:

• Кількість квадратних метрів в будинку
• Чисельність населення міста
• Вік особини

Однак іноді ми хочемо використовувати категоріальні змінні як змінні-прогнози. Це змінні, які приймають імена або мітки та можуть потрапити в категорії. Приклади:

• Колір очей (наприклад, «блакитні», «зелені», «карі»)
• Стать (наприклад, «чоловік», «жінка»)
• Сімейний стан (наприклад, «одружений», «неодружений», «розлучений»)

Використовуючи категоріальні змінні, немає сенсу просто призначати такі значення, як 1, 2, 3, таким значенням, як «синій», «зелений» і «коричневий», оскільки немає сенсу говорити що зелений подвійний . такий барвистий, як синій чи коричневий, утричі барвистіший за синій.

Замість цього рішення полягає у використанні фіктивних змінних . Це змінні, які ми створюємо спеціально для регресійного аналізу і які приймають одне з двох значень: нуль або одиницю.

Фіктивні змінні: числові змінні, які використовуються в регресійному аналізі для представлення категоріальних даних, які можуть приймати лише одне з двох значень: нуль або одиницю.

Кількість фіктивних змінних, які нам потрібно створити, дорівнює k -1, де k — кількість різних значень, які може приймати категоріальна змінна.

Наступні приклади ілюструють, як створити фіктивні змінні для різних наборів даних.

Приклад 1. Створіть фіктивну змінну лише з двома значеннями

Припустімо, що ми маємо такий набір даних і хочемо використовувати стать і вік для прогнозування доходу :

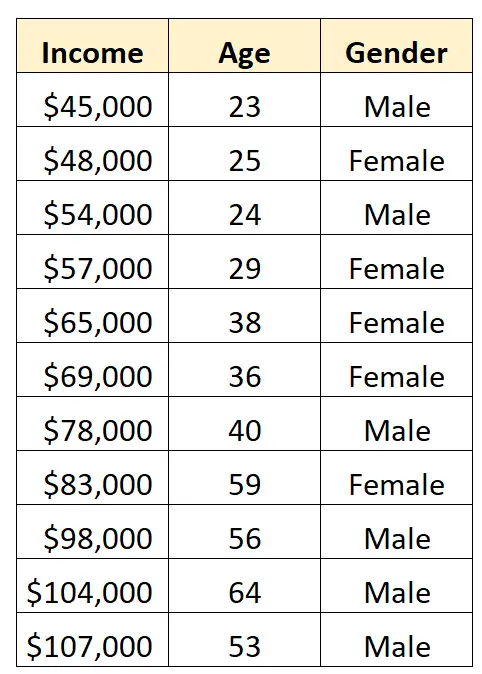
Щоб використовувати стать як прогностичну змінну в регресійній моделі, нам потрібно перетворити її на фіктивну змінну.

Оскільки наразі це категоріальна змінна, яка може приймати два різних значення («Чоловік» або «Жінка»), ми просто створюємо k -1 = 2-1 = 1 фіктивну змінну.

Щоб створити цю фіктивну змінну, ми можемо вибрати одне зі значень («Чоловічий» або «Жіночий»), щоб представляти 0, а інше — 1.

Загалом ми зазвичай представляємо найпоширеніше значення 0, що буде «чоловічим» у цьому наборі даних.

Отже, ось як перетворити стать у фіктивну змінну:

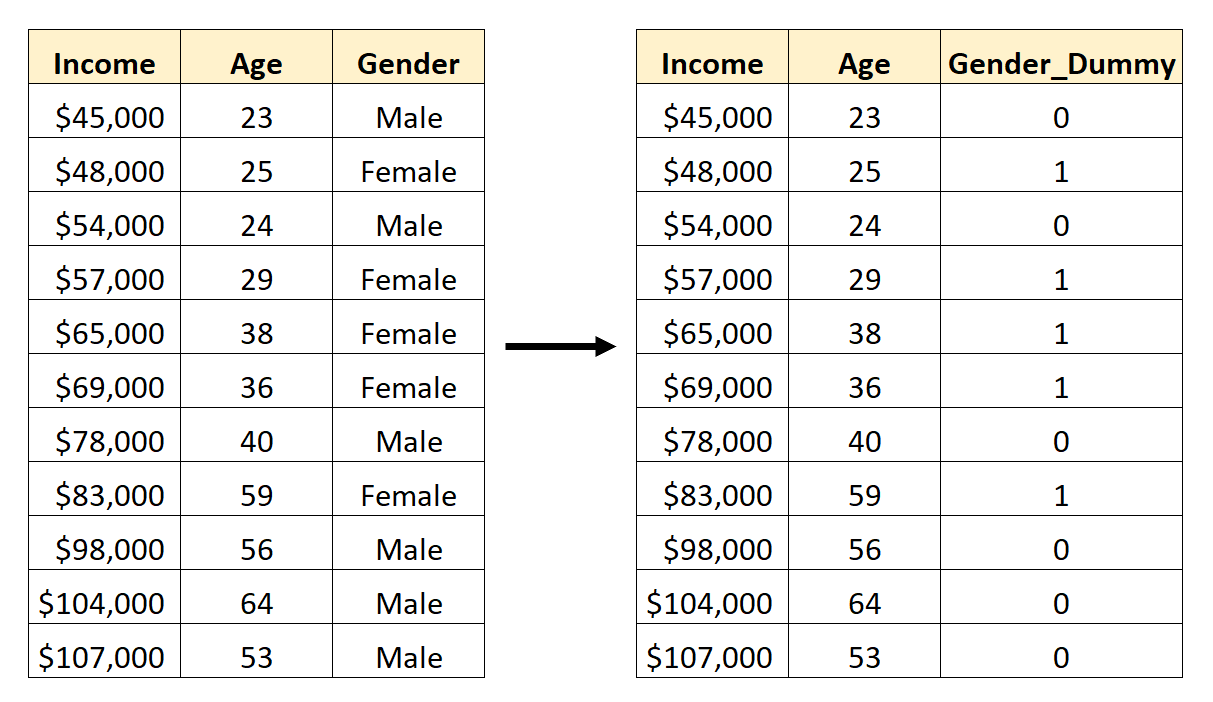
Тоді ми могли б використовувати Age і Gender_Dummy як змінні предиктора в регресійній моделі.

Приклад 2: Створення фіктивної змінної з кількома значеннями

Припустімо, ми маємо такий набір даних і хочемо використовувати сімейний стан і вік для прогнозування доходу :

Щоб використовувати сімейний стан як змінну прогнозу в регресійній моделі, нам потрібно перетворити його на фіктивну змінну.

Оскільки наразі це категоріальна змінна, яка може приймати три різні значення («Одружений», «Одружений» або «Розлучений»), нам потрібно створити k -1 = 3-1 = 2 фіктивні змінні.

Щоб створити цю фіктивну змінну, ми можемо залишити «Single» як базове значення, оскільки воно з’являється найчастіше. Отже, ось як ми перетворимо сімейний стан у фіктивні змінні:

Потім ми могли б використовувати Вік , Одружений і Розлучений як змінні прогнозу в регресійній моделі.

Як інтерпретувати результати регресії з фіктивними змінними

Припустімо, що ми адаптуємо модель множинної лінійної регресії , використовуючи набір даних із попереднього прикладу з віком , одруженим і розлученим як змінними предикторами та доходом як змінною відповіді.

Ось результат регресії:

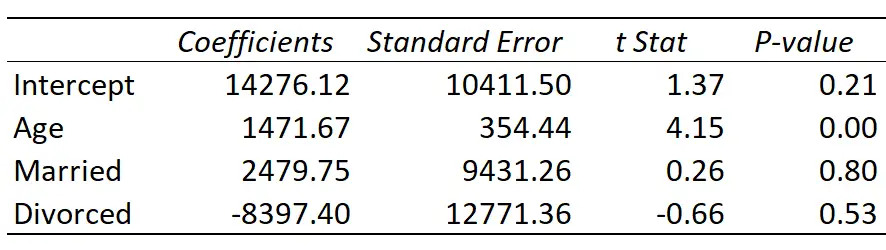
Підібрана лінія регресії визначається як:

Дохід = 14 276,21 + 1 471,67*(вік) + 2 479,75*(одружений) – 8 397,40*(розлучений)

Ми можемо використати це рівняння, щоб визначити приблизний дохід людини на основі її віку та сімейного стану. Наприклад, особа у віці 35 років і одружена матиме орієнтовний дохід у 68 264 долари :

Дохід = 14 276,21 + 1 471,67*(35) + 2 479,75*(1) – 8 397,40*(0) = 68 264 доларів США

Ось як інтерпретувати коефіцієнти регресії в таблиці:

• Відрізок: відрізок являє собою середній дохід самотньої людини у віці нуля. Очевидно, що ви не можете мати нульові роки, тому немає сенсу інтерпретувати перехоплення саме по собі в цій конкретній моделі регресії.
• Вік: кожен рік збільшення віку пов’язаний із середнім зростанням доходу на 1471,67 доларів США. Оскільки p-значення (0,00) менше 0,05, вік є статистично значущим предиктором доходу.
• Одружений: одружений заробляє в середньому на 2479,75 доларів США більше, ніж неодружений. Оскільки р-значення (0,80) не менше 0,05, ця різниця не є статистично значущою.
• Розлучений: розлучена особа заробляє в середньому на 8397,40 доларів США менше, ніж неодружена особа. Оскільки р-значення (0,53) не менше 0,05, ця різниця не є статистично значущою.

Оскільки обидві фіктивні змінні не були статистично значущими, ми могли вилучити сімейний стан як предиктор із моделі, оскільки він, здається, не додає прогностичного значення доходу.

Додаткові ресурси

Якісні та кількісні змінні
Пастка фіктивної змінної
Як читати та інтерпретувати таблицю регресії
Пояснення значень P і статистичної значущості