Що вважається хорошою чи поганою залишковою ділянкою?
У регресійному аналізі графік залишків — це тип графіка, який відображає підібрані значення регресійної моделі на осі X і залишки моделі вздовж осі Y.
Під час візуальної перевірки залишкового макета ми зазвичай шукаємо дві речі, щоб визначити, чи є макет «хорошим» чи «поганим»:
1. Чи демонструють залишки чітку тенденцію?
- На «хорошому» графіку залишків залишки не демонструють чіткої тенденції.
- На «поганому» залишковому графіку залишки мають певний тип шаблону, наприклад криву або хвилю. Це вказує на те, що регресійна модель, яку ми використали, не забезпечує належної відповідності даним.
2. Залишки систематично збільшують або зменшують дисперсію?
- На «хорошому» графіку залишків залишки випадковим чином розкидані навколо нуля без систематичного збільшення або зменшення дисперсії.
- На «поганому» графіку залишків дисперсія залишків систематично збільшується або зменшується.
Якщо залишковий графік оцінюється як «добре», це означає, що ми можемо довіряти результатам регресійної моделі та безпечно інтерпретувати коефіцієнти моделі.
Однак якщо залишковий графік оцінюється як «поганий», це означає, що результати моделі ненадійні, і нам потрібно підібрати іншу модель регресії до даних.
Наведені нижче приклади пояснюють, як інтерпретувати «хороші» та «погані» залишкові ділянки на практиці.
Приклад 1: «хороший» залишковий слід
Припустімо, що ми підбираємо регресійну модель і отримуємо наступний графік залишків:
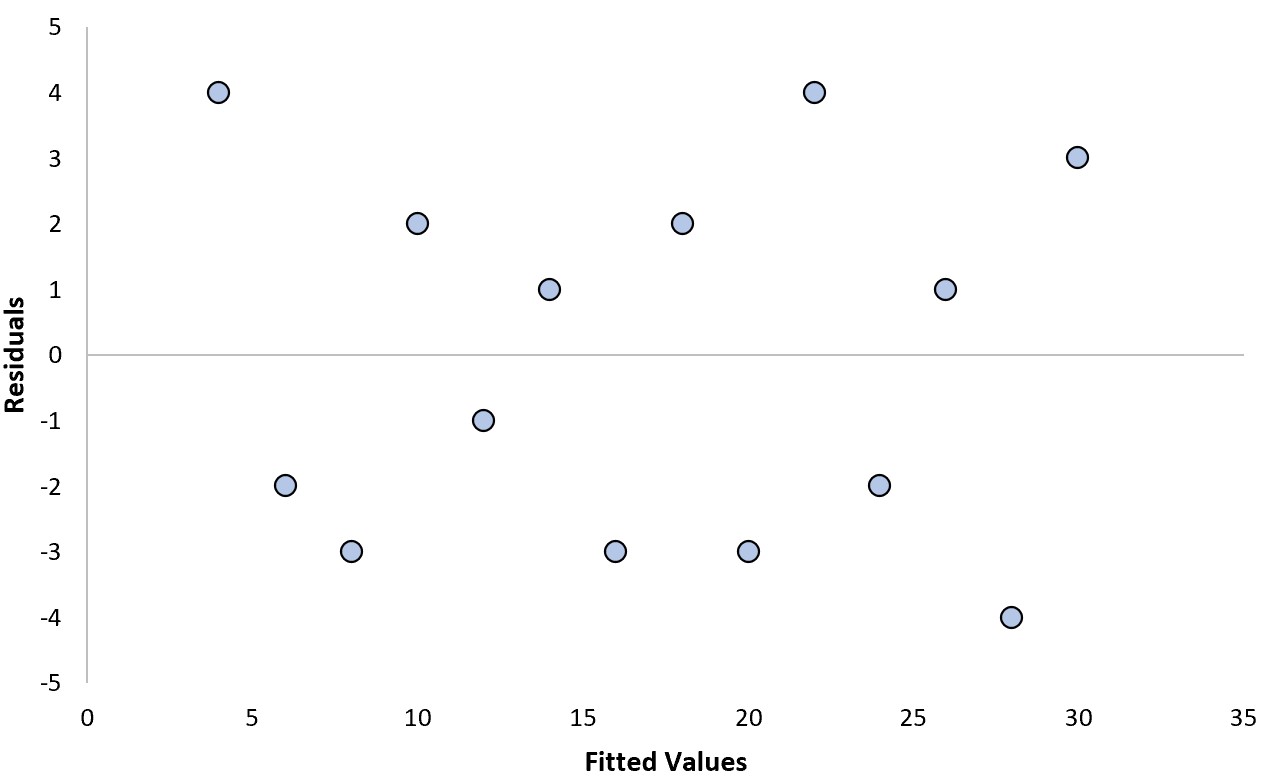
Ми можемо відповісти на наступні два запитання, щоб визначити, чи це «хороша» залишкова ділянка:
1. Чи демонструють залишки чітку тенденцію?
Ні. Залишки випадковим чином розкидані навколо нуля без чіткої моделі.
2. Залишки систематично збільшують або зменшують дисперсію?
Ні. Залишки мають досить постійну дисперсію (тобто відстань між залишками та нульовим значенням) на кожному рівні підігнаних значень.
Оскільки ми відповіли «Ні» на обидва ці запитання, ми б вважали це «хорошим» залишковим сюжетом.
Таким чином, ми можемо довіряти результатам регресійної моделі та безпечно інтерпретувати коефіцієнти моделі.
Приклад 2: «поганий» залишковий графік із чіткою моделлю
Припустімо, що ми підбираємо регресійну модель і отримуємо наступний графік залишків:
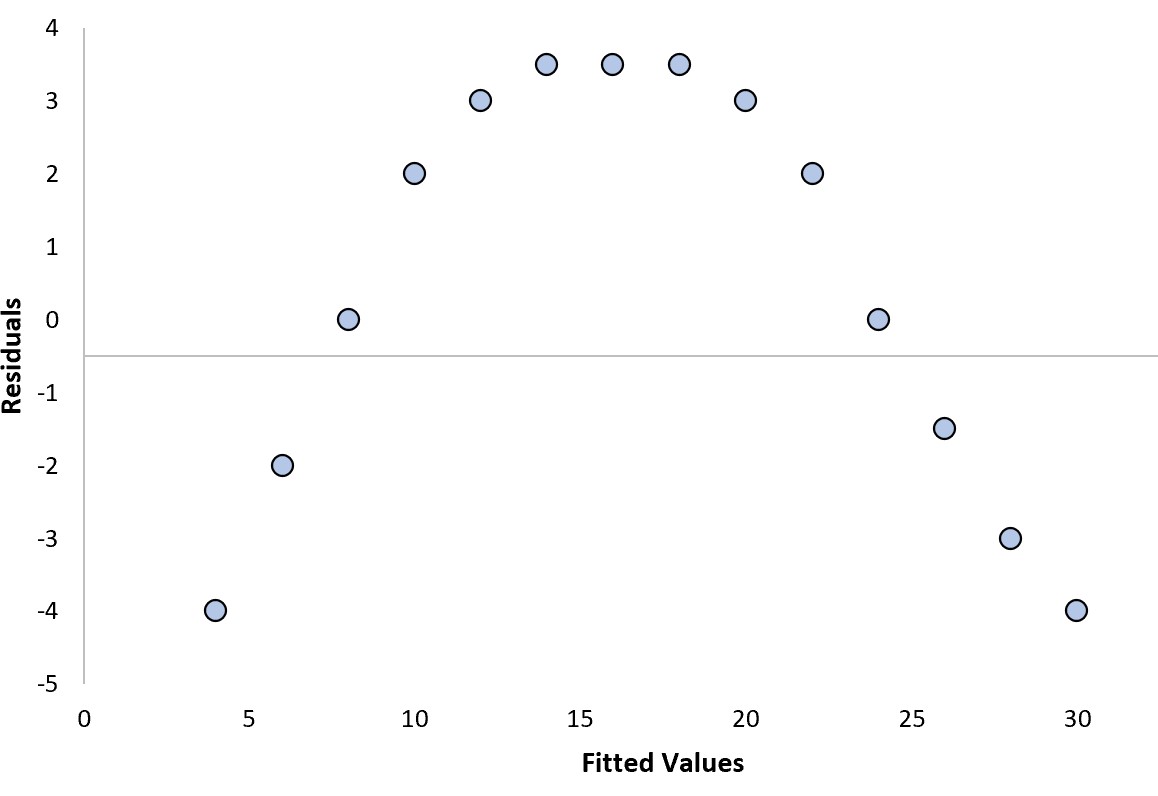
Ми можемо відповісти на наступні два запитання, щоб визначити, чи це «хороша» залишкова ділянка:
1. Чи демонструють залишки чітку тенденцію?
так Залишки мають вигнутий малюнок.
2. Залишки систематично збільшують або зменшують дисперсію?
так Залишки мають різні рівні дисперсії на різних рівнях підігнаних значень.
Оскільки ми відповіли «Так» принаймні на одне з цих запитань, ми вважаємо це «поганим» залишковим сюжетом.
Це означає, що регресійна модель не забезпечує належної відповідності даним.
Зокрема, викривлений візерунок на графіку залишків вказує на те, що модель лінійної регресії не відповідає даним і що модель квадратичної регресії, ймовірно, виконає краще завдання.
Приклад 3: «поганий» залишковий графік із зростаючою дисперсією
Припустімо, що ми підбираємо регресійну модель і отримуємо наступний графік залишків:
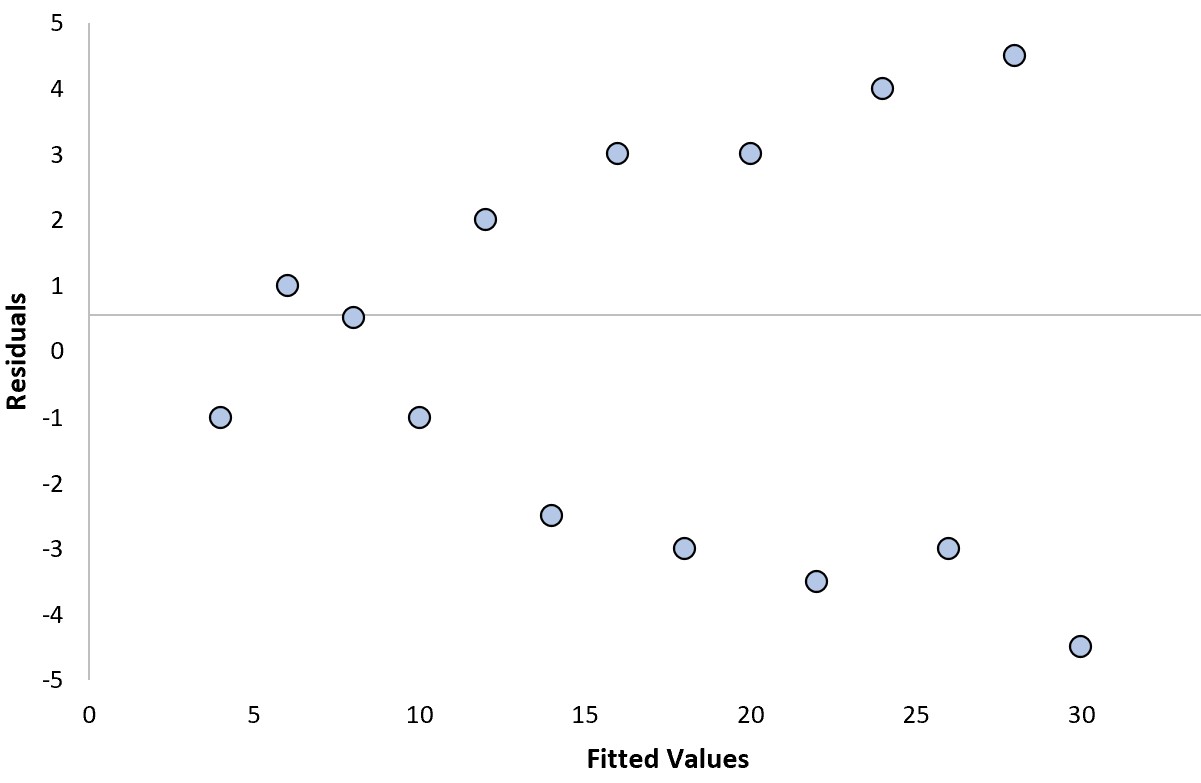
Ми можемо відповісти на наступні два запитання, щоб визначити, чи це «хороша» залишкова ділянка:
1. Чи демонструють залишки чітку тенденцію?
Ні. Немає чіткої тенденції щодо залишків.
2. Залишки систематично збільшують або зменшують дисперсію?
так Дисперсія залишків збільшується зі збільшенням підігнаних значень.
Оскільки ми відповіли «Так» принаймні на одне з цих запитань, ми вважаємо це «поганим» залишковим сюжетом.
У цьому конкретному прикладі залишки страждають від гетероскедастичності , яка стосується неоднакової дисперсії залишків на різних рівнях підігнаних значень.
Це означає, що результати регресійної моделі можуть бути ненадійними.
Зверніться до цієї статті , щоб дізнатися про різні способи вирішення проблеми гетероскедастичності в регресійній моделі.
Додаткові ресурси
У наступних посібниках пояснюється, як створити графіки залишків за допомогою різного статистичного програмного забезпечення:
Як створити ділянку залишків у R
Як створити залишковий графік у Python
Як створити діаграму залишку в Excel
Як створити ділянку залишку в SAS