Як виконати тест на відповідність хі-квадрату в excel

Тест відповідності хі-квадрат використовується для визначення того, чи відповідає категоріальна змінна гіпотетичному розподілу.

У цьому посібнику пояснюється, як виконати тест відповідності хі-квадрат у Excel.

Приклад: тест відповідності хі-квадрат у Excel

Власник магазину каже, що кожен день тижня до його магазину приходить однакова кількість покупців. Щоб перевірити цю гіпотезу, незалежний дослідник фіксує кількість покупців, які прийшли в магазин за певний тиждень, і знаходить наступне:

• Понеділок: 50 клієнтів
• Вівторок: 60 клієнтів
• Середа: 40 клієнтів
• Четвер: 47 клієнтів
• П’ятниця: 53 клієнтів

Ми використаємо наступні кроки, щоб виконати тест відповідності хі-квадрат, щоб визначити, чи дані відповідають заяві власника магазину.

Крок 1: Введіть дані.

Спочатку ми введемо значення даних для очікуваної кількості клієнтів щодня в одному стовпці та спостережуваної кількості клієнтів щодня в іншому стовпці:

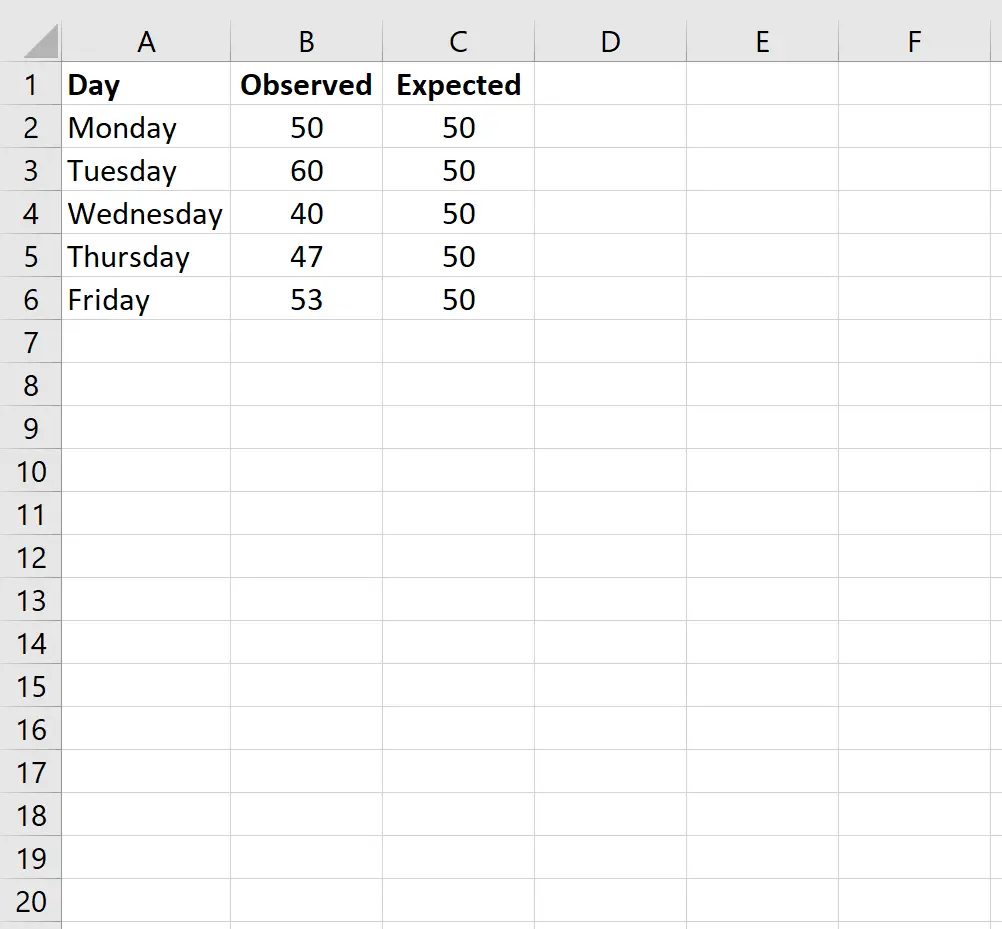
Примітка. Загалом було 250 клієнтів. Отже, якщо власник магазину очікує, що щодня до магазину входитиме однакова кількість покупців, він буде очікувати мати 50 покупців на день.

Крок 2: Знайти різницю між спостережуваними та очікуваними значеннями.

Статистичний показник хі-квадрат для тесту на відповідність становить X ² = Σ(OE) ² / E.

золото:

• Σ: химерний символ, що означає «сума»
• O: спостережуване значення
• E: очікуване значення

Наступна формула показує, як обчислити (OE) ² /E для кожного рядка:

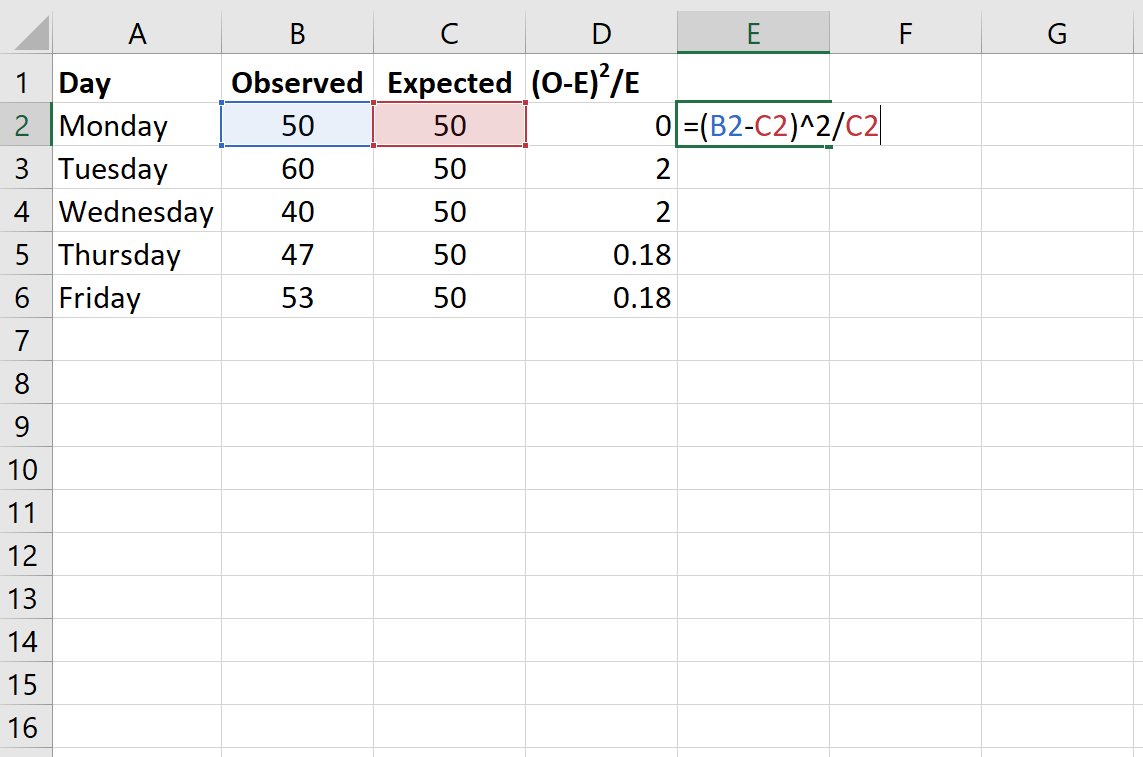
Крок 3. Обчисліть статистику хі-квадрат і відповідне значення p.

Нарешті, ми розрахуємо статистику хі-квадрат, а також відповідне значення p за такими формулами:

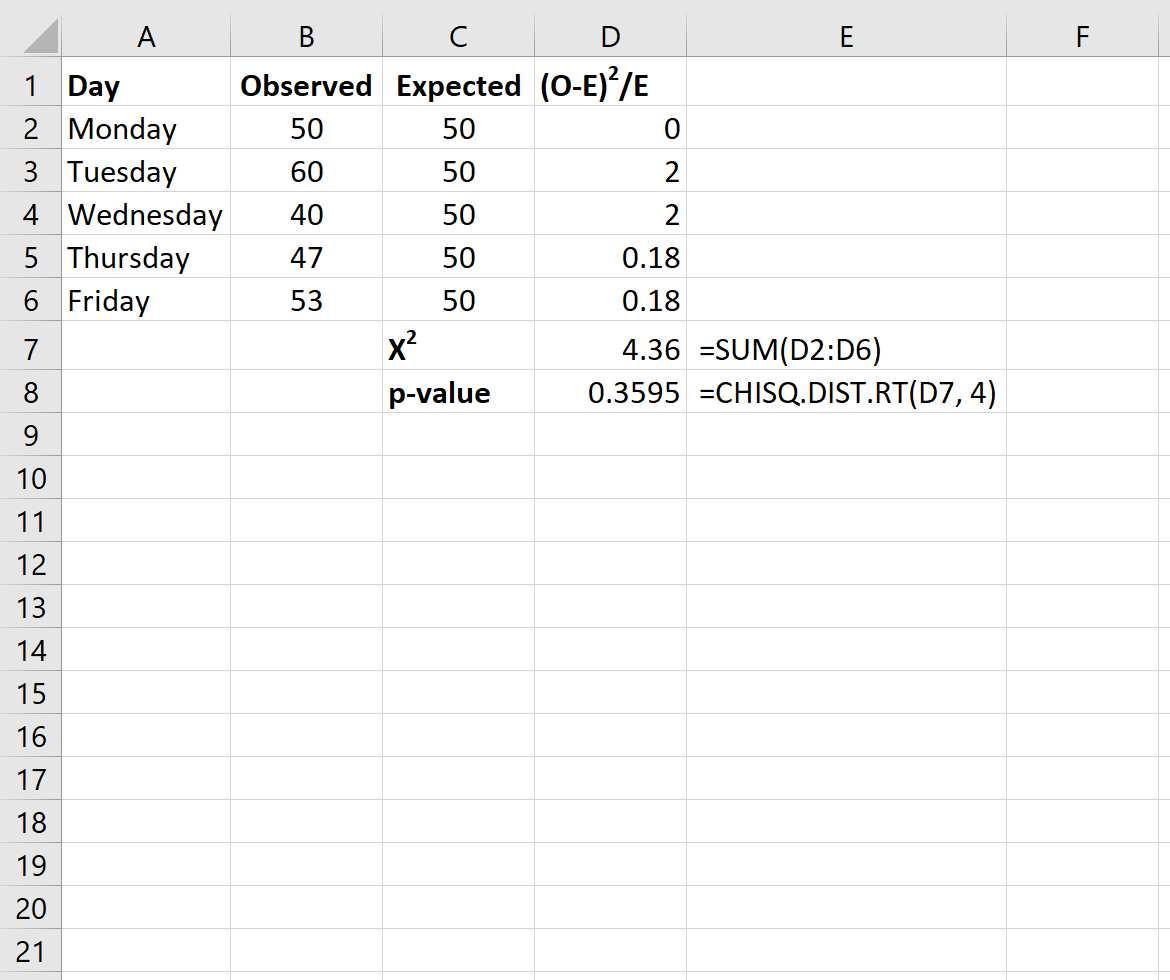
Примітка. Функція Excel CHISQ.DIST.RT(x, deg_freedom) повертає правильну ймовірність розподілу хі-квадрат, пов’язану з тестовою статистикою x і певним ступенем свободи. Ступені свободи обчислюються як n-1. У цьому випадку deg_freedom = 5 – 1 = 4.

Крок 4: Інтерпретація результатів.

Статистика тесту ^X2 для тесту становить 4,36 , а відповідне значення p — 0,3595 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що справжній розподіл клієнтів відрізняється від того, про який повідомляє власник магазину.