Центральна гранична теорема

У цій статті пояснюється, що таке центральна гранична теорема (CLT) і для чого вона використовується в статистиці. Ви також знайдете формулу центральної граничної теореми та приклад її застосування, розв’язаний крок за кроком.

Що таке центральна гранична теорема?

У статистиці центральна гранична теорема , також звана центральною граничною теоремою , стверджує, що розподіл вибіркових середніх наближається до нормального розподілу зі збільшенням розміру вибірки, незалежно від розподілу ймовірностей сукупності.

Тобто центральна гранична теорема говорить, що якщо ми беремо достатньо велику кількість вибірок, середнє значення цих вибірок можна наблизити до нормального розподілу.

Крім того, центральна гранична теорема стверджує, що вибіркове середнє наближатиметься до значення генеральної сукупності зі збільшенням розміру вибірки. Це дозволяє апроксимувати параметри статистичної сукупності. Нижче ми побачимо, як це робиться.

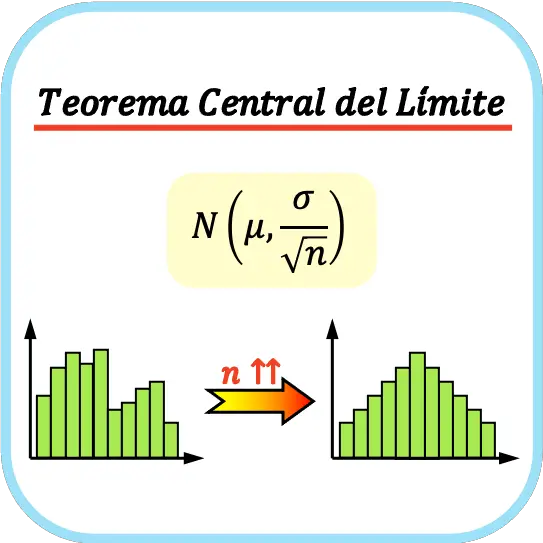
Загалом вважається, що для застосування центральної граничної теореми розмір вибірки має складати щонайменше 30 спостережень, хоча це залежить від характеристик досліджуваної змінної.

Центральна гранична теорема має багато застосувань, оскільки нормальний розподіл дозволяє робити висновки статистичних розрахунків, таких як перевірка гіпотез або довірчі інтервали. Наприклад, у фінансах центральна гранична теорема використовується для аналізу прибутку та ризику інвестицій.

Приклад центральної граничної теореми

Після того, як ми побачили визначення центральної граничної теореми, давайте розглянемо приклад, щоб повністю зрозуміти її значення.

Прикладом центральної граничної теореми є кидання кубика. Кидок кубика відбувається за дискретним рівномірним розподілом , оскільки всі результати є рівноімовірними. Але розподіл суми кількох результатів наближається до нормального розподілу.

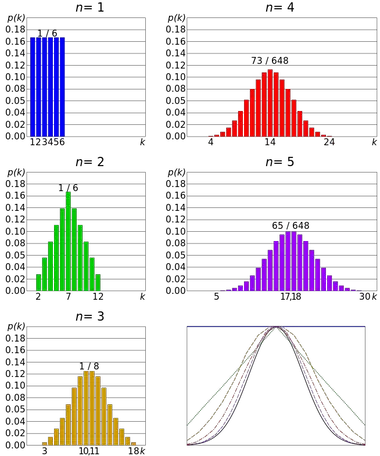
Таким чином, чим більше кидків, тим більша ймовірність того, що форма розподілу засобів буде нагадувати графік нормального розподілу.

Формула центральної граничної теореми

Центральна гранична теорема стверджує, що якщо генеральна сукупність має середнє значення μ і стандартне відхилення σ і ми беремо достатньо велику кількість вибірок (n≥30), набір середніх вибіркових значень можна наблизити до нормального розподілу із середнім значенням μ і стандартним відхиленням σ /√n.

Крім того , _якщо X _{1 ,} до нормального розподілу, визначеного такою формулою:

Розв’язана вправа центральної граничної теореми

Щоб ви могли повністю засвоїти концепцію, ось розв’язана вправа центральної граничної теореми.

• Компанія продає деталі, які використовуються для заміни певних компонентів іграшки. Монета має середню вагу 300 г і стандартне відхилення 50 г. Якщо клієнт замовив партію з 100 штук, яка ймовірність того, що середня вага шматків у партії буде більшою за 305 г? А яка ймовірність того, що партія зі 100 штук важить більше 31 кг?

Оскільки розмір партії великий (n=100), ми можемо застосувати центральну граничну теорему для вирішення проблеми.

Таким чином, використовуючи формулу центральної граничної теореми, розподіл вибіркових середніх можна апроксимувати до нормального розподілу з такими параметрами:

Тепер ми виконуємо процес введення, щоб потім знайти ймовірність, яку вимагає вправа. Для цього нам потрібно від розподілу відняти середнє значення, а потім розділити на стандартне відхилення:

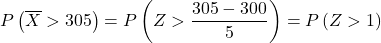таблиці нормального розподілу :

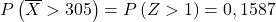
Отже, ми повторюємо процес введення, а потім знаходимо другу ймовірність, яку запитує проблема:

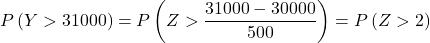
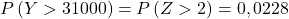➤ Див.: Закон великих чисел