Як застосувати центральну граничну теорему в r (з прикладами)

Центральна гранична теорема стверджує, що вибірковий розподіл вибіркового середнього є приблизно нормальним, якщо розмір вибірки достатньо великий, навіть якщо розподіл сукупності не є нормальним.

Центральна гранична теорема також стверджує, що вибірковий розподіл матиме такі властивості:

1. Середнє значення розподілу вибірки дорівнюватиме середньому значенню розподілу сукупності:

x = µ

2. Стандартне відхилення розподілу вибірки дорівнюватиме стандартному відхиленню розподілу сукупності, поділеному на розмір вибірки:

s = σ /n

У наступному прикладі показано, як застосувати центральну граничну теорему в R.

Приклад: застосування центральної граничної теореми в R

Припустимо, що ширина панцира черепахи рівномірно розподілена з мінімальною шириною 2 дюйми та максимальною шириною 6 дюймів.

Тобто, якщо ми навмання виберемо черепаху та виміряємо ширину її панцира, вона також, імовірно, буде від 2 до 6 дюймів завширшки .

Наступний код показує, як створити набір даних у R, що містить вимірювання ширини панцира 1000 черепах, рівномірно розподілених між 2 і 6 дюймами:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

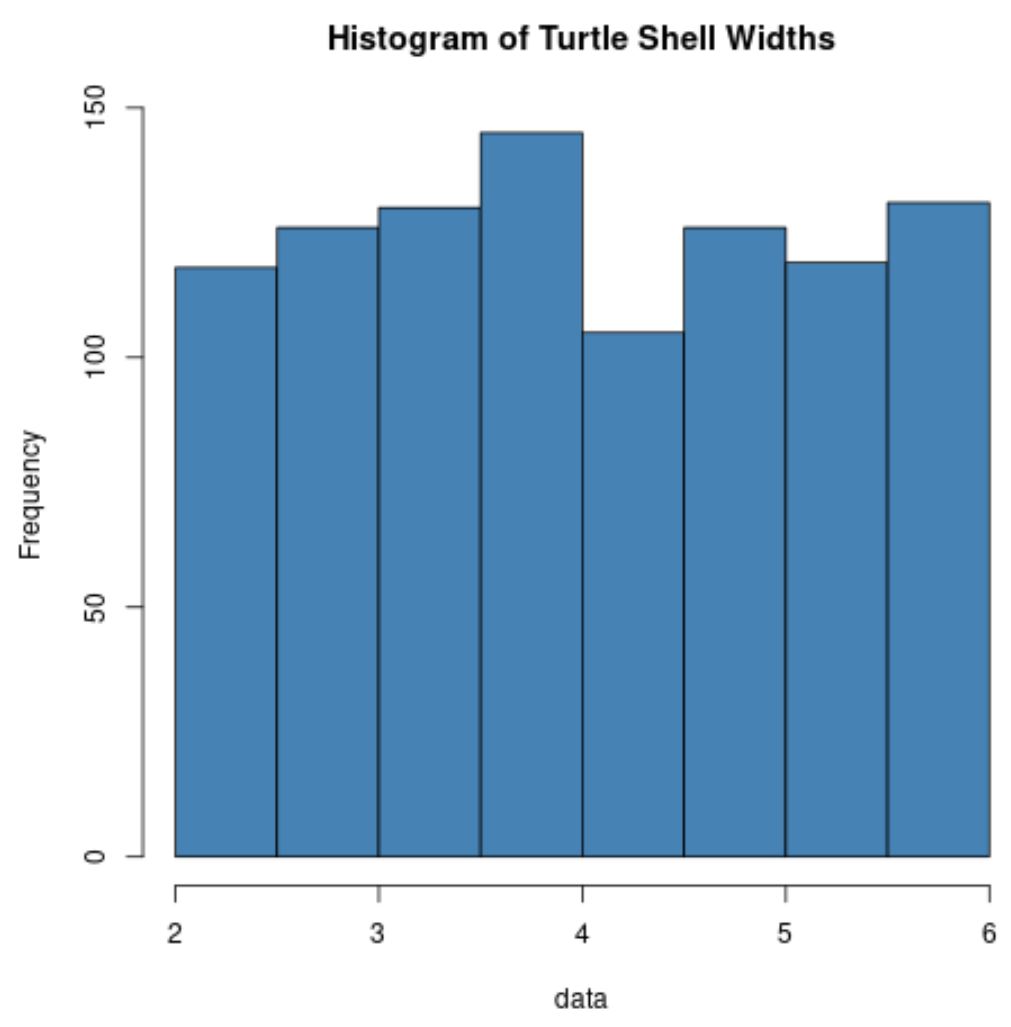
Зверніть увагу, що розподіл ширини панцира черепахи зазвичай не розподілений взагалі.

А тепер уявіть, що ми беремо повторні випадкові зразки 5 черепах із цієї популяції та вимірюємо середнє значення вибірки знову і знову.

Наступний код показує, як виконати цей процес у R і створити гістограму для візуалізації розподілу вибіркових середніх:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

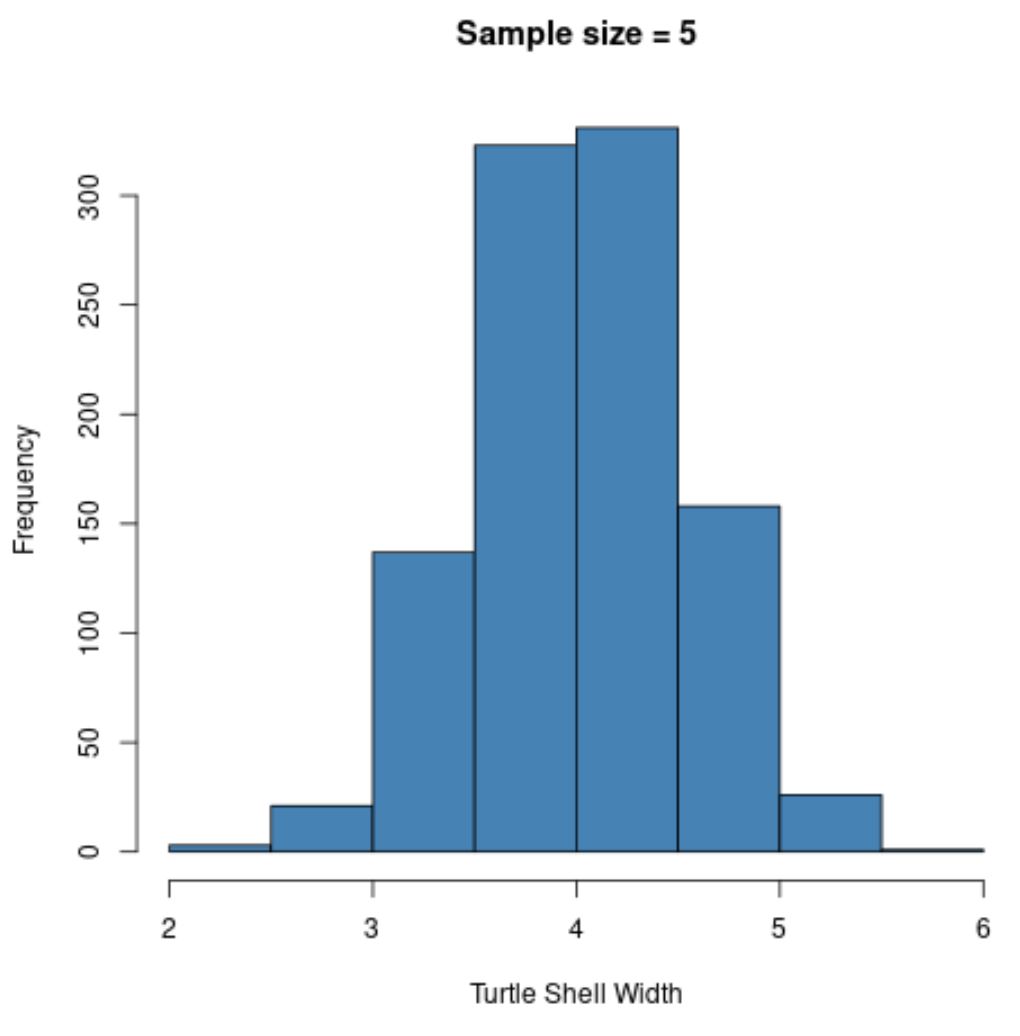
Зауважте, що вибірковий розподіл вибіркових середніх виглядає нормально розподіленим, навіть якщо розподіл, з якого походять вибірки, не був нормально розподіленим.

Також зверніть увагу на середнє значення вибірки та стандартне відхилення вибірки для цього розподілу вибірки:

• x̄ : 4,008
• s : 0,517

Тепер припустімо, що ми збільшимо розмір вибірки, яку використовуємо, з n=5 до n=30 і відтворимо гістограму вибіркових середніх:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

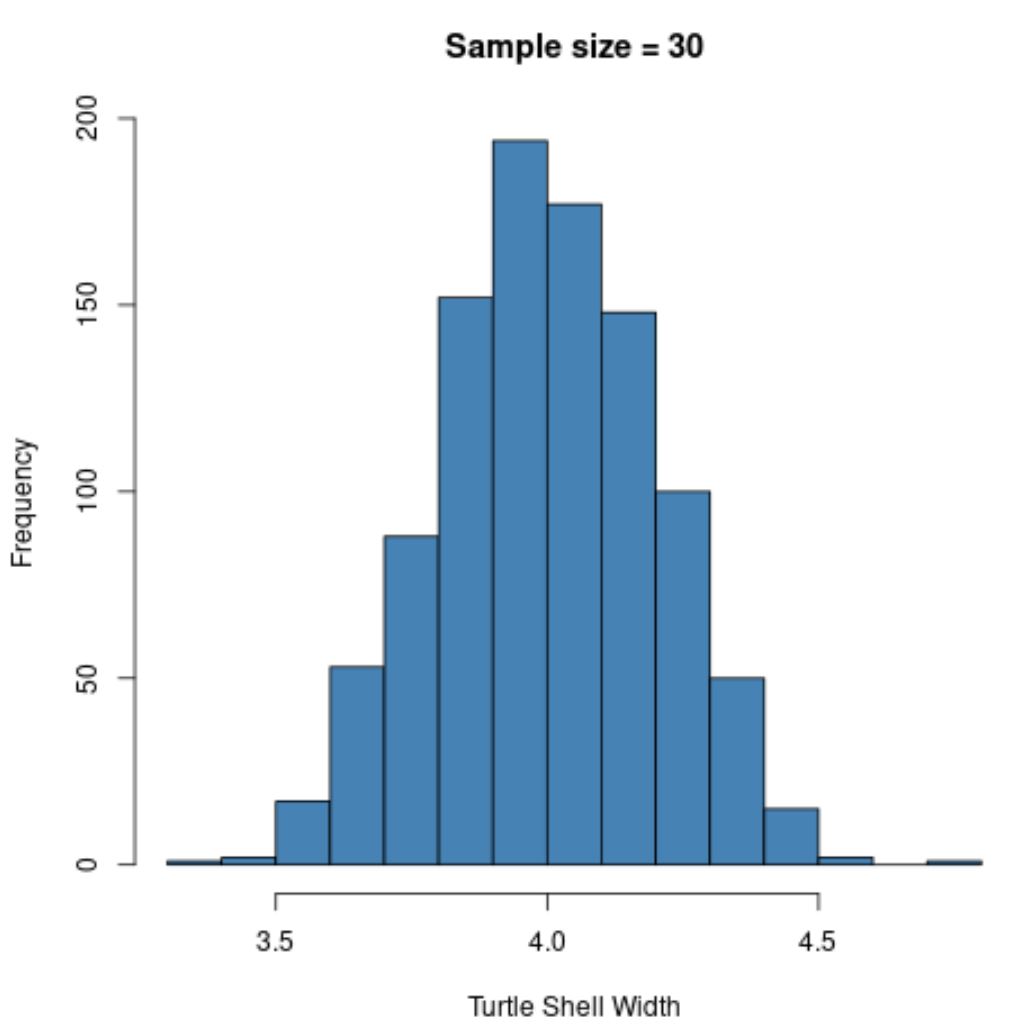
Вибірковий розподіл знову має нормальний розподіл , але стандартне відхилення вибірки ще менше:

• s : 0,200

Це пояснюється тим, що ми використовували більший розмір вибірки (n=30) порівняно з попереднім прикладом (n=5), тому стандартне відхилення вибіркових середніх є ще меншим.

Якщо ми продовжуємо використовувати все більші і більші вибірки, ми виявимо, що стандартне відхилення вибірки стає все меншим і меншим.

Це ілюструє центральну граничну теорему на практиці.

Додаткові ресурси

Наступні ресурси надають додаткову інформацію про центральну граничну теорему:

Вступ до центральної граничної теореми
Калькулятор центральної граничної теореми
5 прикладів використання центральної граничної теореми в реальному житті