Часткові найменші квадрати в r (крок за кроком)

Одна з найпоширеніших проблем, з якою ви зіткнетеся під час машинного навчання, — мультиколінеарність . Це відбувається, коли дві або більше змінних предиктора в наборі даних сильно корельовані.

Коли це трапляється, модель може добре відповідати навчальному набору даних, але може працювати погано на новому наборі даних, який вона ніколи не бачила, оскільки він переповнює навчальний набір даних. навчальний набір.

Один із способів вирішити цю проблему — використати метод часткових найменших квадратів , який працює наступним чином:

• Стандартизуйте змінні предиктора та відповіді.
• Обчисліть M лінійних комбінацій (званих «компонентами PLS») p початкових змінних предикторів, які пояснюють значну кількість варіацій як у змінній відповіді, так і в змінних предикторів.
• Використовуйте метод найменших квадратів, щоб підібрати модель лінійної регресії, використовуючи компоненти PLS як предиктори.
• Використовуйте k-кратну перехресну перевірку , щоб знайти оптимальну кількість компонентів PLS для збереження в моделі.

Цей підручник надає покроковий приклад того, як виконувати часткові найменші квадрати в R.

Крок 1: Завантажте необхідні пакети

Найпростіший спосіб виконати частковий метод найменших квадратів у R – це використовувати функції в пакеті pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Крок 2. Підберіть часткову модель найменших квадратів

Для цього прикладу ми використаємо вбудований набір даних R під назвою mtcars , який містить дані про різні типи автомобілів:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Для цього прикладу ми підберемо модель часткових найменших квадратів (PLS), використовуючи hp як змінну відповіді та наступні змінні як змінні прогнозу:

• миль на галлон
• дисплей
• лайно
• вага
• qsec

Наступний код показує, як підігнати модель PLS до цих даних. Зверніть увагу на такі аргументи:

• scale=TRUE : це повідомляє R, що кожна зі змінних у наборі даних повинна бути масштабована, щоб мати середнє значення 0 і стандартне відхилення 1. Це гарантує, що жодна змінна предиктора не має надто сильного впливу на модель, якщо вимірюється в різних одиницях.
• validation=”CV” : Це повідомляє R використовувати k-кратну перехресну перевірку для оцінки продуктивності моделі. Зауважте, що за умовчанням використовується k=10 згорток. Також зауважте, що замість цього можна вказати «LOOCV», щоб виконати перехресну перевірку Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Крок 3: Виберіть кількість компонентів PLS

Після встановлення моделі нам потрібно визначити, скільки компонентів PLS залишити.

Для цього просто подивіться на тестову середню квадратичну помилку (тест RMSE), розраховану за допомогою k-cross перевірки:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

У результаті вийшли дві цікаві таблиці:

1. ПЕРЕВІРКА: RMSEP

У цій таблиці наведено тест RMSE, розрахований шляхом k-кратної перехресної перевірки. Ми бачимо наступне:

• Якщо ми використовуємо лише вихідний термін у моделі, RMSE тесту становить 69,66 .
• Якщо ми додамо перший компонент PLS, тест RMSE падає до 40,57.
• Якщо ми додамо другий компонент PLS, тест RMSE падає до 35,48.

Ми бачимо, що додавання додаткових компонентів PLS фактично призводить до збільшення RMSE тесту. Таким чином, здається, що оптимальним було б використовувати лише два компоненти PLS у кінцевій моделі.

2. НАВЧАННЯ: пояснення % відхилення

Ця таблиця повідомляє нам про відсоток дисперсії у змінній відповіді, що пояснюється компонентами PLS. Ми бачимо наступне:

• Використовуючи лише перший компонент PLS, ми можемо пояснити 68,66% варіації змінної відповіді.
• Додавши другий компонент PLS, ми можемо пояснити 89,27% варіації змінної відповіді.

Зауважте, що ми все одно зможемо пояснити більшу дисперсію, використовуючи більше компонентів PLS, але ми бачимо, що додавання більше ніж двох компонентів PLS фактично не значно збільшує відсоток поясненої дисперсії.

Ми також можемо візуалізувати тест RMSE (поряд із тестом MSE і R-квадрат) як функцію кількості компонентів PLS за допомогою функції validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

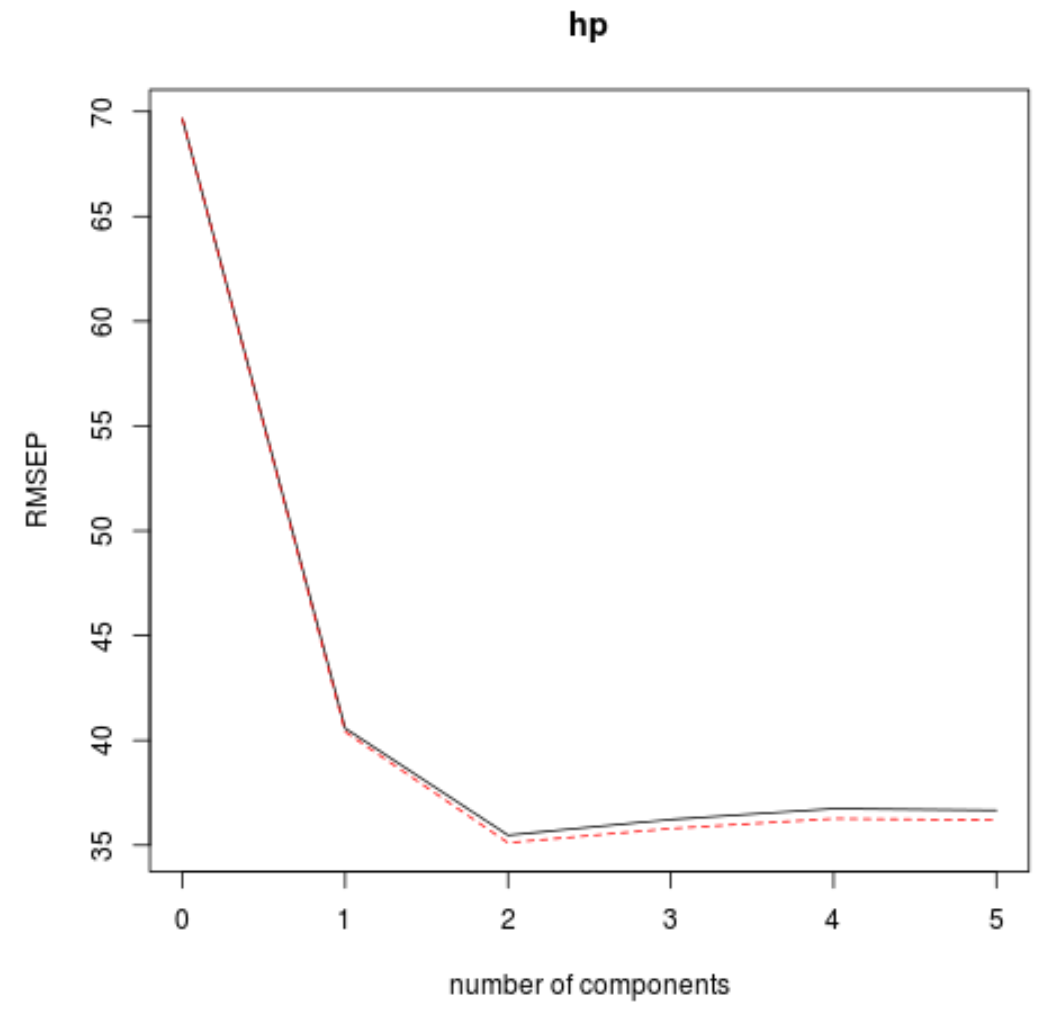
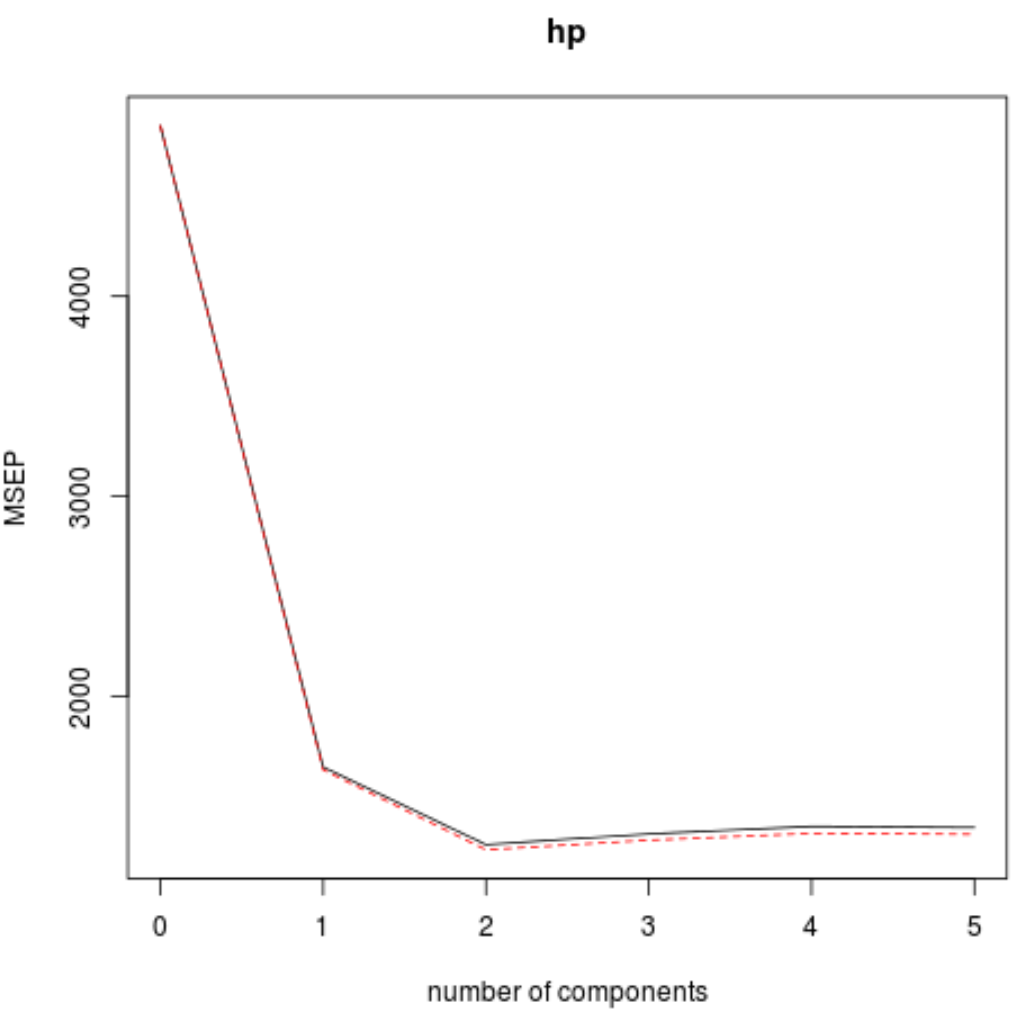
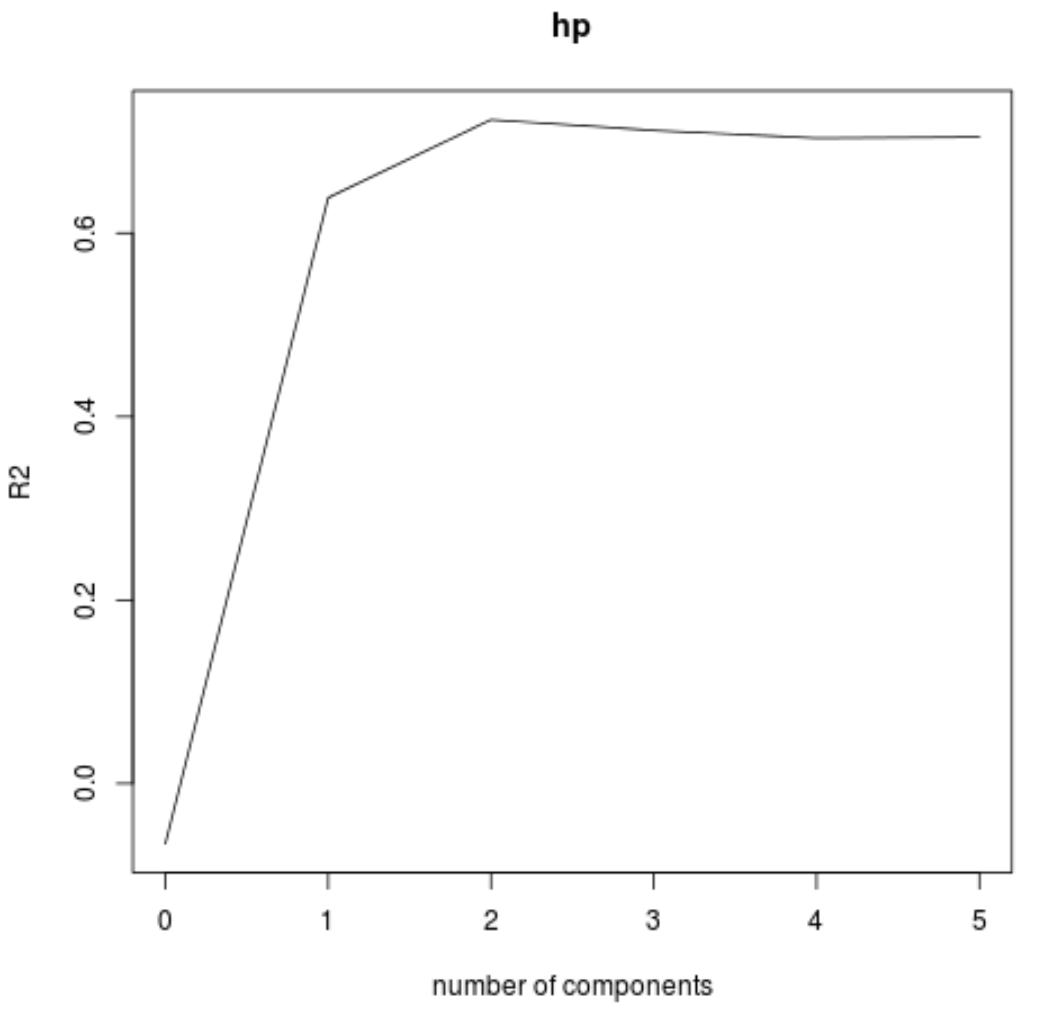
На кожному графіку ми бачимо, що підгонка моделі покращується шляхом додавання двох компонентів PLS, але має тенденцію погіршуватися, коли ми додаємо більше компонентів PLS.

Таким чином, оптимальна модель включає лише перші два компоненти PLS.

Крок 4. Використовуйте остаточну модель для прогнозування

Ми можемо використовувати остаточну модель із двома компонентами PLS, щоб робити прогнози щодо нових спостережень.

У наведеному нижче коді показано, як розділити вихідний набір даних на навчальний і тестовий набір і використовувати остаточну модель із двома компонентами PLS для прогнозування на тестовому наборі.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Ми бачимо, що RMSE тесту виявляється 54,89609 . Це середнє відхилення між прогнозованим значенням hp і спостережуваним значенням hp для спостережень тестового набору.

Зауважте, що еквівалентна регресійна модель головних компонентів із двома головними компонентами дала тестове RMSE 56,86549 . Таким чином, модель PLS трохи перевершила модель PCR для цього набору даних.

Повне використання коду R у цьому прикладі можна знайти тут .