Що вважається «слабким»; кореляція?
У статистиці ми часто прагнемо зрозуміти, як дві змінні співвідносяться одна з одною. Наприклад, ми можемо захотіти знати:
- Який зв’язок між кількістю годин навчання студента та оцінкою, яку він отримує на іспиті?
- Який зв’язок між зовнішньою температурою та кількістю батончиків морозива, які продає фуд-трак?
- Який зв’язок між доларами, витраченими на рекламу, та загальним доходом, отриманим для даного бізнесу?
У кожному сценарії ми хочемо зрозуміти зв’язок між двома змінними.
Одним із найпоширеніших способів кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який є мірою лінійного зв’язку між двома змінними.
Він завжди приймає значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Це число, яке часто позначається як r , допомагає нам зрозуміти силу зв’язку між двома змінними. Чим ближче r до нуля, тим слабший зв’язок між двома змінними .
Важливо відзначити, що дві змінні можуть мати слабку позитивну або слабку негативну кореляцію.
Слабка позитивна кореляція: коли одна змінна зростає, інша змінна також має тенденцію до зростання, але лише слабко або ненадійно.
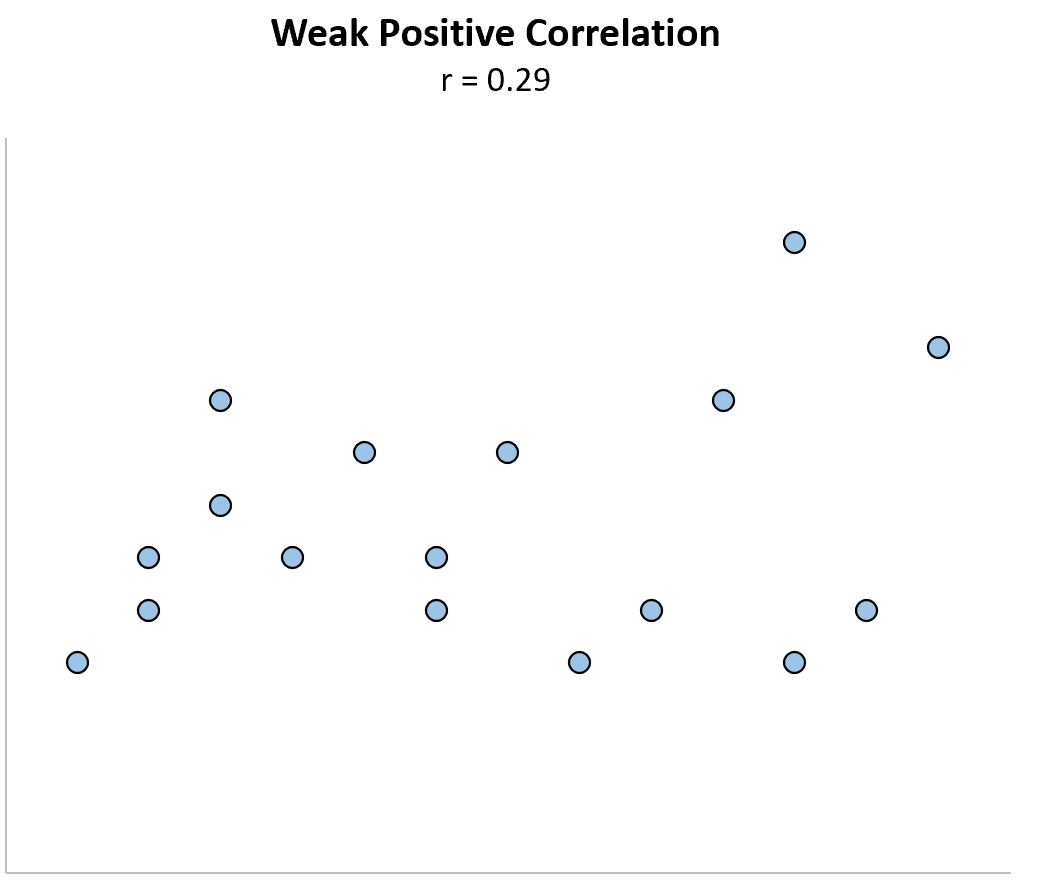
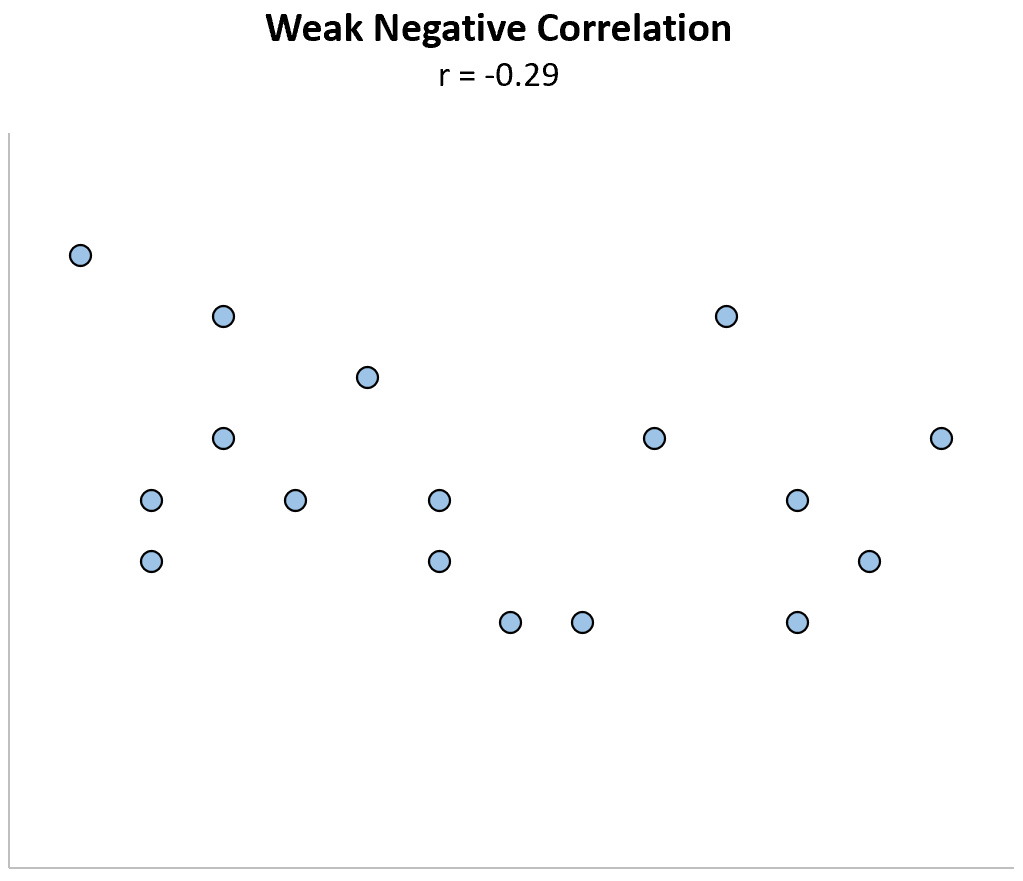
Низька негативна кореляція: коли одна змінна збільшується, інша змінна має тенденцію до зменшення, але лише слабко або ненадійно.
У наведеній нижче таблиці показано емпіричне правило для інтерпретації сили зв’язку між двома змінними на основі значення r :
| Абсолютне значення r | Міцність відносин |
|---|---|
| r < 0,25 | Жодних стосунків |
| 0,25 < r < 0,5 | Слабкі стосунки |
| 0,5 < r < 0,75 | Помірні стосунки |
| r > 0,75 | Міцні стосунки |
Кореляція між двома змінними вважається низькою, якщо абсолютне значення r знаходиться в межах від 0,25 до 0,5.
Однак визначення «слабкої» кореляції може відрізнятися від поля до поля.
Медичний
У медицині визначення «слабкого» зв’язку часто набагато нижче. Якщо зв’язок між прийомом певного препарату та зниженням частоти серцевих нападів становить r = 0,2, це може вважатися «відсутністю зв’язку» в інших галузях, але в медицині це досить суттєво, що варто приймати ліки, щоб зменшити ризик серцевих нападів. . мати серцевий напад.
Людські ресурси
У такій сфері, як людські ресурси, нижчі кореляції також використовуються частіше. Наприклад, було показано, що кореляція між середнім балом у коледжі та продуктивністю роботи становить приблизно r = 0,16 . Це досить мало, але досить важливо, щоб компанія принаймні врахувала це під час співбесіди.
технології
У технологічних сферах кореляція між змінними може бути набагато вищою, щоб вважатися «низькою». Наприклад, якщо компанія створює безпілотний автомобіль і кореляція між рішеннями автомобіля щодо повороту та ймовірністю уникнення аварії становить r = 0,95 , це можна вважати «слабкою» кореляцією та, ймовірно, занадто слабкою для автомобіля вважати безпечним, тому що неправильне рішення може бути фатальним.
Використовуйте діаграми розсіювання для візуалізації кореляцій
Під час розрахунку коефіцієнта кореляції між двома змінними корисно створити діаграму розсіювання, щоб також візуалізувати кореляцію.
Зокрема, хмари точок мають дві переваги:
1. Діаграма розсіювання може допомогти вам визначити викиди, які впливають на коефіцієнт кореляції.
Екстремальний викид може мати великий вплив на коефіцієнт кореляції. Розглянемо наведений нижче приклад, у якому змінні X і Y мають коефіцієнт кореляції Пірсона r = 0,91 .
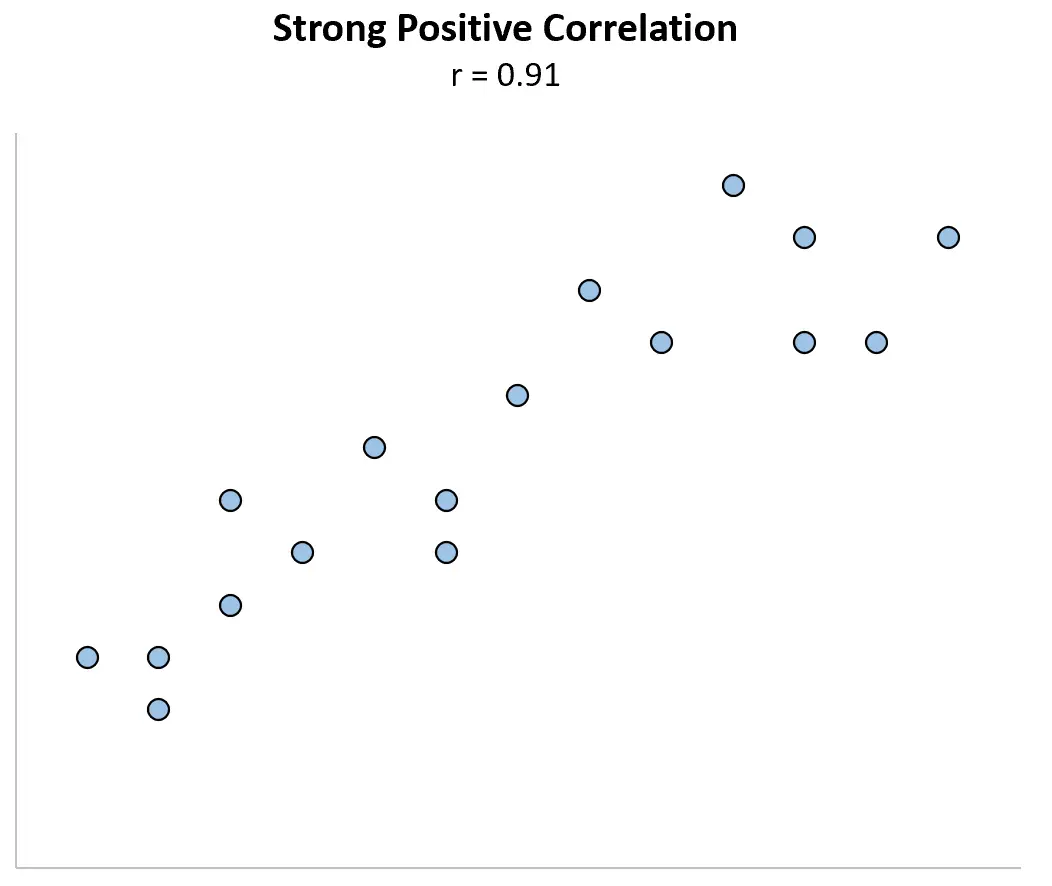
Тепер уявіть, що ми змінюємо першу точку даних на набагато більшу. Коефіцієнт кореляції раптово стає r = 0,29 .
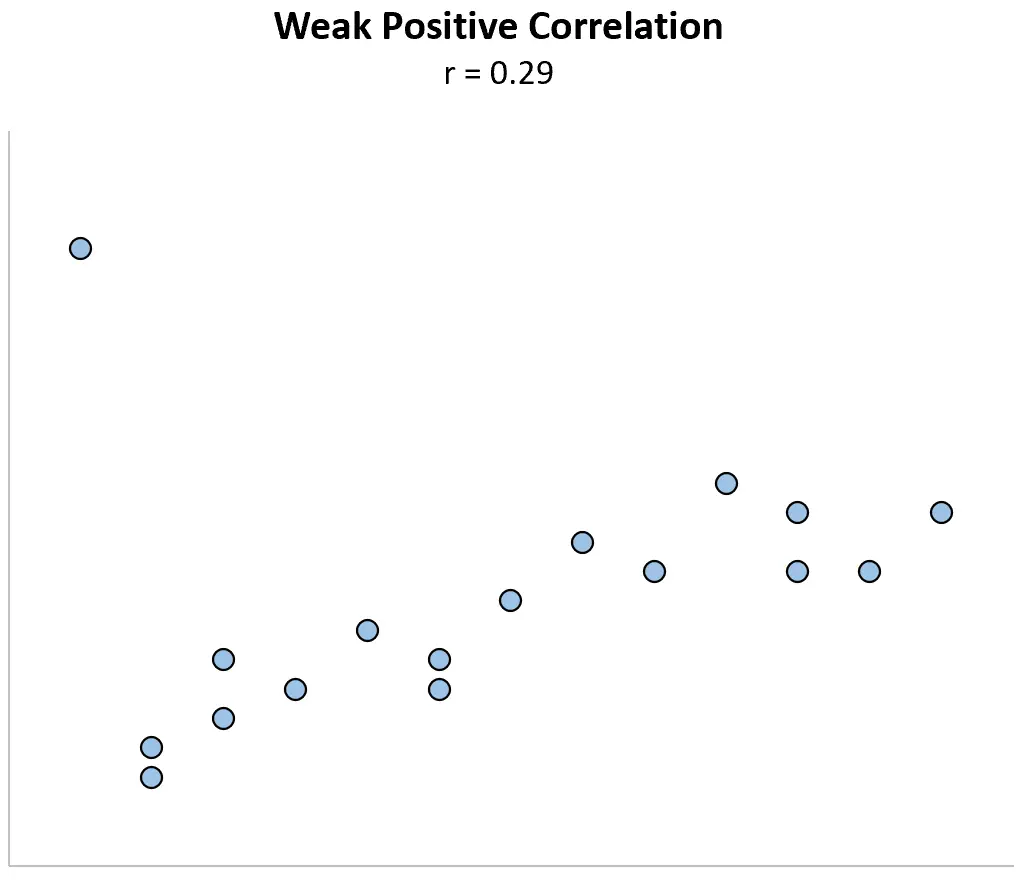
Ця єдина точка даних змінює коефіцієнт кореляції з сильно позитивного зв’язку на слабко позитивний.
(2) Діаграма розсіювання може допомогти вам визначити нелінійні зв’язки між змінними.
Коефіцієнт кореляції Пірсона просто повідомляє нам, чи є дві змінні лінійно пов’язаними. Але навіть якщо коефіцієнт кореляції Пірсона говорить нам, що дві змінні не корельовані, вони все одно можуть мати якийсь нелінійний зв’язок.
Наприклад, розглянемо наведену нижче діаграму розсіювання між змінними X і Y , у якій їх кореляція r = 0,00 .
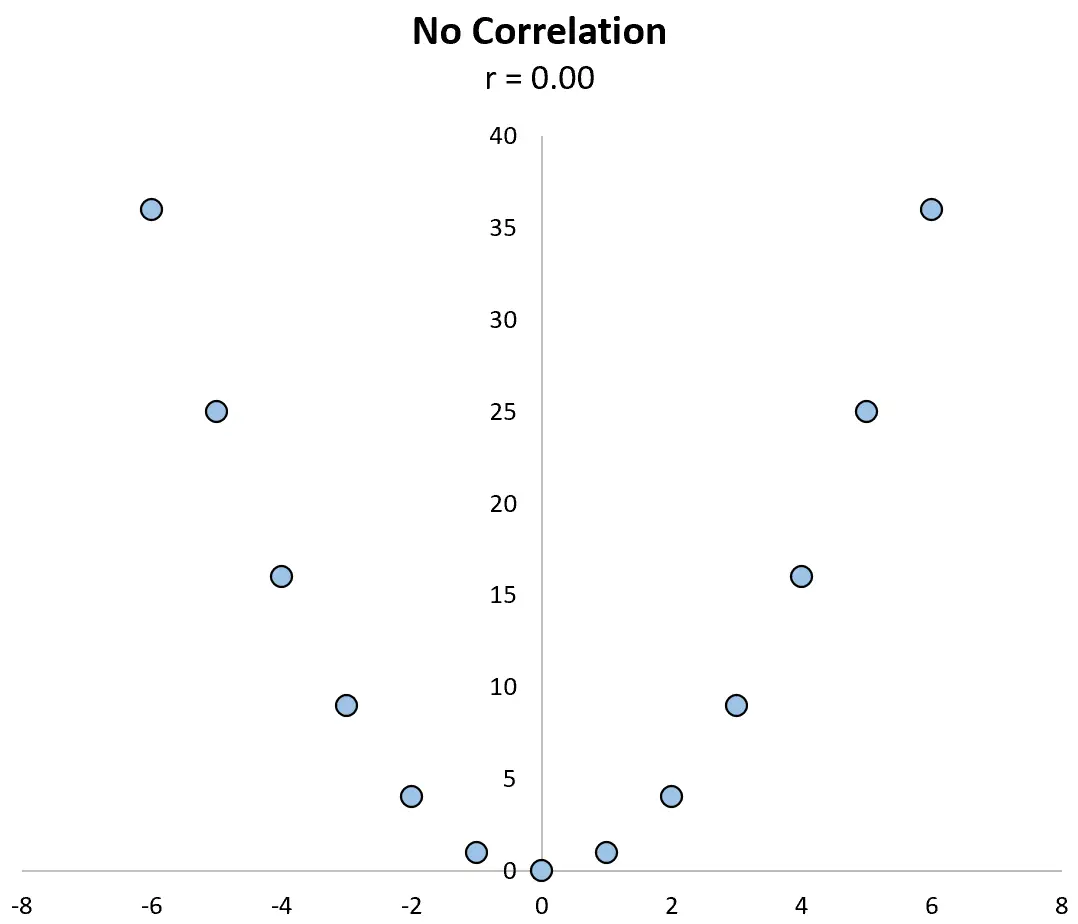
Очевидно, що змінні не мають лінійного зв’язку, але вони мають нелінійний зв’язок: значення y – це просто значення x у квадраті.
Коефіцієнт кореляції сам по собі не може виявити цю залежність, але діаграма розсіювання може.
Висновок
Підсумовуючи:
1. Як правило, коефіцієнт кореляції між 0,25 і 0,5 вважається «слабкою» кореляцією між двома змінними.
2. Це емпіричне правило може відрізнятися залежно від регіону. Наприклад, набагато нижчу кореляцію можна вважати слабкою в медичній галузі порівняно з технологічною. Обов’язково використовуйте свій досвід у темі, щоб вирішити, що вважати низькою кореляцією.
3. При використанні коефіцієнта кореляції для опису зв’язку між двома змінними також корисно створити діаграму розсіювання, щоб ви могли ідентифікувати викиди в наборі даних, а також потенційний нелінійний зв’язок.
Додаткові ресурси
Що вважається «сильною» кореляцією?
Калькулятор кореляційної матриці
Кореляція vs. асоціація: яка різниця?