Що це означає, якщо статистика стійка?

Статистику називають стійкою , якщо вона не чутлива до екстремальних значень.

Ось два приклади стійкої статистики:

• Медіана
• Міжквартильний діапазон

Ось приклади статистичних даних, які не витримують :

• Середня
• Стандартне відхилення
• охайний

Наступний приклад ілюструє різницю між стійкою та нестійкою статистикою.

Приклад: стійка та нестійка статистика

Припустимо, що ми маємо наступний набір даних:

Набір даних: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Використовуючи калькулятор або статистичне програмне забезпечення, ми можемо обчислити значення наступних статистичних даних для цього набору даних:

• Медіана: 13
• Інтерквартильний діапазон: 13,5

Ми також можемо обчислити значення наступної нестійкої статистики для цього набору даних:

• Середній: 13,54
• Стандартне відхилення: 8,82
• Діапазон: 27

Тепер подумайте, чи додано до цього набору даних екстремальний викид:

Набір даних: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Ми знову можемо обчислити значення наступної стійкої статистики для цього набору даних:

• Медіана: 14
• Міжквартильний діапазон: 15,75

Ми також можемо обчислити значення наступної нестійкої статистики для цього набору даних:

• Середній: 49,92
• Стандартне відхилення: 126,27
• Діапазон: 448

Зверніть увагу, наскільки змінилася статистика відсутності опору, просто додавши екстремальне значення до набору даних:

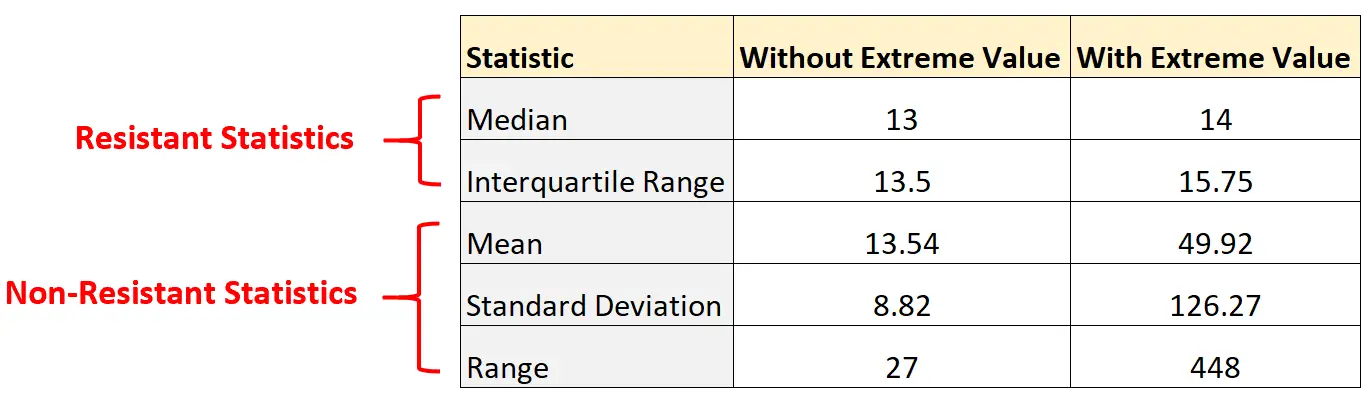
І навпаки, статистика опору майже не змінилася. Медіана та інтерквартильний діапазон змінилися лише незначно.

Коли використовувати стійку статистику

Найбільш часто використовуваними статистичними даними для вимірювання центру та дисперсії значень у наборі даних є середнє значення та стандартне відхилення відповідно.

На жаль, обидві ці статистики чутливі до екстремальних значень. Отже, якщо в наборі даних присутні викиди, середнє значення та стандартне відхилення не будуть точно описувати розподіл значень у наборі даних.

Замість цього рекомендується використовувати медіану та інтерквартильний діапазон для вимірювання центру та дисперсії значень у наборі даних, якщо присутні викиди, оскільки обидві ці статистики надійні .

Додаткові ресурси

Як викиди впливають на середнє значення?
Коли використовувати середнє значення проти медіани
Коли використовувати інтерквартильний діапазон проти стандартного відхилення