Як вручну обчислити значення p з тесту t

Одним із найбільш часто використовуваних тестів у статистиці є t-критерій , який часто використовують для визначення того, чи дорівнює середнє значення сукупності певному значенню.

Наприклад, скажімо, ми хочемо знати, чи дорівнює середня висота певного виду рослин 15 дюймам. Щоб перевірити це, ми могли б зібрати випадкову вибірку з 20 рослин, знайти середнє значення вибірки та стандартне відхилення вибірки та виконати t-тест, щоб визначити, чи справді середня висота становить 15 дюймів.

Нульова та альтернативна гіпотези тесту такі:

H ₀ : µ = 15

H _a : µ ≠ 15

Формула тестової статистики така:

t = ( X -μ) / (s/ √n )

де x — вибіркове середнє, μ — гіпотетичне середнє (у нашому прикладі воно буде 15), s — стандартне відхилення вибірки, а n — розмір вибірки.

Коли ми знаємо значення t , ми можемо використовувати статистичне програмне забезпечення або онлайн-калькулятор, щоб знайти відповідне значення p. Якщо p-значення нижче певного альфа-рівня (звичайні варіанти 0,01, 0,05 і 0,10), ми можемо відхилити нульову гіпотезу та зробити висновок, що середня висота рослини не дорівнює 15 дюймам.

Однак також можна вручну оцінити тестове значення p за допомогою таблиці t-розподілу . У цій статті ми пояснимо, як це зробити.

Приклад: обчислення p-значення вручну за t-тестом

Проблема : Боб хоче знати, чи дорівнює середня висота певного виду рослин 15 дюймам. Щоб перевірити це, він збирає випадкову вибірку з 20 рослин і виявляє, що середня вибірка становить 14 дюймів, а стандартне відхилення вибірки становить 3 дюйми. Виконайте t-тест, використовуючи альфа-рівень 0,05, щоб визначити, чи справжній середній зріст населення насправді становить 15 дюймів.

рішення:

Крок 1: Сформулюйте нульову та альтернативну гіпотези.

H ₀ : µ = 15

H _a : µ ≠ 15

Крок 2: Знайдіть статистику тесту.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Крок 3: Знайдіть p-значення для тестової статистики.

Щоб знайти p-значення вручну, нам потрібно використовувати таблицю t-розподілу з n-1 ступенями свободи. У нашому прикладі розмір нашої вибірки становить n = 20, тому n-1 = 19.

У наведеній нижче таблиці t-розподілу нам потрібно подивитися на рядок, який відповідає «19» зліва, і спробувати знайти абсолютне значення нашої тестової статистики 1,49 .

Зверніть увагу, що 1,49 не відображається в таблиці, але воно знаходиться між двома значеннями 1,328 і 1,729 .

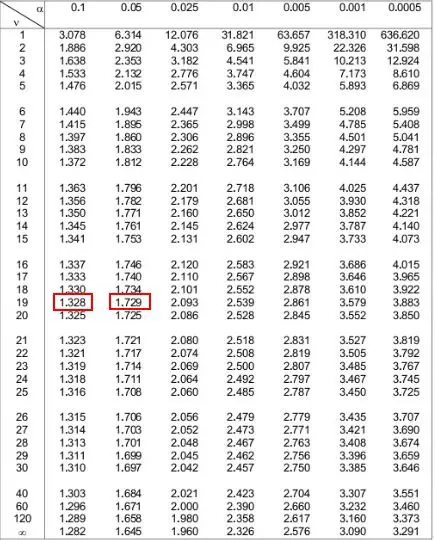
Потім ми можемо подивитися на два альфа-рівні у верхній частині таблиці, які відповідають цим двом числам. Ми бачимо, що вони дорівнюють 0,1 і 0,05 .

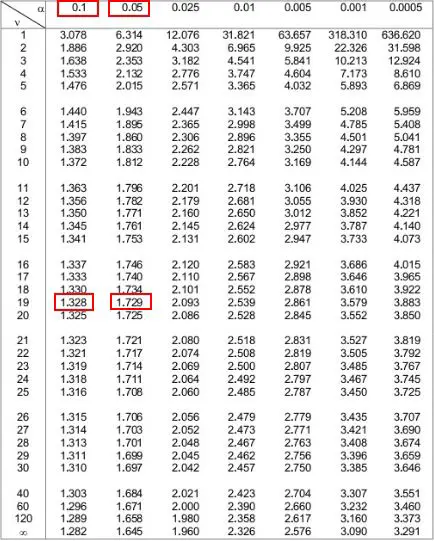
Це означає, що p-значення для одностороннього тесту становить від 0,1 до 0,05. Назвемо це .075. Оскільки наш t-критерій є двостороннім, нам потрібно помножити це значення на 2. Отже, наше оцінене p-значення дорівнює 0,075 * 2 = 0,15 .

Крок 4: Зробіть висновок.

Оскільки це значення p не нижче обраного альфа-рівня 0,05, ми не можемо відхилити нульову гіпотезу. Таким чином, ми не маємо достатньо доказів, щоб стверджувати, що справжня середня висота цього виду рослини є чимось іншим, ніж 15 дюймів.

Перевірте результати за допомогою калькулятора

Ми можемо підключити нашу статистику t -критерію та ступені свободи до онлайн-калькулятора p-значення, щоб побачити, наскільки наше оцінене значення p було близьким до справжнього значення p:

Справжнє p-значення становить 0,15264 , що досить близько до нашого розрахункового p-значення 0,15 .

Висновок

У цій статті ми побачили, що можна вручну оцінити p-значення t-тесту за допомогою таблиці t-розподілу. Однак у більшості випадків вам ніколи не доведеться обчислювати значення p вручну, і ви можете використовувати або статистичне програмне забезпечення, як-от R і Excel, або онлайн-калькулятор, щоб знайти точне значення p для тесту.

У більшості випадків, особливо в ретельних статистичних дослідженнях і експериментах, ви захочете скористатися калькулятором, щоб знайти точне p-значення за t-тестом, щоб бути якомога точним, але корисно знати, що ви завжди можете вручну оцінити p-значення з t-критерію, якщо вам це абсолютно необхідно.