Як читати коваріаційну матрицю

Коваріація — це міра того, як зміни в одній змінній пов’язані зі змінами в другій змінній. Точніше, це міра ступеня лінійного зв’язку двох змінних.

Коваріаційна матриця – це квадратна матриця, яка показує коваріацію між багатьма різними змінними. Це може бути корисним способом зрозуміти, як різні змінні пов’язані в наборі даних.

У наступному прикладі показано, як читати коваріаційну матрицю на практиці.

Як читати коваріаційну матрицю

Припустімо, що ми маємо наступну коваріаційну матрицю, яка містить інформацію про результати іспитів з трьох різних предметів для студентів:

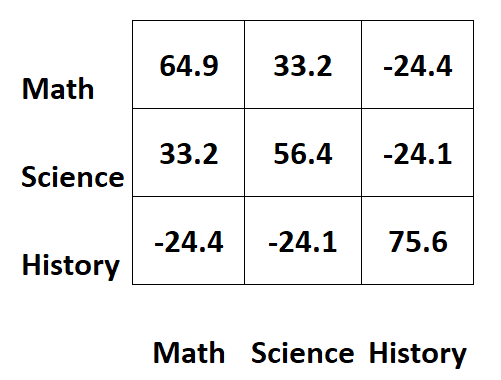
Значення вздовж діагоналей матриці представляють дисперсії кожного предмета.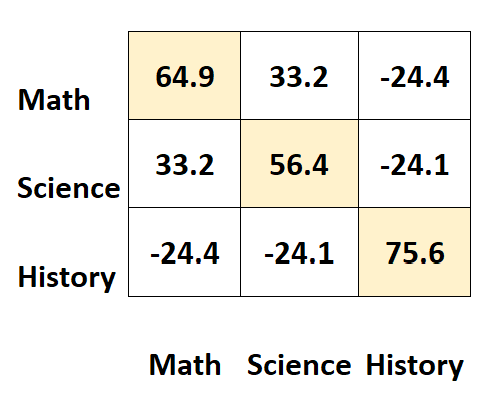

Наприклад:

• Дисперсія результатів з математики становить 64,9 .
• Дисперсія наукових балів становить 56,4 .
• Дисперсія історичних балів становить 75,6 .

Інші значення матриці представляють коваріації між різними предметами.

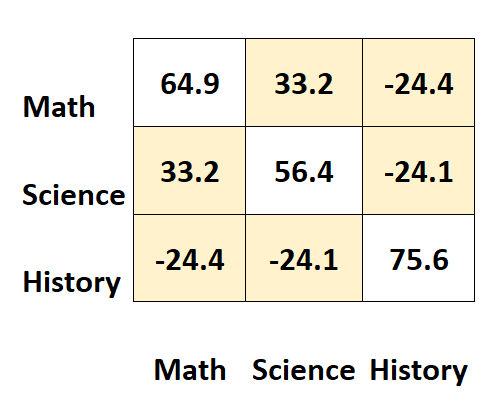
Наприклад:

• Коваріація між балами з математики та природничих наук становить 33,2 .
• Коваріація між оцінками з математики та історії становить –24,4 .
• Коваріація між балами з науки та історії становить –24,1 .

Додатне число для коваріації вказує на те, що дві змінні мають тенденцію до збільшення або зменшення в тандемі.

Наприклад, математика та природничі науки мають позитивну коваріацію ( 33.2 ), що вказує на те, що учні, які мають високі результати з математики, також, як правило, отримують високі результати з природничих наук.

Навпаки, учні, які мають погані результати в математиці, також, як правило, мають погані результати в науках.

Від’ємне число для коваріації вказує на те, що коли одна змінна збільшується, друга змінна має тенденцію до зменшення.

Наприклад, математика та історія мають негативну коваріацію ( -24,44 ), що вказує на те, що учні з високими показниками з математики, як правило, мають низькі показники з історії.

Навпаки, учні, які мають низькі результати з математики, зазвичай отримують високі результати з історії.

Примітка про симетрію коваріаційної матриці

Слід зазначити, що коваріаційна матриця абсолютно симетрична.

Наприклад, у верхній правій клітинці відображається точно таке ж значення, як у нижній лівій клітинці:

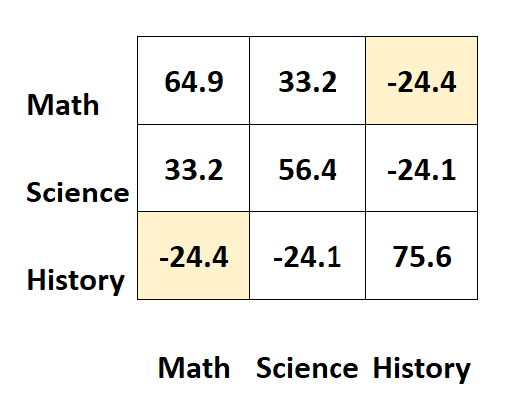
Дійсно, дві комірки вимірюють коваріацію між історією та математикою.

Оскільки коваріаційна матриця є симетричною, половина значень коваріації, які відображаються в матриці, є зайвими та непотрібними.

Таким чином, іноді буде показано лише половину коваріаційної матриці:

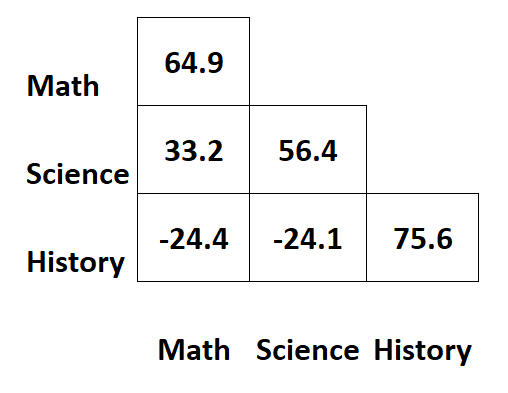
Коли використовувати коваріаційну матрицю

На практиці вам часто доведеться створювати та інтерпретувати кореляційну матрицю частіше, ніж коваріаційну матрицю.

Однак коваріаційні матриці часто використовуються «під капотом» для різних алгоритмів і моделей машинного навчання.

Наприклад, коваріаційна матриця використовується під час аналізу головних компонентів , що допомагає нам зрозуміти основні закономірності в наборі даних, що містить велику кількість змінних.

Додаткові ресурси

У наступних посібниках пояснюється, як створити коваріаційну матрицю за допомогою різного статистичного програмного забезпечення:

Як створити коваріаційну матрицю в R
Як створити коваріаційну матрицю в Python
Як створити коваріаційну матрицю в SPSS
Як створити коваріаційну матрицю в Excel