Як читати кореляційну матрицю

У статистиці ми часто прагнемо зрозуміти зв’язок між двома змінними.

Наприклад, ми можемо захотіти зрозуміти зв’язок між кількістю годин навчання студента та оцінкою, яку він отримує на іспиті.

Одним із способів кількісного визначення цього зв’язку є використання коефіцієнта кореляції Пірсона , який є мірою лінійного зв’язку між двома змінними . Він має значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Чим далі коефіцієнт кореляції від нуля, тим сильніший зв’язок між двома змінними.

За темою: що вважається «сильною» кореляцією?

Але в деяких випадках ми хочемо зрозуміти кореляцію між кількома парами змінних. У цих випадках ми можемо створити кореляційну матрицю , яка є квадратною таблицею, яка показує коефіцієнти кореляції між декількома змінними.

Приклад кореляційної матриці

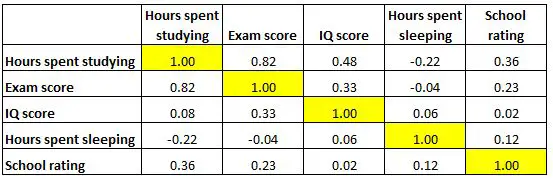
Наведена нижче кореляційна матриця представляє коефіцієнти кореляції між декількома змінними, пов’язаними з освітою:

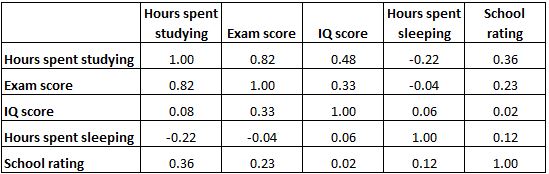
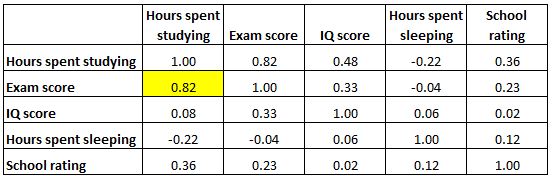
Кожна клітинка таблиці показує кореляцію між двома конкретними змінними. Наприклад, у виділеній клітинці нижче показано, що кореляція між «годинами, витраченими на навчання» та «оцінкою іспиту» становить 0,82 , що вказує на те, що вони сильно корелюють. Більше годин, витрачених на навчання, тісно пов’язане з вищими оцінками на іспитах.

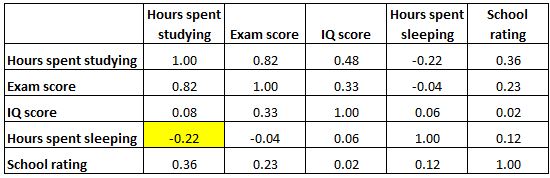
А виділена клітинка нижче показує, що кореляція між «годинами, витраченими на навчання» та «годинами, витраченими на сон», становить -0,22 , що вказує на слабку негативну кореляцію між ними. Більше годин, проведених на навчання, пов’язано з меншою кількістю годин, проведених на сон.

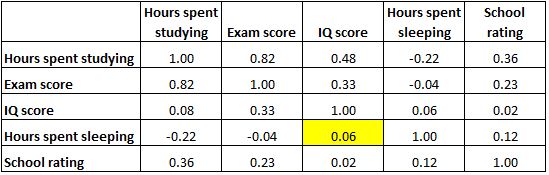
А виділена клітинка нижче показує, що кореляція між «годинами, проведеними уві сні» та «оцінкою IQ» становить 0,06 , що вказує на те, що вони в основному не корельовані. Існує дуже мало зв’язку між кількістю годин сну студента та його показником IQ.

Також зауважте, що всі коефіцієнти кореляції вздовж діагоналі таблиці дорівнюють 1, оскільки кожна змінна ідеально корелює сама із собою. Ці клітини непридатні для інтерпретації.

Варіації кореляційної матриці

Зверніть увагу, що кореляційна матриця абсолютно симетрична. Наприклад, у верхній правій клітинці відображається точно таке ж значення, як у нижній лівій клітинці:

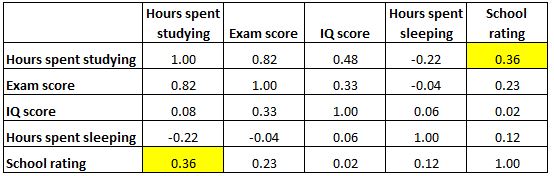
Дійсно, дві комірки вимірюють кореляцію між «годинами, витраченими на навчання» та «шкільною оцінкою».

Оскільки кореляційна матриця є симетричною, половина коефіцієнтів кореляції, які відображаються в матриці, є зайвими та непотрібними. Таким чином, іноді буде показано лише половину кореляційної матриці:

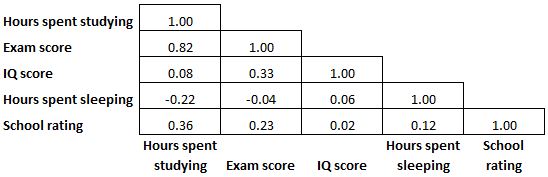
І іноді кореляційна матриця буде пофарбована як теплова карта, щоб зробити коефіцієнти кореляції ще легшими для читання:

Коли використовувати кореляційну матрицю

На практиці кореляційна матриця зазвичай використовується з трьох причин:

1. Кореляційна матриця зручно узагальнює набір даних.

Кореляційна матриця — це простий спосіб узагальнити кореляції між усіма змінними в наборі даних. Наприклад, припустімо, що у нас є такий набір даних, що містить таку інформацію про 1000 студентів:

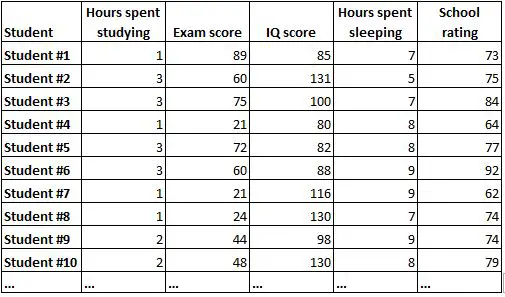
Було б дуже важко зрозуміти взаємозв’язок між кожною змінною, просто дивлячись на вихідні дані. На щастя, кореляційна матриця може допомогти нам швидко зрозуміти кореляції між кожною парою змінних.

2. Кореляційна матриця служить діагнозом для регресії.

Одним із ключових припущень множинної лінійної регресії є те, що жодна незалежна змінна в моделі не сильно корелює з будь-якою іншою змінною в моделі.

Коли дві незалежні змінні сильно корельовані, це призводить до проблеми, яка називається мультиколінеарністю , і може ускладнити інтерпретацію результатів регресії.

Один із найпростіших способів виявити потенційну проблему мультиколінеарності — подивитися на кореляційну матрицю та візуально перевірити, чи якась зі змінних сильно корелює одна з одною.

3. Кореляційну матрицю можна використовувати як вхідні дані для інших аналізів.

Кореляційна матриця використовується як вхідна інформація для інших комплексних аналізів, таких як пошуковий факторний аналіз і моделі структурних рівнянь.

Додаткові ресурси

У наступних посібниках пояснюється, як створити кореляційну матрицю за допомогою різноманітного статистичного програмного забезпечення:

Як створити кореляційну матрицю в Excel
Як створити кореляційну матрицю в SPSS
Як створити кореляційну матрицю в Stata
Як створити кореляційну матрицю в Python