Як читати таблицю розподілу хі-квадрат

Цей посібник пояснює, як читати та інтерпретувати діаграму розподілу хі-квадрат.

Що таке таблиця розподілу хі-квадрат?

Таблиця розподілу хі-квадрат – це таблиця, яка показує критичні значення розподілу хі-квадрат. Щоб використовувати таблицю розподілу хі-квадрат, вам потрібно знати лише два значення:

• Ступені свободи для тесту Хі-квадрат
• Альфа-рівень тесту (загальні варіанти: 0,01, 0,05 і 0,10)

На наступному зображенні показано перші 20 рядків таблиці розподілу хі-квадрат із ступенями свободи в лівій частині таблиці та альфа-рівнями у верхній частині таблиці:

Примітка. Повну таблицю розподілу хі-квадрат із більшою кількістю ступенів свободи можна знайти тут.

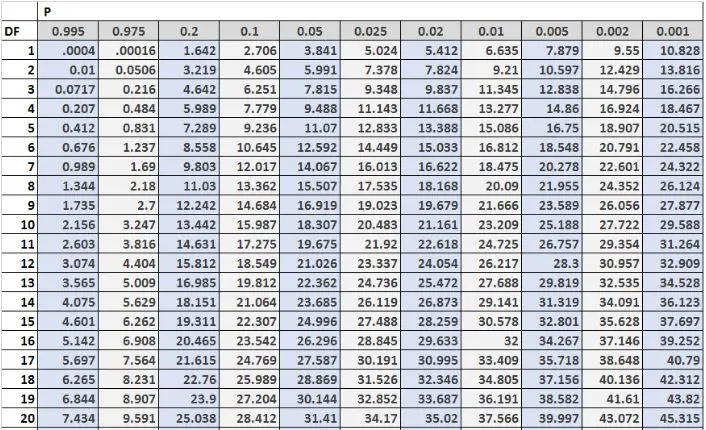
Критичні значення в таблиці часто порівнюють зі статистикою тесту хі-квадрат. Якщо статистика тесту перевищує критичне значення в таблиці, ви можете відхилити нульову гіпотезу тесту хі-квадрат і зробити висновок, що результати тесту є статистично значущими.

Приклади використання таблиці розподілу хі-квадрат

Ми покажемо, як використовувати таблицю розподілу хі-квадрат із такими трьома типами критеріїв хі-квадрат:

• Тест хі-квадрат на незалежність
• Тест хі-квадрат на відповідність
• Критерій хі-квадрат на однорідність

Тест хі-квадрат на незалежність

Ми використовуємо тест хі-квадрат для визначення незалежності , коли хочемо перевірити, чи існує значний зв’язок між двома категоріальними змінними.

Приклад: припустімо, ми хочемо знати, чи пов’язана стать із перевагами політичної партії. Ми беремо просту випадкову вибірку з 500 виборців і запитуємо їх про їхні переваги щодо політичної партії. Використовуючи рівень значущості 0,05, ми проводимо тест хі-квадрат, щоб визначити, чи стать пов’язана з перевагами політичних партій. У наступній таблиці представлені результати опитування:

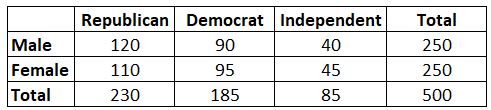
Виявляється, статистика тесту для цього тесту хі-квадрат становить 0,864.

Тоді ми можемо знайти критичне тестове значення в таблиці розподілу хі-квадрат. Ступені свободи дорівнюють (#рядки-1) * (#стовпці-1) = (2-1) * (3-1) = 2, і проблема сказала нам, що ми повинні використовувати альфа-рівень 0,05 Отже, згідно з таблицею розподілу хі-квадрат, критичне значення критерію становить 5,991 .

Оскільки наша тестова статистика менша за наше критичне значення, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що існує зв’язок між статтю та уподобаннями політичних партій.

Тест хі-квадрат на відповідність

Ми використовуємо тест відповідності хі-квадрат, коли хочемо перевірити, чи відповідає категоріальна змінна гіпотетичному розподілу.

Приклад: власник магазину каже, що 30% усіх його клієнтів у вихідні дні приходять у п’ятницю, 50% у суботу та 20% у неділю. Незалежний дослідник відвідує магазин у випадковий вихідний день і знаходить 91 покупця в п’ятницю, 104 у суботу та 65 у неділю. Використовуючи рівень значущості 0,10, ми виконуємо тест хі-квадрат, щоб перевірити відповідність даних і визначити, чи дані відповідають твердженням власника магазину.

У цьому випадку тестова статистика виявляється 10616.

Тоді ми можемо знайти критичне тестове значення в таблиці розподілу хі-квадрат. Ступені свободи дорівнюють (#outcomes-1) = 3-1 = 2, а проблема говорить нам, що ми повинні використовувати альфа-рівень 0,10. Отже, відповідно до таблиці розподілу хі-квадрат, критичне значення критерію становить 4,605 .

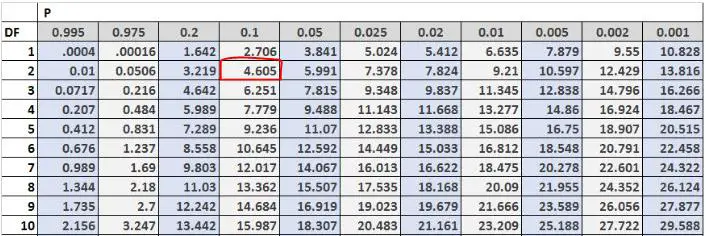
Оскільки наша тестова статистика перевищує наше критичне значення, ми відхиляємо нульову гіпотезу. Це означає, що у нас є достатньо доказів, щоб стверджувати, що справжній розподіл покупців, які відвідують цей магазин у вихідні, не дорівнює 30% у п’ятницю, 50% у суботу та 20% у неділю.

Критерій хі-квадрат на однорідність

Ми використовуємо тест хі-квадрат для однорідності, коли хочемо формально перевірити, чи є різниця в пропорціях між кількома групами.

Приклад: баскетбольний тренувальний центр хоче побачити, чи дві нові тренувальні програми підвищать частку його гравців, які пройдуть складний тест на стрільбу. 172 гравці випадковим чином розподіляються до програми 1, 173 до програми 2 і 215 до поточної програми. Після використання тренувальних програм протягом місяця гравці проходять іспит зі стрільби. У таблиці нижче показано кількість гравців, які пройшли тестування стрільби, залежно від програми, яку вони використовували.

Використовуючи рівень значущості 0,05, ми виконуємо тест хі-квадрат, щоб визначити, чи є показник успішності однаковим для кожної програми навчання.

Виявляється, статистика тесту для цього тесту хі-квадрат становить 4,208.

Тоді ми можемо знайти критичне тестове значення в таблиці розподілу хі-квадрат. Ступені свободи дорівнюють (#рядки-1) * (#стовпці-1) = (2-1) * (3-1) = 2, і проблема сказала нам, що ми повинні використовувати альфа-рівень 0,05 Отже, згідно з таблицею розподілу хі-квадрат, критичне значення критерію становить 5,991 .

Оскільки наша тестова статистика менша за наше критичне значення, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатніх доказів того, що три програми навчання дають різні результати.