Як інтерпретувати середню квадратичну помилку (rmse)
Регресійний аналіз — це техніка, яку ми можемо використати, щоб зрозуміти взаємозв’язок між однією або декількома змінними предиктора та змінною відповіді .
Один із способів оцінити, наскільки регресійна модель відповідає набору даних, — обчислити середню квадратичну помилку , яка є показником, який повідомляє нам про середню відстань між прогнозованими значеннями моделі та фактичними значеннями набору даних.
Чим нижче RMSE, тим краще дана модель здатна «відповідати» набору даних.
Формула для знаходження середньої квадратичної помилки, часто скорочена RMSE , така:
RMSE = √ Σ(P i – O i ) 2 / n
золото:
- Σ – химерний символ, який означає «сума»
- P i – прогнозоване значення для i-го спостереження в наборі даних
- O i — спостережене значення для i-го спостереження в наборі даних
- n – розмір вибірки
У наведеному нижче прикладі показано, як інтерпретувати RMSE для даної моделі регресії.
Приклад: як інтерпретувати RMSE для регресійної моделі
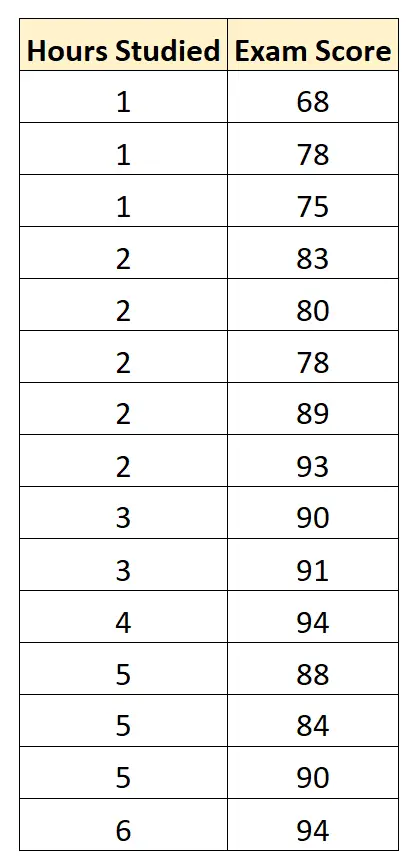
Припустімо, ми хочемо побудувати регресійну модель, яка використовує «вивчені години» для прогнозування «екзаменаційної оцінки» студентів на конкретному вступному іспиті до коледжу.
Ми збираємо такі дані для 15 студентів:
Потім ми використовуємо статистичне програмне забезпечення (наприклад, Excel, SPSS, R, Python) тощо. щоб знайти таку підігнану модель регресії:
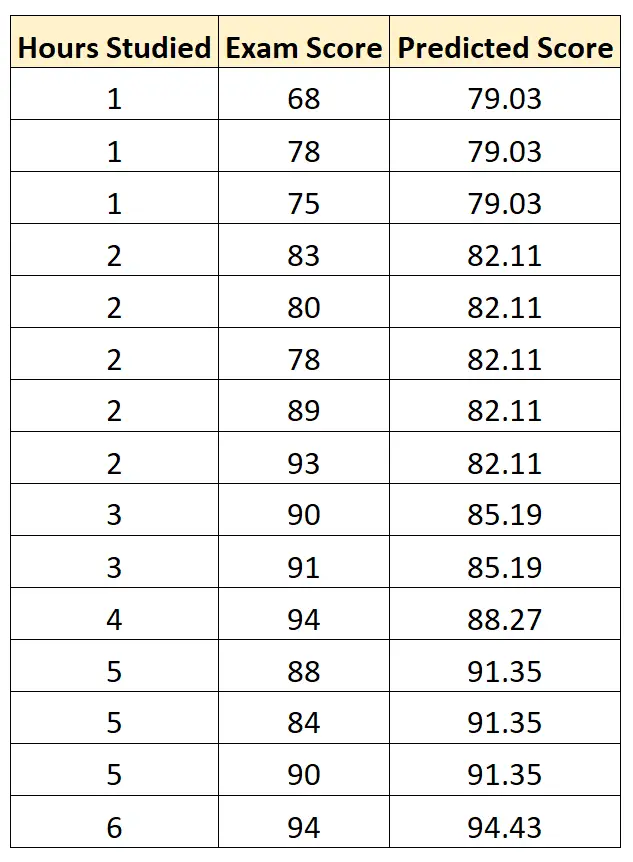
Оцінка за іспит = 75,95 + 3,08* (вивчені години)
Потім ми можемо використати це рівняння, щоб передбачити оцінку кожного студента на іспитах на основі кількості годин, які вони вивчали:
Потім ми можемо обчислити квадрат різниці між кожним передбаченим іспитовим балом і фактичним іспитовим балом. Потім ми можемо взяти квадратний корінь із середнього значення цих різниць:
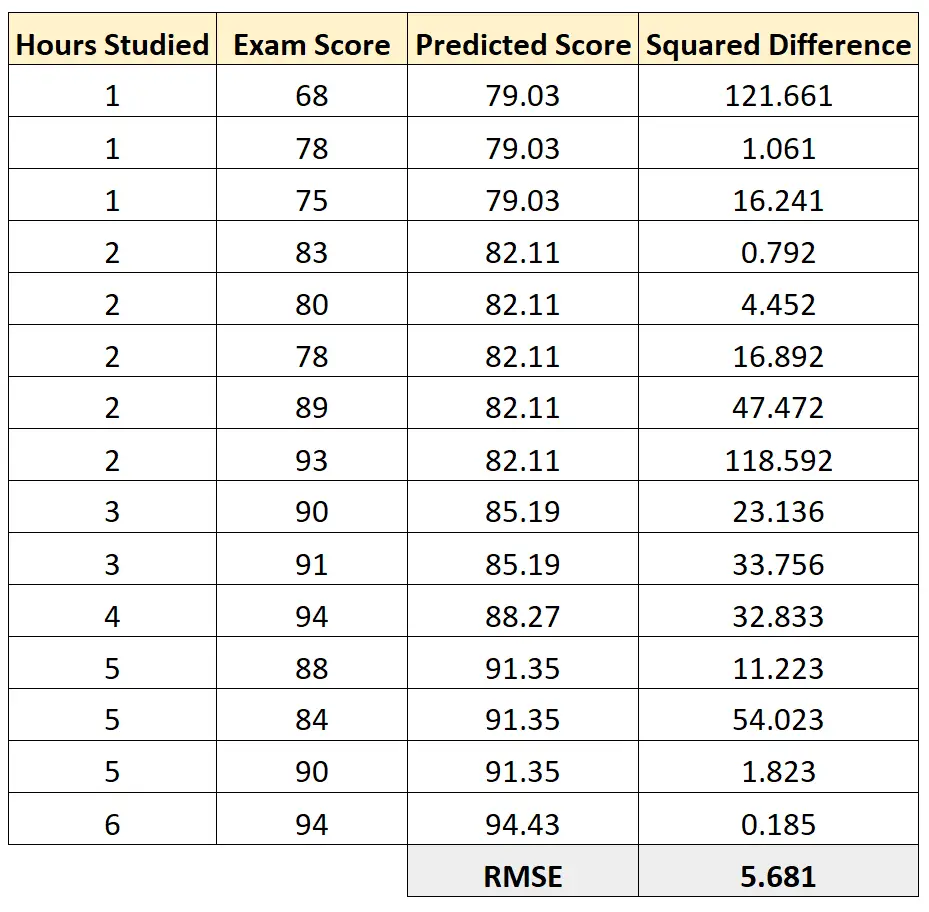
RMSE цієї моделі регресії дорівнює 5,681 .
Нагадаємо, що залишки регресійної моделі – це різниці між спостережуваними значеннями даних і прогнозованими значеннями моделі.
Залишок = (P i – O i )
золото
- P i – прогнозоване значення для i-го спостереження в наборі даних
- O i — спостережене значення для i-го спостереження в наборі даних
І пам’ятайте, що RMSE регресійної моделі обчислюється наступним чином:
RMSE = √ Σ(P i – O i ) 2 / n
Це означає, що RMSE представляє квадратний корінь із дисперсії залишків.
Це значення корисно знати, оскільки воно дає нам уявлення про середню відстань між спостережуваними значеннями даних і прогнозованими значеннями даних.
Це контрастує з R-квадратом моделі, який говорить нам, яку частину дисперсії у змінній відповіді можна пояснити змінною(ями) предиктора моделі.
Порівняння значень RMSE різних моделей
RMSE особливо корисний для порівняння відповідності різних регресійних моделей.
Наприклад, припустімо, що ми хочемо побудувати регресійну модель для прогнозування балів студентів на іспитах і хочемо знайти найкращу можливу модель серед кількох потенційних моделей.
Припустимо, ми підбираємо три різні регресійні моделі та знаходимо їм відповідні значення RMSE:
- RMSE моделі 1: 14,5
- RMSE моделі 2: 16,7
- RMSE моделі 3: 9,8
Модель 3 має найнижчий RMSE, що говорить нам про те, що вона здатна найкраще відповідати набору даних серед трьох потенційних моделей.
Додаткові ресурси
Калькулятор RMSE
Як розрахувати RMSE в Excel
Як розрахувати RMSE в R
Як обчислити RMSE в Python