Що таке ідеальна мультиколінеарність? (визначення та приклади)
У статистиці мультиколінеарність виникає, коли дві або більше змінних предикторів сильно корельовані одна з одною, так що вони не надають унікальної чи незалежної інформації в моделі регресії.
Якщо ступінь кореляції між змінними досить високий, це може спричинити проблеми під час підгонки та інтерпретації регресійної моделі.
Найбільш крайній випадок мультиколінеарності називається ідеальною мультиколінеарністю . Це відбувається, коли дві або більше змінних предиктора мають точний лінійний зв’язок одна з одною.
Наприклад, припустимо, що ми маємо такий набір даних:
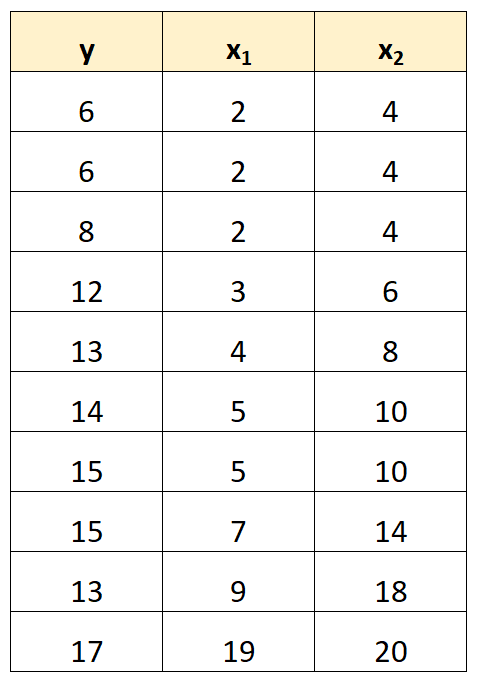
Зверніть увагу, що значення змінної предиктора x 2 є просто значеннями x 1 , помноженими на 2.
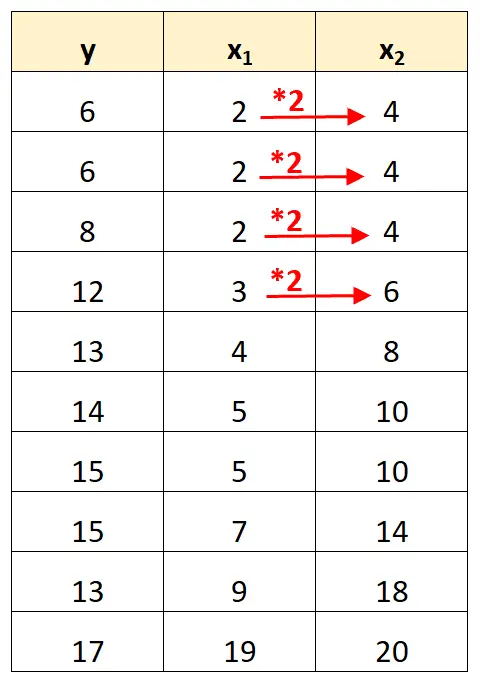
Це приклад ідеальної мультиколінеарності .
Проблема ідеальної мультиколінеарності
Коли в наборі даних присутня ідеальна мультиколінеарність, звичайні найменші квадрати не можуть дати оцінки коефіцієнтів регресії.
Дійсно, неможливо оцінити граничний вплив змінної предиктора (x 1 ) на змінну відповіді (y), зберігаючи іншу змінну предиктора (x 2 ) постійною, оскільки x 2 рухається завжди точно тоді, коли рухається x 1 .
Коротше кажучи, ідеальна мультиколінеарність унеможливлює оцінку значення для кожного коефіцієнта в моделі регресії.
Як боротися з ідеальною мультиколінеарністю
Найпростіший спосіб впоратися з ідеальною мультиколінеарністю — видалити одну зі змінних, яка має точний лінійний зв’язок з іншою змінною.
Наприклад, у нашому попередньому наборі даних ми могли просто видалити x 2 як змінну предиктора.
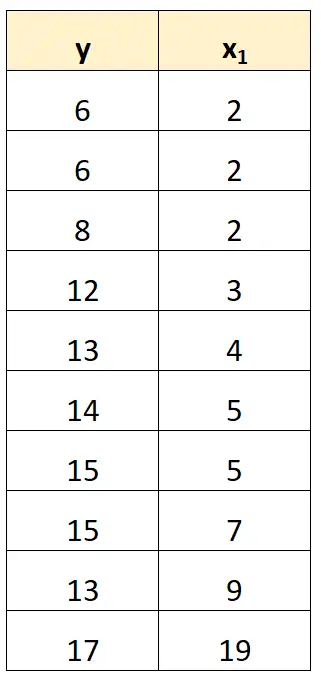
Потім ми підібрали б регресійну модель, використовуючи x 1 як змінну прогностику та y як змінну відповіді.
Приклади ідеальної мультиколінеарності
Наступні приклади демонструють три найпоширеніші сценарії ідеальної мультиколінеарності на практиці.
1. Прогностична змінна є кратною іншій
Скажімо, ми хочемо використовувати «зріст у сантиметрах» і «зріст у метрах», щоб передбачити вагу певного виду дельфінів.
Ось як може виглядати наш набір даних:
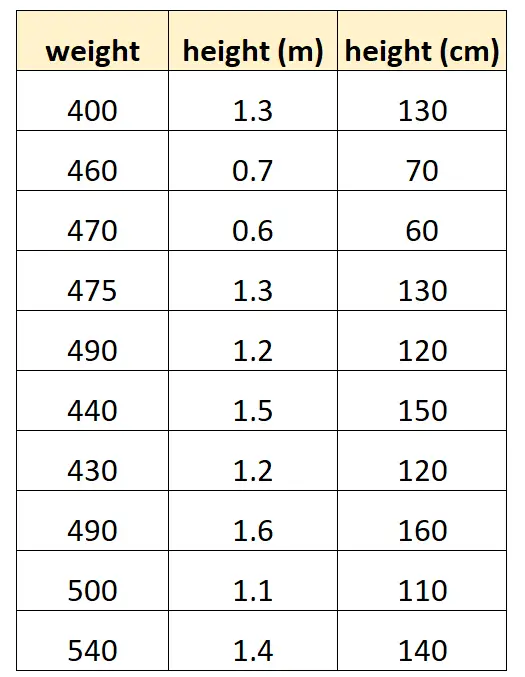
Зауважте, що значення «зростання в сантиметрах» просто дорівнює «зростанню в метрах», помноженому на 100. Це випадок ідеальної мультиколінеарності.
Якщо ми спробуємо підібрати модель множинної лінійної регресії в R за допомогою цього набору даних, ми не зможемо отримати оцінку коефіцієнта для змінної предиктора “meters”:
#define data df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540), m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4), cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140)) #fit multiple linear regression model model <- lm(weight~m+cm, data=df) #view summary of model summary(model) Call: lm(formula = weight ~ m + cm, data = df) Residuals: Min 1Q Median 3Q Max -70,501 -25,501 5,183 19,499 68,590 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 458,676 53,403 8,589 2.61e-05 *** m 9.096 43.473 0.209 0.839 cm NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 41.9 on 8 degrees of freedom Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395
2. Прогностична змінна є перетвореною версією іншої
Припустимо, ми хочемо використовувати «бали» та «бали за шкалою» для прогнозування рейтингу баскетболістів.
Припустимо, що змінна «масштабовані бали» обчислюється як:
Масштабовані бали = (балів – μ балів ) / σ балів
Ось як може виглядати наш набір даних:
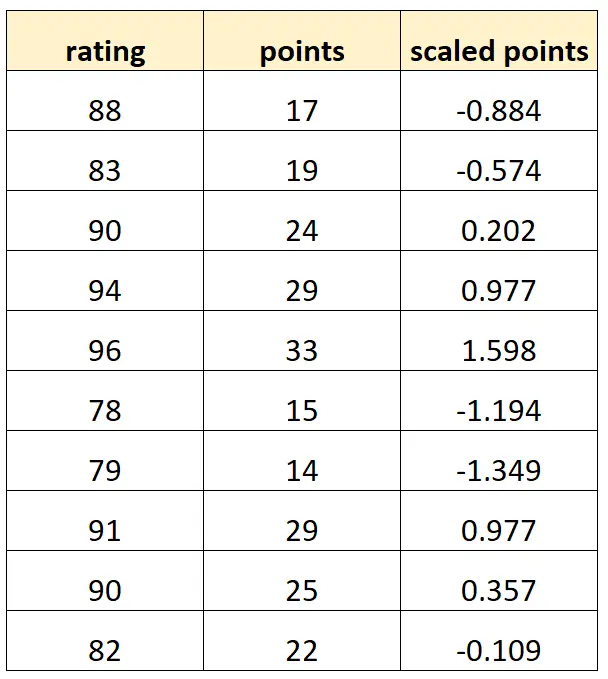
Зауважте, що кожне значення «масштабованих балів» є просто стандартизованою версією «балів». Це випадок ідеальної мультиколінеарності.
Якщо ми спробуємо підібрати модель множинної лінійної регресії в R за допомогою цього набору даних, ми не зможемо отримати оцінку коефіцієнта для змінної предиктора «масштабованих точок»:
#define data df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82), pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22)) df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts) #fit multiple linear regression model model <- lm(rating~pts+scaled_pts, data=df) #view summary of model summary(model) Call: lm(formula = rating ~ pts + scaled_pts, data = df) Residuals: Min 1Q Median 3Q Max -4.4932 -1.3941 -0.2935 1.3055 5.8412 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 67.4218 3.5896 18.783 6.67e-08 *** pts 0.8669 0.1527 5.678 0.000466 *** scaled_pts NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.953 on 8 degrees of freedom Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663
3. Фіктивна змінна пастка
Інший сценарій, за якого може виникнути ідеальна мультиколінеарність, відомий як пастка фіктивної змінної . Це коли ми хочемо взяти категоріальну змінну в моделі регресії та перетворити її на «фіктивну змінну», яка приймає значення 0, 1, 2 тощо.
Наприклад, скажімо, ми хочемо використати змінні-прогнози «вік» і «сімейний стан» для прогнозування доходу:

Щоб використовувати «сімейний стан» як прогностичну змінну, ми повинні спочатку перетворити його на фіктивну змінну.
Для цього ми можемо залишити «Неодружений» як базове значення, оскільки це трапляється найчастіше, і призначити значення 0 або 1 для «Одружений» і «Розлучений» наступним чином:

Помилкою було б створити три нові фіктивні змінні таким чином:

У цьому випадку змінна «Неодружений» є ідеальною лінійною комбінацією змінних «Одружений» і «Розлучений». Це приклад ідеальної мультиколінеарності.
Якщо ми спробуємо підібрати модель множинної лінійної регресії в R за допомогою цього набору даних, ми не зможемо отримати оцінку коефіцієнта для кожної змінної предиктора:
#define data df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107), age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53), single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0), married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1), divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0)) #fit multiple linear regression model model <- lm(income~age+single+married+divorced, data=df) #view summary of model summary(model) Call: lm(formula = income ~ age + single + married + divorced, data = df) Residuals: Min 1Q Median 3Q Max -9.7075 -5.0338 0.0453 3.3904 12.2454 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 16.7559 17.7811 0.942 0.37739 age 1.4717 0.3544 4.152 0.00428 ** single -2.4797 9.4313 -0.263 0.80018 married NA NA NA NA divorced -8.3974 12.7714 -0.658 0.53187 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 8.391 on 7 degrees of freedom Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865
Додаткові ресурси
Посібник із мультиколінеарності та VIF у регресії
Як розрахувати VIF в R
Як розрахувати VIF у Python
Як розрахувати VIF в Excel