Як побудувати інтервал прогнозу в excel

У статистиці проста лінійна регресія — це техніка, яку ми можемо використати для кількісного визначення зв’язку між змінною предиктором x і змінною відповіді y.

Коли ми виконуємо просту лінійну регресію, ми отримуємо «лінію найкращого підходу», яка описує зв’язок між x і y, яку можна записати так:

ŷ = b ₀ + b ₁ x

золото:

• ŷ – прогнозоване значення змінної відповіді
• b ₀ є точкою перетину y
• b ₁ – коефіцієнт регресії
• х – значення змінної предиктора

Іноді ми хочемо використати цю лінію найкращого підходу для побудови інтервалу прогнозу для заданого значення x ₀ , який є інтервалом навколо прогнозованого значення ŷ ₀ таким чином, що існує 95% ймовірність того, що справжнє значення y у сукупності відповідний x ₀ входить до цього інтервалу.

Формула для розрахунку інтервалу передбачення для заданого значення x ₀ записується:

ŷ ₀ +/- t _α/2,df=n-2 * se

золото:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

Формула може здатися трохи лякаючою, але насправді її легко обчислити в Excel. Далі ми побачимо приклад використання цієї формули для обчислення інтервалу передбачення для заданого значення в Excel.

Приклад: як побудувати інтервал передбачення в Excel

Наступний набір даних показує кількість вивчених годин, а також іспитовий бал, отриманий 15 різними студентами:

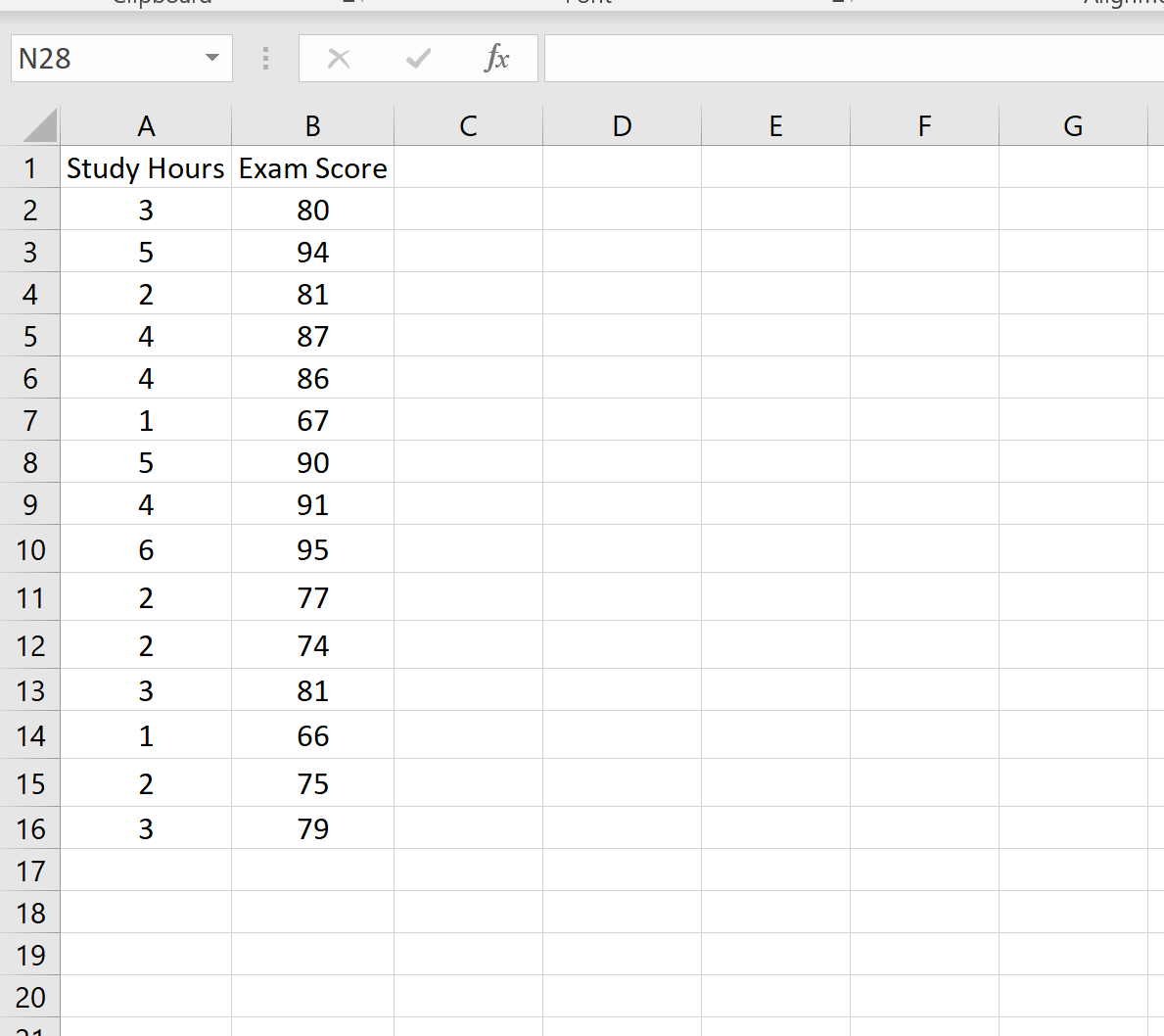
Припустімо, ми хочемо створити 95% інтервал прогнозування для значення x ₀ = 3. Тобто, ми хочемо створити такий інтервал, щоб існувала 95% ймовірність того, що оцінка іспиту потрапить у цей інтервал для студента, який навчається за 3 години.

На наступному знімку екрана показано, як обчислити всі значення, необхідні для отримання цього інтервалу передбачення.

Примітка: Формули в стовпці F показують, як були розраховані значення в стовпці E.

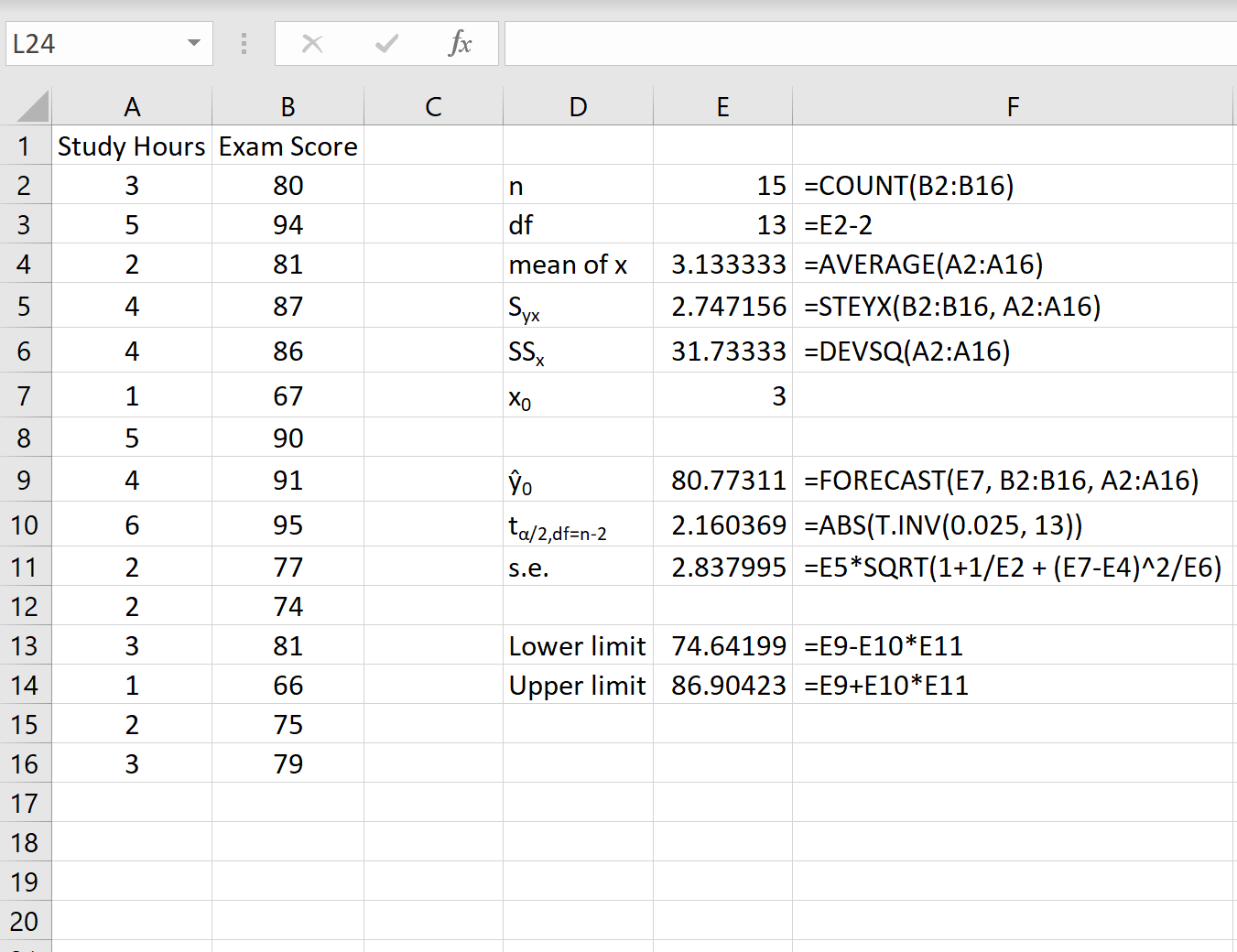
95% інтервал передбачення для значення x ₀ = 3 становить (74,64, 86,90) . Тобто ми з імовірністю 95% прогнозуємо, що студент, який навчається 3 години, отримає бал від 74,64 до 86,90.

Деякі примітки щодо використаних розрахунків:

• Щоб обчислити t-критичне значення t _α/2,df=n-2, ми використали α/2 = 0,05/2 = 0,25, оскільки нам потрібен інтервал передбачення 95%. Зауважте, що вищі інтервали передбачення (наприклад, 99% інтервал передбачення) призведуть до ширших інтервалів. І навпаки, менший інтервал передбачення (наприклад, 90% інтервал передбачення) призведе до більш вузького інтервалу.
• Ми використали формулу =ПРОГНОЗ() , щоб отримати прогнозоване значення для ŷ ₀ , але формула =ПРОГНОЗ.ЛІНЕЙНИЙ() поверне точно таке саме значення.