Повний посібник: як інтерпретувати результати anova у sas

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

У наступному прикладі показано, як інтерпретувати результати одностороннього дисперсійного аналізу в SAS.

Приклад: інтерпретація результатів ANOVA у SAS

Припустімо, що дослідник набирає 30 студентів для участі в дослідженні. Для підготовки до іспиту студенти випадковим чином розподіляються для використання одного з трьох методів навчання.

Результати іспитів для кожного студента наведено нижче:

Ми можемо використати такий код, щоб створити цей набір даних у SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Далі ми використаємо proc ANOVA для виконання одностороннього ANOVA:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Примітка . Ми використали оператор середнього значення разом із опціями tukey та cldiff , щоб вказати, що слід виконувати тест Tukey post-hoc (з довірчими інтервалами), якщо загальне значення p від одностороннього дисперсійного аналізу є статистично значущим.

Спочатку ми розглянемо таблицю ANOVA в результаті:

Ось як інтерпретувати кожне значення у виводі:

Модель DF: Ступені свободи для методу змінних. Це обчислюється як #groups -1. У цьому випадку було 3 різні методи дослідження, тому це значення: 3-1 = 2 .

Помилка DF: ступені свободи для залишків. Це обчислюється як #загальна кількість спостережень – #групи. У цьому випадку було 24 спостереження і 3 групи, тому це значення: 24-3 = 21 .

Виправлений підсумок : сума моделі DF і помилки DF. Це значення дорівнює 2 + 21 = 23 .

Модель суми квадратів: сума квадратів, пов’язана з методом змінної. Це значення дорівнює 175,583 .

Помилка суми квадратів: сума квадратів, пов’язана із залишками або «помилками». Це значення становить 350,25 .

Усього виправленої суми квадратів : сума моделі SS і помилки SS. Це значення дорівнює 525,833 .

Модель середніх квадратів: середня сума квадратів, пов’язана з методом . Це обчислюється як модель SS / модель DF, або 175,583 / 2 = 87,79 .

Середня квадратична помилка: середня сума квадратів, пов’язаних із залишками. Це обчислюється як SS Error / DF Error, що становить 350,25 / 21 = 16,68 .

Значення F: загальна F-статистика моделі ANOVA. Це обчислюється як середньоквадратичне значення моделі/середньоквадратична помилка, або 87,79/16,68 = 5,26 .

Pr >F: значення p, пов’язане зі статистикою F із чисельником df = 2 і знаменником df = 21. У цьому випадку значення p дорівнює 0,0140 .

Найважливішим значенням у наборі результатів є p-значення, оскільки воно говорить нам, чи є значна різниця в середніх значеннях між трьома групами.

Нагадаємо, що односторонній дисперсійний аналіз використовує такі нульові та альтернативні гіпотези:

• H ₀ (нульова гіпотеза): усі групові середні рівні.
• H _A (альтернативна гіпотеза): принаймні одне групове середнє значення відрізняється від інших.

Оскільки p-значення в нашій таблиці ANOVA (0,0140) менше 0,05, ми відхиляємо нульову гіпотезу.

Це означає, що ми маємо достатньо доказів, щоб стверджувати, що середній бал іспиту не є однаковим для трьох методів навчання.

Щоб точно визначити, які групові середні відрізняються, нам потрібно звернутися до таблиці остаточних результатів, яка показує результати пост-хок тестів Тьюкі:

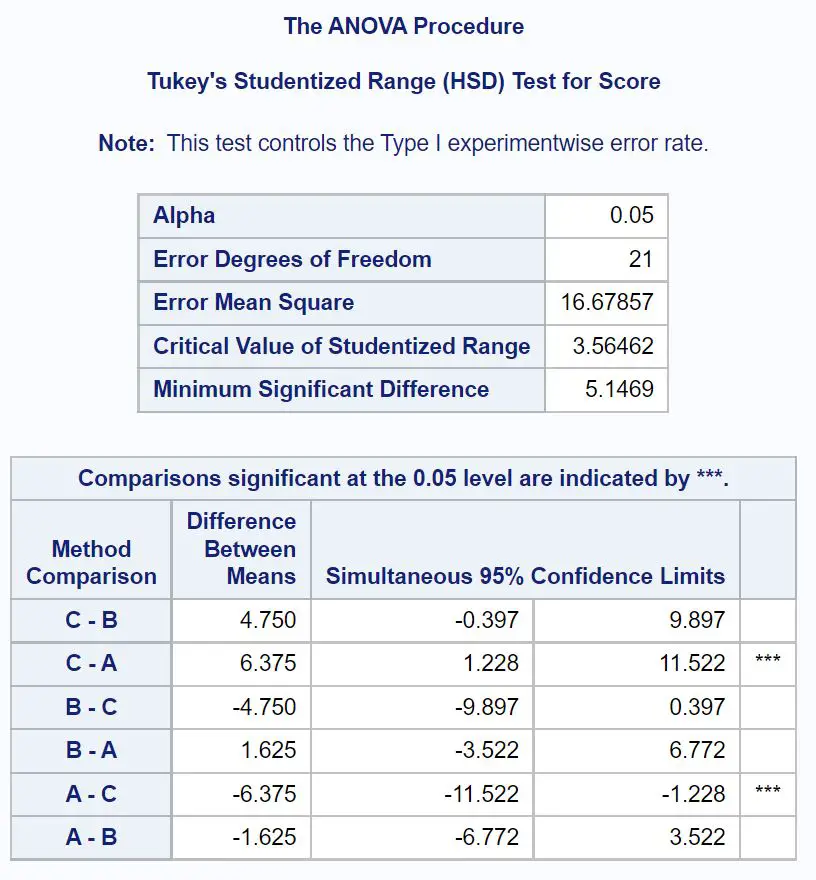
Щоб з’ясувати, які середні групи відрізняються, нам потрібно подивитися, які парні порівняння мають зірочки ( *** ).

Таблиця показує, що існує статистично значуща різниця в середніх балах за іспит між групою А та групою С.

Зокрема, середня різниця в іспитових балах між групою С і групою А становить 6,375 .

95% довірчий інтервал для середньої різниці становить [1,228, 11,522] .

Статистично значущих відмінностей між середніми показниками інших груп немає.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про моделі ANOVA:

Посібник із використання пост-хок тестування з ANOVA
Як виконати односторонній дисперсійний аналіз у SAS
Як виконати двосторонній дисперсійний аналіз у SAS