Comment effectuer une analyse des composantes principales dans SAS

L’analyse en composantes principales (ACP) est une technique d’apprentissage automatique non supervisée qui cherche à trouver les composantes principales – des combinaisons linéaires de variables prédictives – qui expliquent une grande partie de la variation dans un ensemble de données.

Le moyen le plus simple d’effectuer une PCA dans SAS consiste à utiliser l’instruction PROC PRINCOMP , qui utilise la syntaxe de base suivante :

proc princomp data=my_data out=out_data outstat=stats;
    var var1 var2 var3;
run;

Voici ce que fait chaque instruction :

• data : Le nom de l’ensemble de données à utiliser pour la PCA
• out : Le nom de l’ensemble de données à créer qui contient toutes les données d’origine ainsi que les scores des composants principaux
• outstat : Spécifie qu’un ensemble de données doit être créé contenant les moyennes, les écarts types, les coefficients de corrélation, les valeurs propres et les vecteurs propres.
• var : les variables à utiliser pour la PCA à partir de l’ensemble de données d’entrée.

L’exemple étape par étape suivant montre comment utiliser l’instruction PROC PRINCOMP en pratique pour effectuer une analyse des composants principaux dans SAS.

Étape 1 : Créer un ensemble de données

Supposons que nous disposions de l’ensemble de données suivant contenant diverses informations sur 20 joueurs de basket-ball :

/*create dataset*/
data my_data;
    input points assists rebounds;
    datalines;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run;

/*view dataset*/
proc print data=my_data;

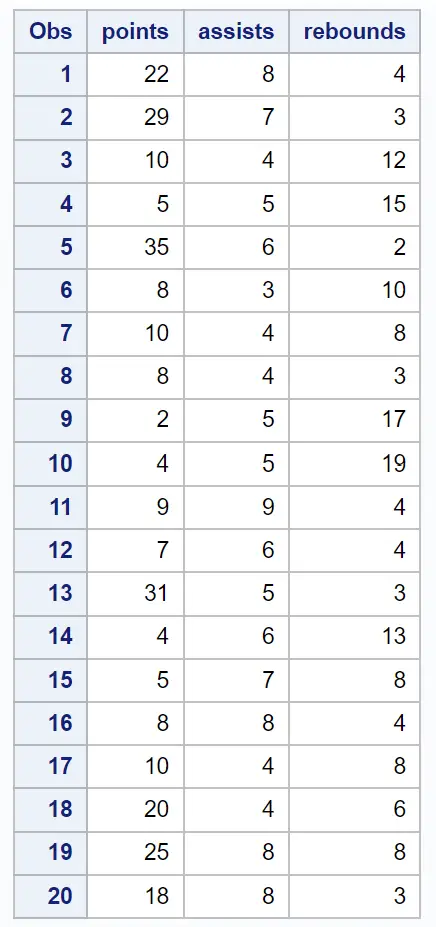
Étape 2 : Effectuer une analyse des composantes principales

Nous pouvons utiliser l’instruction PROC PRINCOMP pour effectuer une analyse en composantes principales à l’aide des variables points , assistances et rebonds de l’ensemble de données :

/*perform principal components analysis*/
proc princomp data=my_data out=out_data outstat=stats;
    var points assists rebounds;
run;

La première partie du résultat affiche diverses statistiques descriptives, notamment la moyenne et les écarts types de chaque variable d’entrée, une matrice de corrélation et les valeurs des valeurs propres et des vecteurs propres :

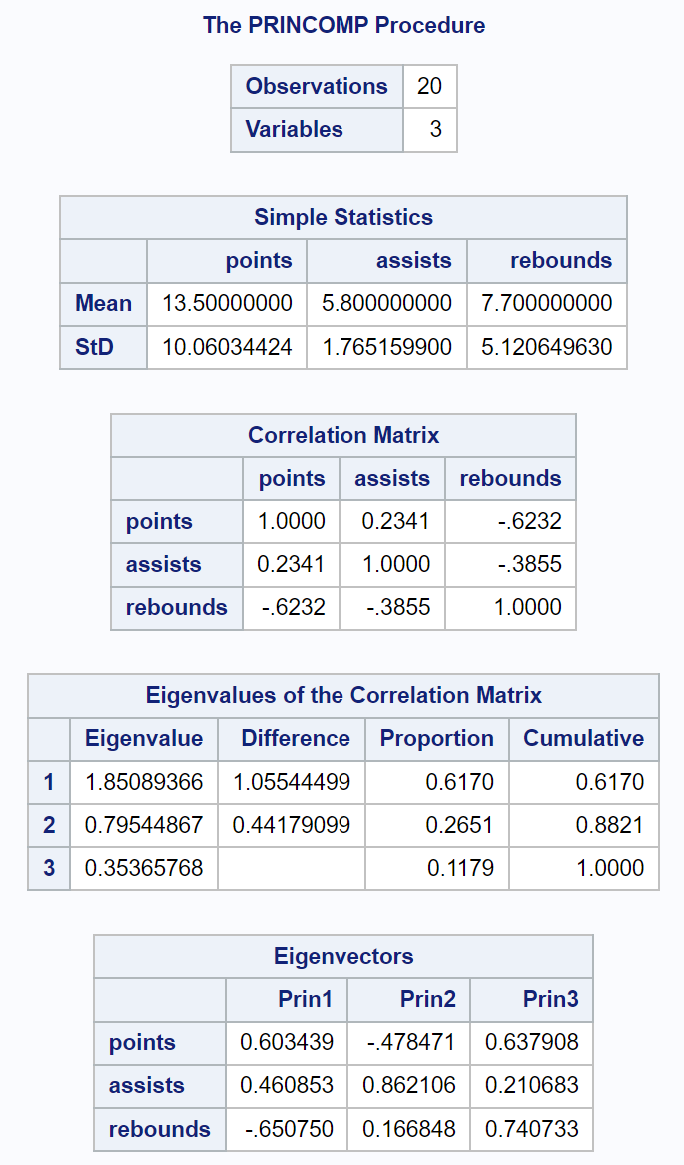
La partie suivante de la sortie affiche un tracé d’éboulis et un tracé de variance expliquée :

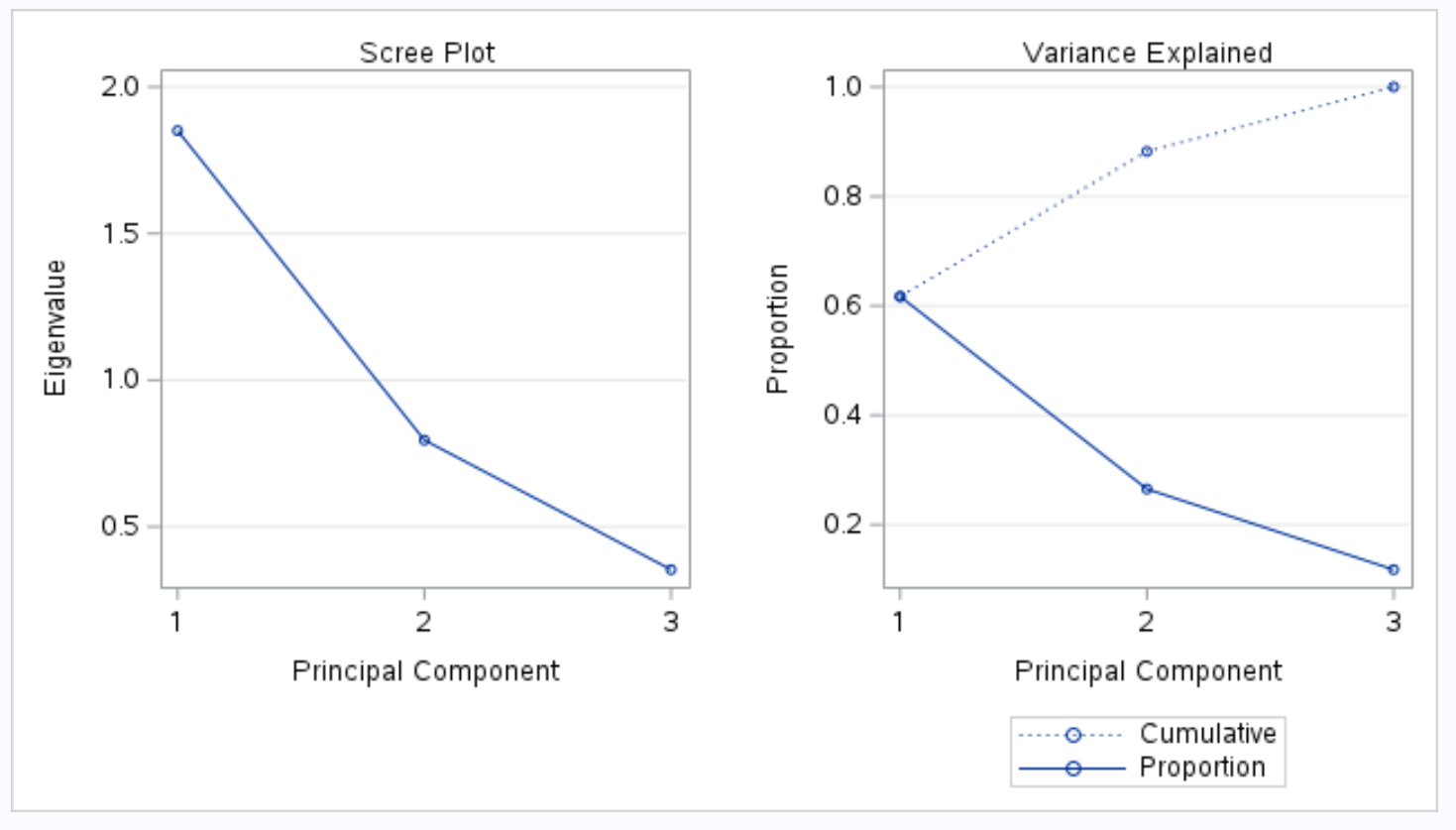
Lorsque nous effectuons une PCA, nous souhaitons souvent comprendre quel pourcentage de la variation totale de l’ensemble de données peut être expliqué par chaque composante principale.

Le tableau du résultat intitulé Valeurs propres de la matrice de corrélation nous permet de voir exactement quel pourcentage de la variation totale est expliqué par chaque composante principale :

• La première composante principale explique 61,7 % de la variation totale de l’ensemble de données.
• La deuxième composante principale explique 26,51 % de la variation totale de l’ensemble de données.
• La troisième composante principale explique 11,79 % de la variation totale de l’ensemble de données.

Notez que tous les pourcentages totalisent 100 %.

Le tracé intitulé Variance Explained nous permet ensuite de visualiser ces valeurs.

L’axe des x affiche la composante principale et l’axe des y affiche le pourcentage de la variance totale expliquée par chaque composante principale individuelle.

Étape 3 : Créer un biplot pour visualiser les résultats

Pour visualiser les résultats de l’ACP pour un ensemble de données donné, nous pouvons créer un biplot , qui est un tracé qui affiche chaque observation d’un ensemble de données sur un plan formé par les deux premiers composants principaux.

Nous pouvons utiliser la syntaxe suivante dans SAS pour créer un biplot :

/*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run;

/*create biplot using values from first two principal components*/
proc sgplot data=biplot_data;
    scatter x=Prin1 y=Prin2 / datalabel=obs;
run;

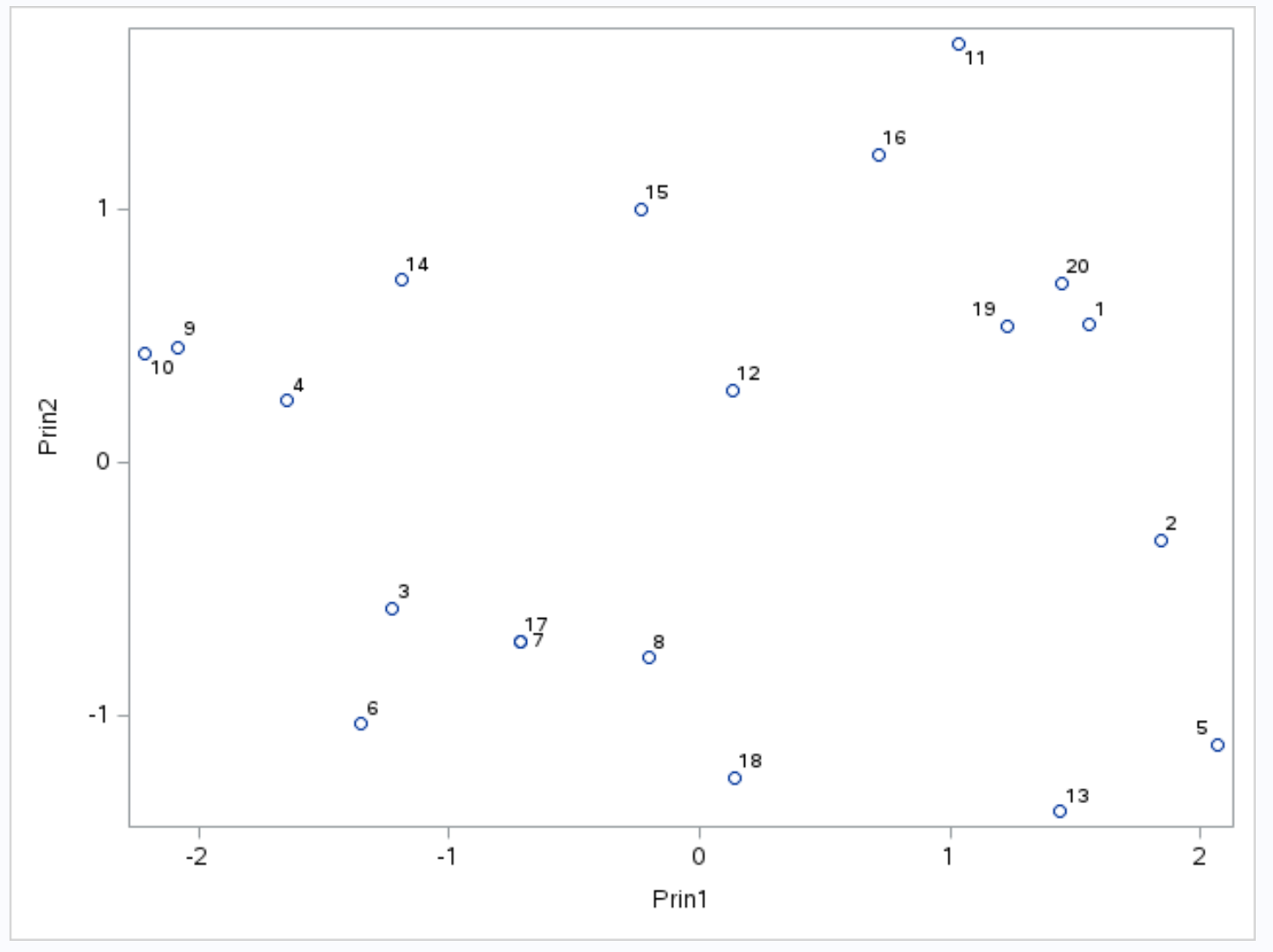
L’axe des x affiche la première composante principale, l’axe des y affiche la deuxième composante principale et les observations individuelles de l’ensemble de données sont affichées à l’intérieur du graphique sous forme de petits cercles.

Les observations qui sont côte à côte sur le graphique ont des valeurs similaires pour les trois variables de points , de passes décisives et de rebonds .

Par exemple, à l’extrême gauche du graphique, nous pouvons voir que les observations n°9 et n°10 sont extrêmement proches l’une de l’autre.

Si nous nous référons à l’ensemble de données d’origine, nous pouvons voir les valeurs suivantes pour ces observations :

• Constat n°9 : 2 points, 5 passes décisives, 17 rebonds
• Constat #10 : 4 points, 5 passes, 19 rebonds

Les valeurs sont similaires pour chacune des trois variables, ce qui explique pourquoi ces observations sont si proches les unes des autres sur le biplot.

Nous avons également vu dans le tableau du résultat intitulé Valeurs propres de la matrice de corrélation que les deux premières composantes principales représentent 88,21 % de la variation totale de l’ensemble de données.

Étant donné que ce pourcentage est très élevé, il est valable d’analyser quelles observations du biplot sont proches les unes des autres, car les deux composants principaux qui composent le biplot représentent la quasi-totalité de la variation de l’ensemble de données.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment effectuer une régression linéaire simple dans SAS
Comment effectuer une régression linéaire multiple dans SAS
Comment effectuer une régression logistique dans SAS