Comment lire une matrice de covariance

La covariance est une mesure de la façon dont les changements dans une variable sont associés aux changements dans une deuxième variable. Plus précisément, il s’agit d’une mesure du degré auquel deux variables sont linéairement associées.

Une matrice de covariance est une matrice carrée qui montre la covariance entre de nombreuses variables différentes. Cela peut être un moyen utile de comprendre comment les différentes variables sont liées dans un ensemble de données.

L’exemple suivant montre comment lire une matrice de covariance en pratique.

Comment lire une matrice de covariance

Supposons que nous ayons la matrice de covariance suivante qui contient des informations sur les résultats des examens pour trois matières différentes pour les étudiants :

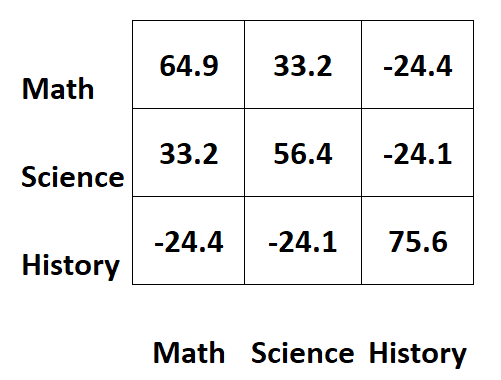
Les valeurs le long des diagonales de la matrice représentent les variances de chaque sujet.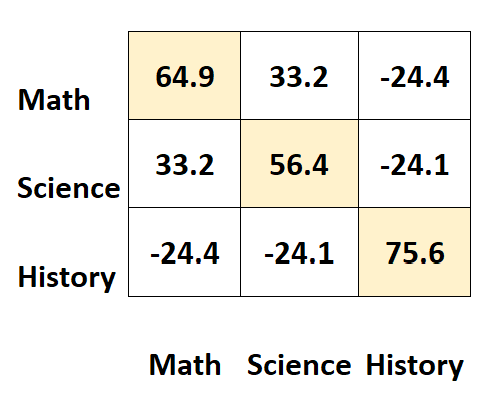

Par exemple:

• La variance des résultats en mathématiques est de 64,9 .
• La variance des scores en sciences est de 56,4 .
• La variance des scores historiques est de 75,6 .

Les autres valeurs de la matrice représentent les covariances entre les différents sujets.

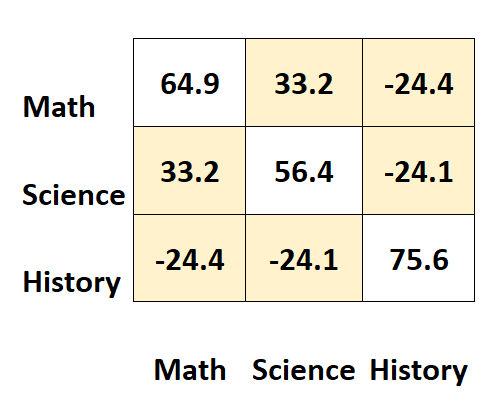
Par exemple:

• La covariance entre les scores en mathématiques et en sciences est de 33,2 .
• La covariance entre les scores en mathématiques et en histoire est de – 24,4 .
• La covariance entre les scores en sciences et en histoire est de – 24,1 .

Un nombre positif pour la covariance indique que deux variables ont tendance à augmenter ou diminuer en tandem.

Par exemple, les mathématiques et les sciences ont une covariance positive ( 33,2 ), ce qui indique que les élèves qui obtiennent des résultats élevés en mathématiques ont également tendance à obtenir des résultats élevés en sciences.

À l’inverse, les élèves qui obtiennent de faibles résultats en mathématiques ont également tendance à obtenir de faibles résultats en sciences.

Un nombre négatif pour la covariance indique que lorsqu’une variable augmente, une deuxième variable a tendance à diminuer.

Par exemple, les mathématiques et l’histoire ont une covariance négative ( -24,44 ), ce qui indique que les élèves qui obtiennent des résultats élevés en mathématiques ont tendance à avoir des résultats faibles en histoire.

À l’inverse, les élèves qui obtiennent de faibles résultats en mathématiques ont tendance à obtenir des résultats élevés en histoire.

Une note sur la symétrie d’une matrice de covariance

Il convient de noter qu’une matrice de covariance est parfaitement symétrique.

Par exemple, la cellule en haut à droite affiche exactement la même valeur que la cellule en bas à gauche :

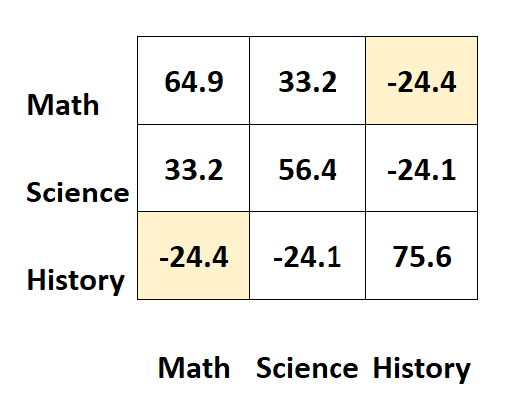
En effet, les deux cellules mesurent la covariance entre l’histoire et les mathématiques.

Une matrice de covariance étant symétrique, la moitié des valeurs de covariance affichées dans la matrice sont redondantes et inutiles.

Ainsi, parfois seule la moitié de la matrice de covariance sera affichée :

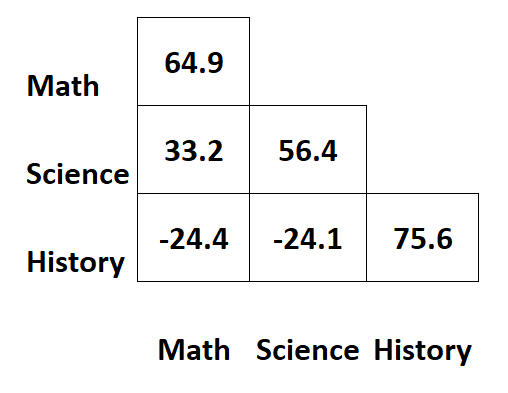
Quand utiliser une matrice de covariance

En pratique, vous aurez souvent besoin de créer et d’interpréter une matrice de corrélation plus souvent qu’une matrice de covariance.

Cependant, les matrices de covariance sont souvent utilisées « sous le capot » pour différents algorithmes et modèles d’apprentissage automatique.

Par exemple, la matrice de covariance est utilisée lors de l’ analyse des composantes principales , ce qui nous aide à comprendre les modèles sous-jacents dans un ensemble de données contenant un grand nombre de variables.

Ressources additionnelles

Les tutoriels suivants expliquent comment créer une matrice de covariance à l’aide de différents logiciels statistiques :

Comment créer une matrice de covariance dans R
Comment créer une matrice de covariance en Python
Comment créer une matrice de covariance dans SPSS
Comment créer une matrice de covariance dans Excel