Qu’est-ce qui est considéré comme un bon ou un mauvais complot résiduel ?

Dans l’analyse de régression, un tracé des résidus est un type de tracé qui affiche les valeurs ajustées d’un modèle de régression sur l’axe des x et les résidus du modèle le long de l’axe des y.

Lors de l’inspection visuelle d’un tracé résiduel, nous recherchons généralement deux éléments pour déterminer si le tracé est « bon » ou « mauvais » :

1. Les résidus présentent-ils une tendance claire ?

• Dans un « bon » tracé des résidus, les résidus ne présentent aucune tendance claire.
• Dans un « mauvais » tracé des résidus, les résidus présentent un certain type de motif tel qu’une courbe ou une vague. Cela indique que le modèle de régression que nous avons utilisé ne fournit pas un ajustement approprié aux données.

2. Les résidus augmentent-ils ou diminuent-ils en variance de manière systématique ?

• Dans un « bon » tracé des résidus, les résidus sont dispersés de manière aléatoire autour de zéro sans augmentation ni diminution systématique de la variance.
• Dans un « mauvais » tracé des résidus, la variance des résidus augmente ou diminue de manière systématique.

Si un tracé résiduel est jugé « bon », cela signifie que nous pouvons faire confiance aux résultats du modèle de régression et qu’il est possible d’interpréter les coefficients du modèle en toute sécurité.

Cependant, si un tracé résiduel est jugé « mauvais », cela signifie que les résultats du modèle ne sont pas fiables et que nous devons adapter un modèle de régression différent aux données.

Les exemples suivants expliquent comment interpréter les « bons » et les « mauvais tracés résiduels dans la pratique.

Exemple 1 : un « bon » tracé résiduel

Supposons que nous ajustions un modèle de régression et que nous obtenions le tracé résiduel suivant :

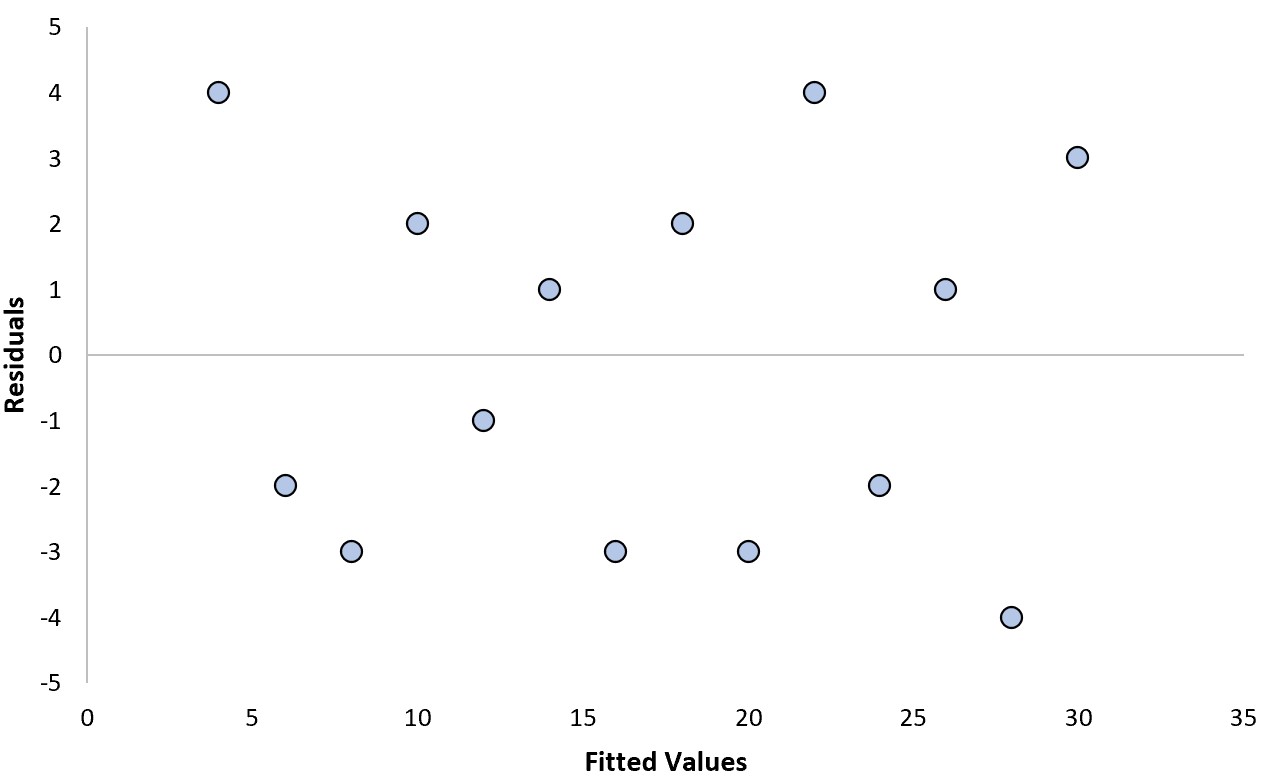
Nous pouvons répondre aux deux questions suivantes pour déterminer s’il s’agit d’une « bonne » intrigue résiduelle :

1. Les résidus présentent-ils une tendance claire ?

Non . Les résidus sont dispersés de manière aléatoire autour de zéro, sans motif clair.

2. Les résidus augmentent-ils ou diminuent-ils en variance de manière systématique ?

Non . Les résidus ont une variance assez constante (c’est-à-dire la distance entre les résidus et la valeur zéro) à chaque niveau des valeurs ajustées.

Puisque nous avons répondu « Non » à ces deux questions, nous considérerions qu’il s’agit d’une « bonne » intrigue résiduelle.

Par conséquent, nous pouvons faire confiance aux résultats du modèle de régression et interpréter les coefficients du modèle en toute sécurité.

Exemple 2 : un « mauvais » tracé résiduel avec un modèle clair

Supposons que nous ajustions un modèle de régression et que nous obtenions le tracé résiduel suivant :

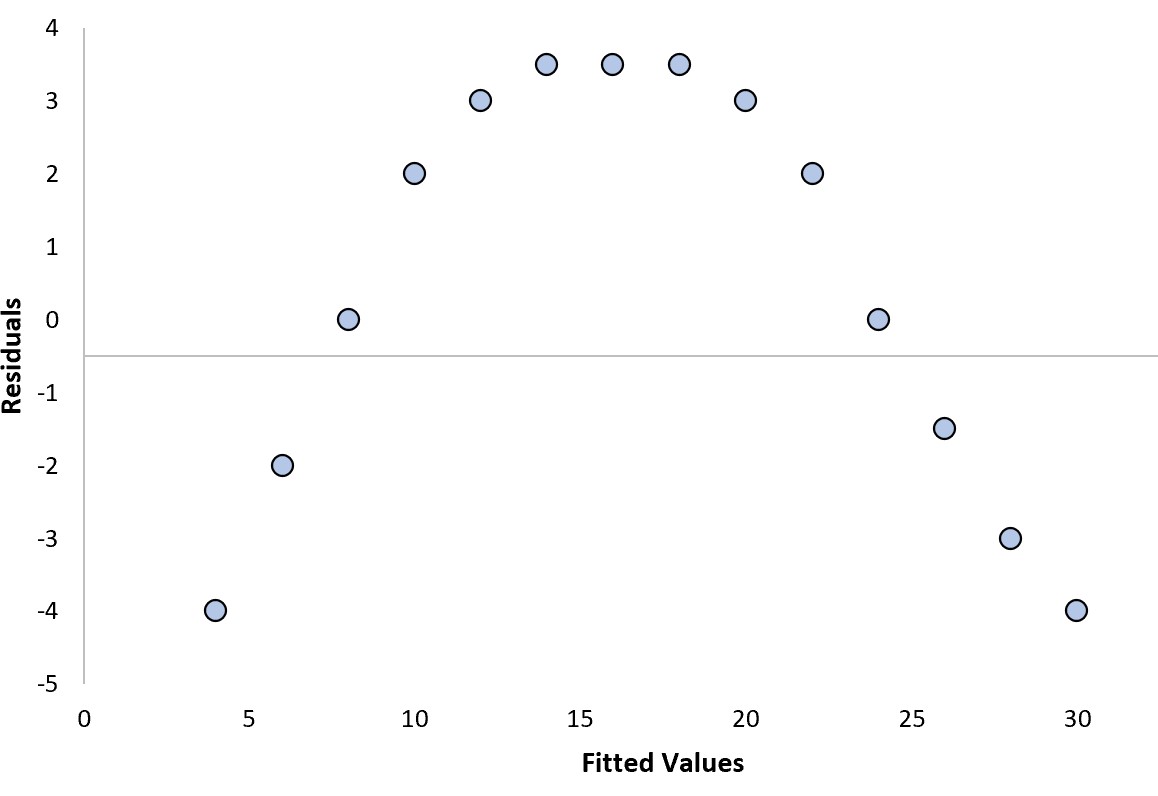
Nous pouvons répondre aux deux questions suivantes pour déterminer s’il s’agit d’une « bonne » intrigue résiduelle :

1. Les résidus présentent-ils une tendance claire ?

Oui . Les résidus présentent un motif incurvé.

2. Les résidus augmentent-ils ou diminuent-ils en variance de manière systématique ?

Oui . Les résidus ont différents niveaux de variance à différents niveaux des valeurs ajustées.

Puisque nous avons répondu « Oui » à au moins une de ces questions, nous considérerions qu’il s’agit d’une « mauvaise » intrigue résiduelle.

Cela signifie que le modèle de régression ne fournit pas un bon ajustement aux données.

En particulier, le motif incurvé dans le tracé des résidus indique qu’un modèle de régression linéaire ne parvient pas à ajuster les données et qu’un modèle de régression quadratique ferait probablement un meilleur travail.

Exemple 3 : un « mauvais » tracé résiduel avec une variance croissante

Supposons que nous ajustions un modèle de régression et que nous obtenions le tracé résiduel suivant :

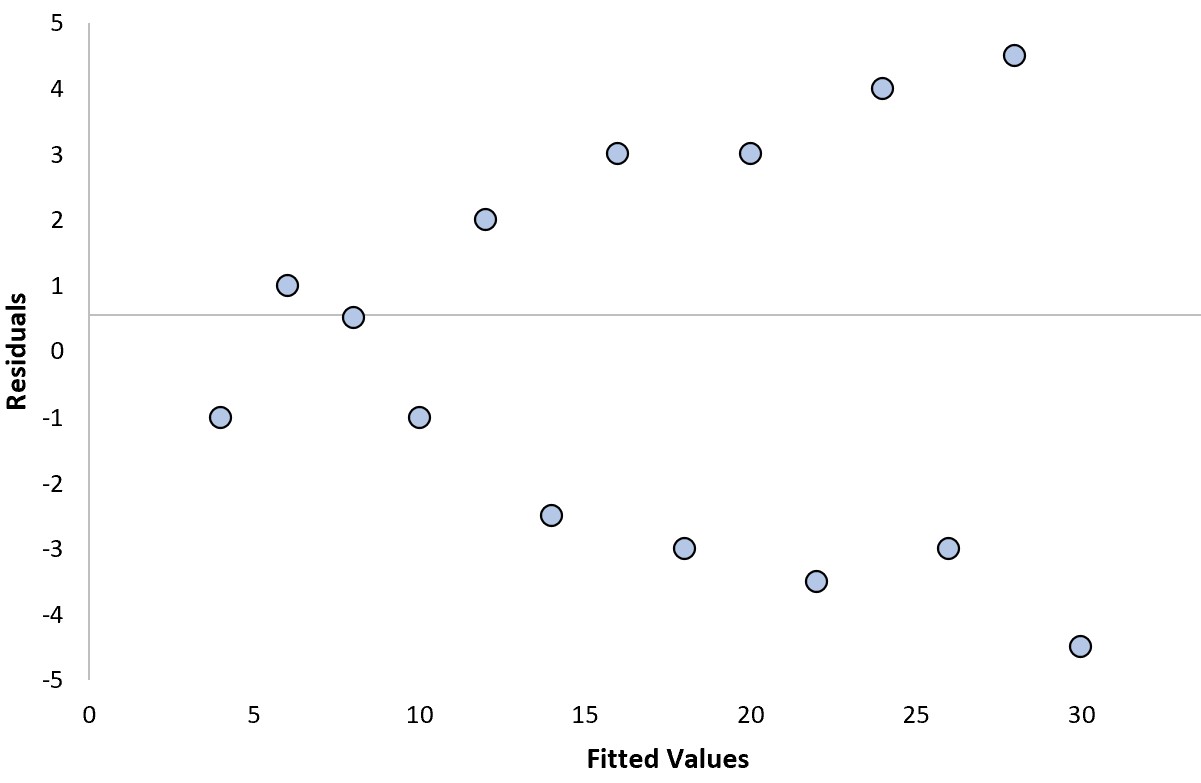
Nous pouvons répondre aux deux questions suivantes pour déterminer s’il s’agit d’une « bonne » intrigue résiduelle :

1. Les résidus présentent-ils une tendance claire ?

Non . Il n’y a pas de tendance claire dans les résidus.

2. Les résidus augmentent-ils ou diminuent-ils en variance de manière systématique ?

Oui . La variance des résidus augmente à mesure que les valeurs ajustées augmentent.

Puisque nous avons répondu « Oui » à au moins une de ces questions, nous considérerions qu’il s’agit d’une « mauvaise » intrigue résiduelle.

Dans cet exemple particulier, les résidus souffrent d’ hétéroscédasticité , qui fait référence à une variance inégale des résidus à différents niveaux des valeurs ajustées.

Cela signifie que les résultats du modèle de régression peuvent ne pas être fiables.

Reportez-vous à cet article pour découvrir différentes manières de résoudre le problème de l’hétéroscédasticité dans un modèle de régression.

Ressources additionnelles

Les didacticiels suivants expliquent comment créer des tracés de résidus à l’aide de différents logiciels statistiques :

Comment créer un tracé résiduel dans R
Comment créer un tracé résiduel en Python
Comment créer un tracé résiduel dans Excel
Comment créer un tracé résiduel dans SAS