Comment créer une ligne de meilleur ajustement dans Excel

En statistiques, une droite de meilleur ajustement est la droite qui « correspond » le mieux ou décrit la relation entre une variable prédictive et une variable de réponse .

L’exemple suivant, étape par étape, montre comment créer une ligne la mieux ajustée dans Excel.

Étape 1 : Saisissez les données

Tout d’abord, entrons dans l’ensemble de données suivant qui montre le nombre d’heures passées à s’entraîner et le total de points marqués par huit joueurs de basket différents :

Étape 2 : Créer un nuage de points

Créons ensuite un nuage de points pour visualiser la relation entre les deux variables.

Pour ce faire, mettez en surbrillance les cellules de la plage A2:B9 , puis cliquez sur l’onglet Insérer le long du ruban supérieur, puis cliquez sur l’option intitulée Dispersion dans le groupe Graphiques :

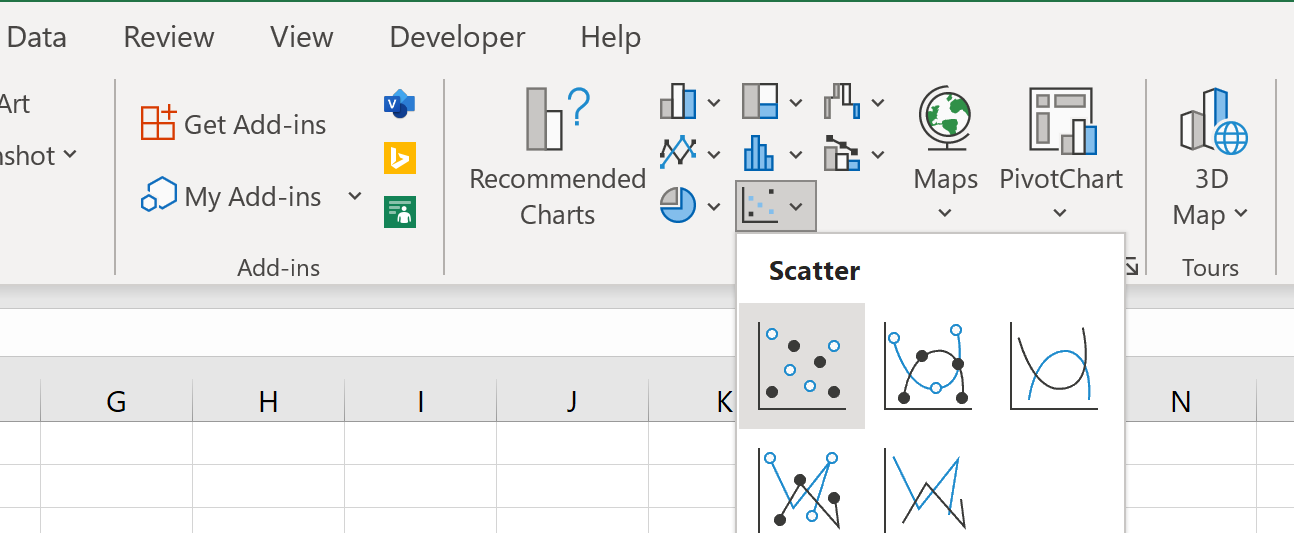
Le nuage de points suivant sera automatiquement créé :

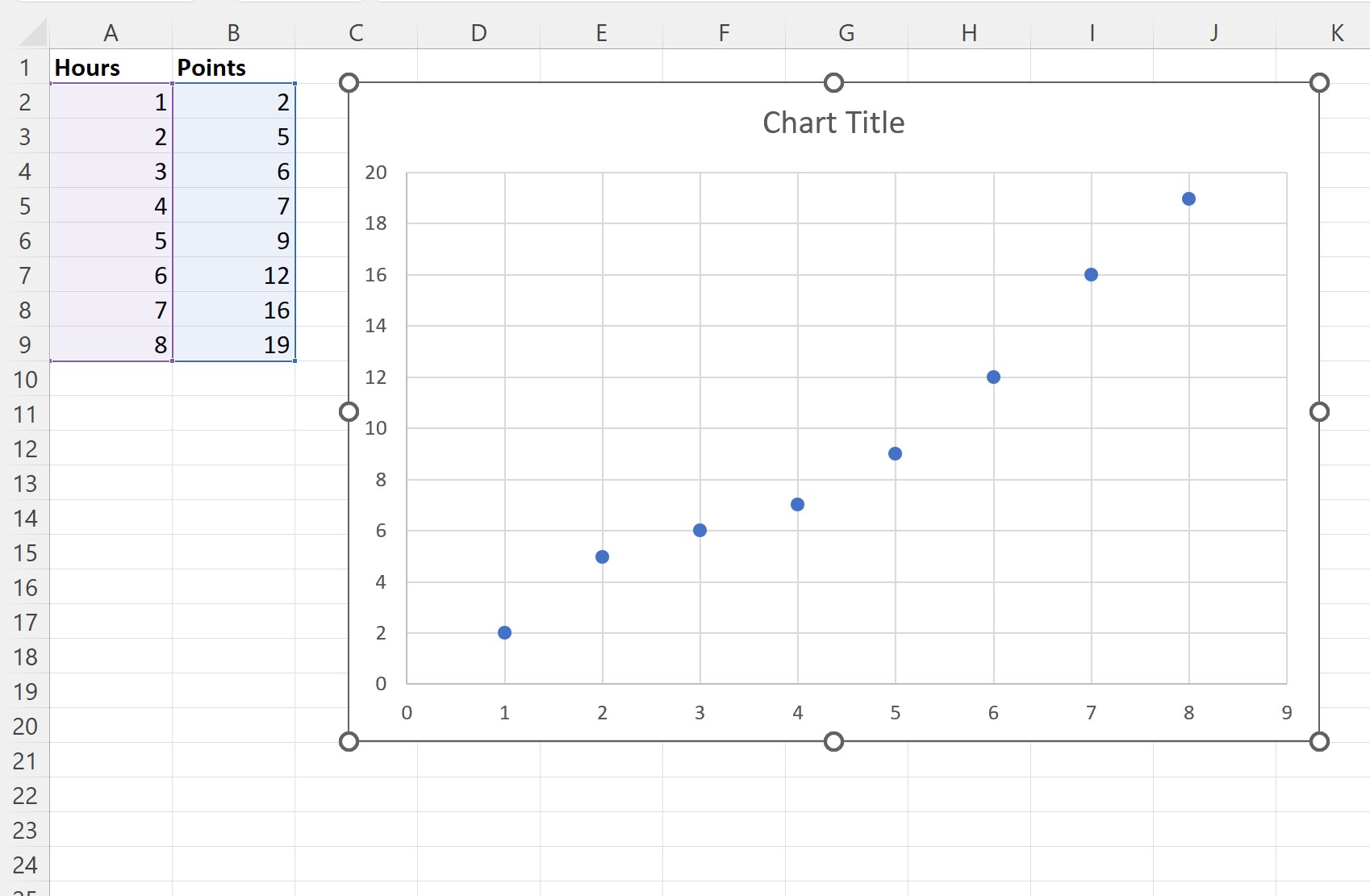
Étape 3 : Ajouter la ligne la mieux adaptée

Pour ajouter une ligne la mieux ajustée au nuage de points, cliquez n’importe où sur le graphique, puis cliquez sur le signe vert plus (+) qui apparaît dans le coin supérieur droit du graphique.

Cliquez ensuite sur la flèche à côté de Trendline , puis cliquez sur Plus d’options :

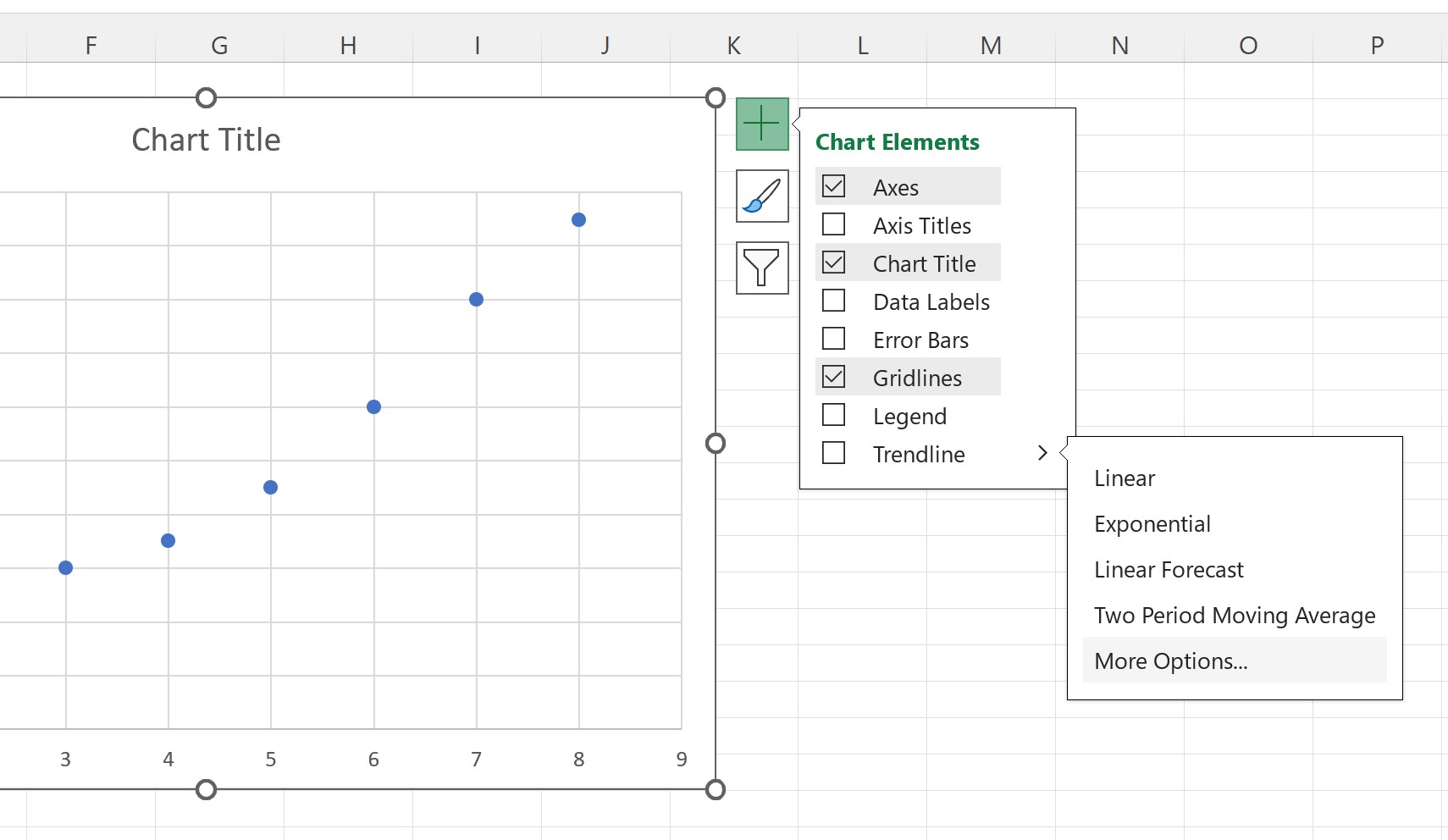
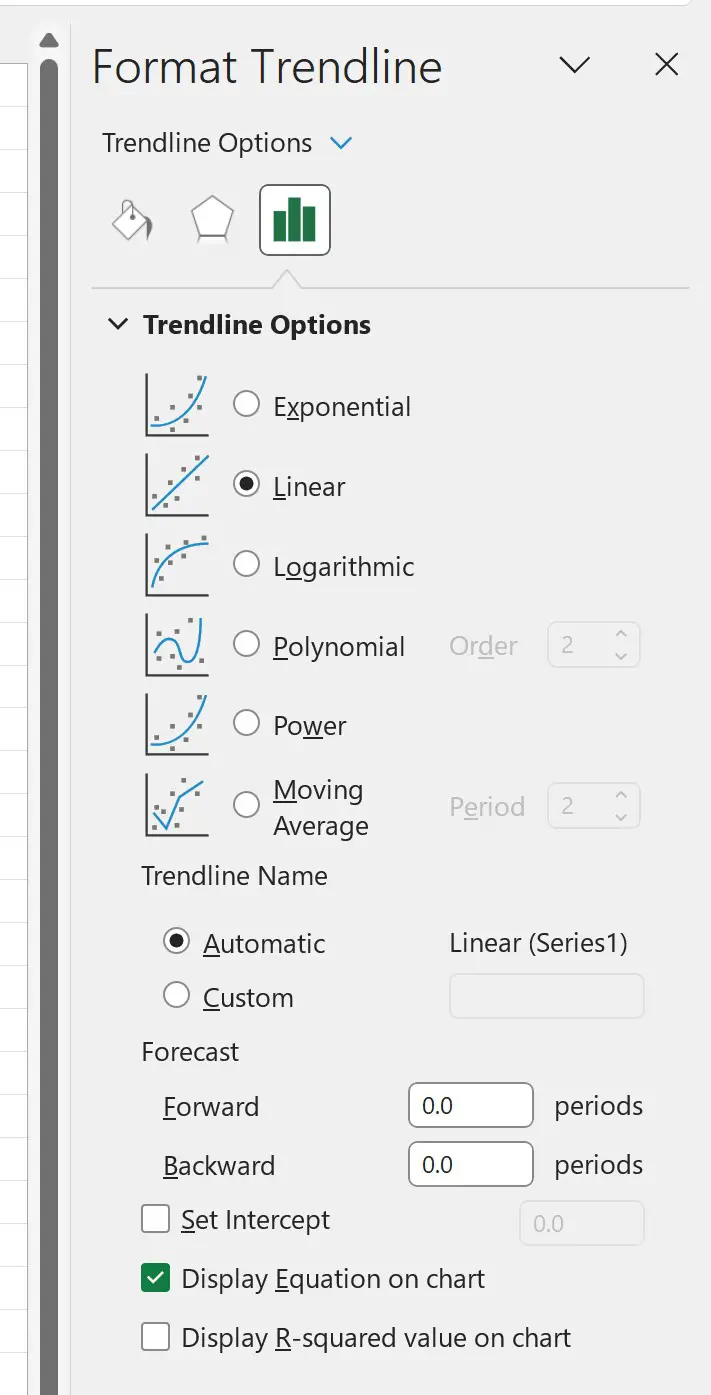
Dans le panneau Format de la ligne de tendance qui apparaît, cliquez sur le bouton en regard de Linéaire comme option de ligne de tendance, puis cochez la case en regard de Afficher l’équation sur le graphique :

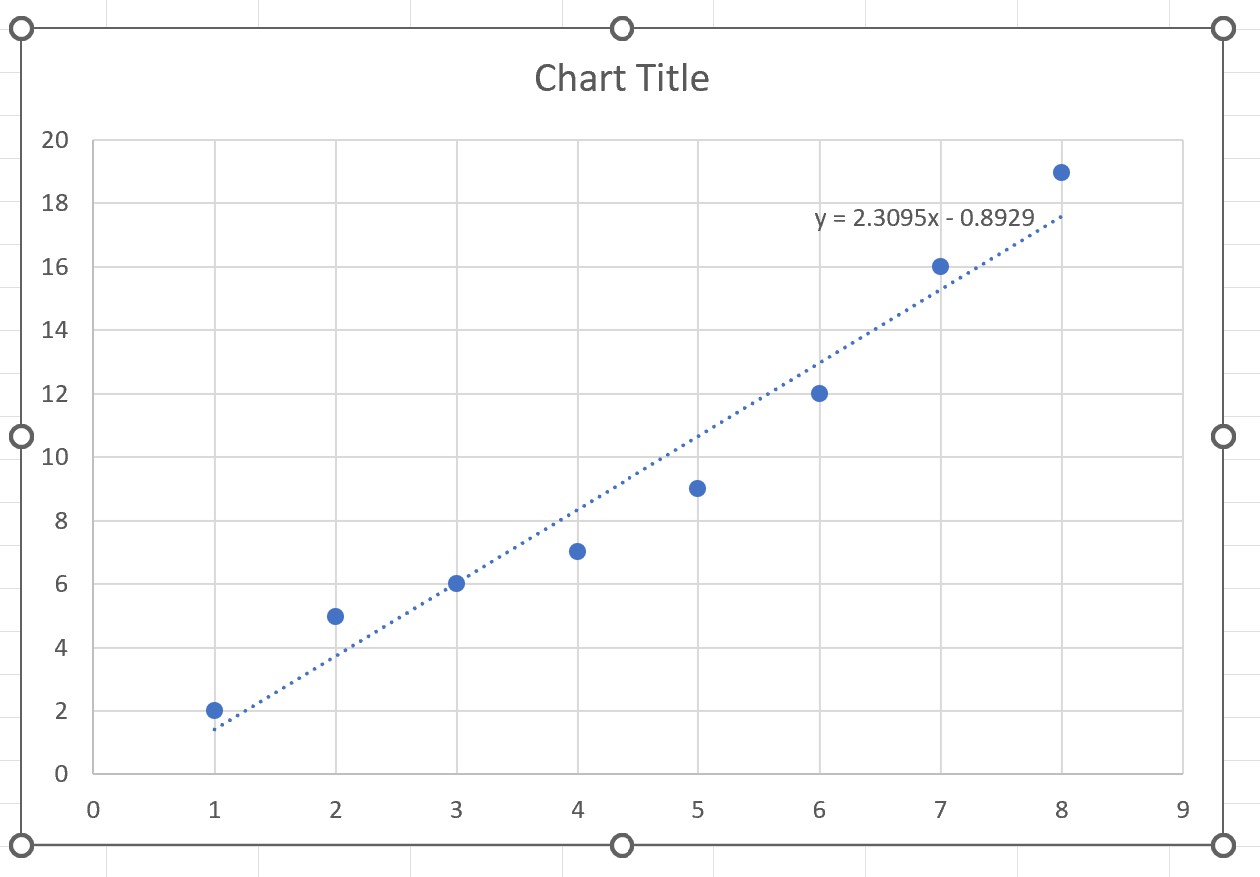
La ligne la mieux ajustée ainsi que l’équation de la ligne apparaîtront sur le graphique :

Étape 4 : Interpréter la ligne de meilleur ajustement

À partir du graphique, nous pouvons voir que la droite de meilleur ajustement a l’équation suivante :

y = 2,3095x – 0,8929

Voici comment interpréter cette équation :

• Pour chaque heure supplémentaire passée à pratiquer, la moyenne des points marqués augmente de 2,3095 .
• Pour un joueur qui pratique zéro heure, la moyenne des points marqués devrait être de -0,8929 .

Notez qu’il n’est pas toujours logique d’interpréter la valeur d’origine dans une équation de régression.

Par exemple, il n’est pas possible pour un joueur de marquer des points négatifs.

Dans cet exemple particulier, nous sommes principalement intéressés par la valeur de la pente de la droite de régression qui est 2,3095 .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans Excel :

Comment effectuer une régression linéaire simple dans Excel
Comment effectuer une régression linéaire multiple dans Excel
Comment calculer R-carré dans Excel