Comment utiliser la méthode Elbow en Python pour trouver des clusters optimaux

L’un des algorithmes de clustering les plus courants dans l’apprentissage automatique est connu sous le nom de clustering k-means .

Le clustering K-means est une technique dans laquelle nous plaçons chaque observation d’un ensemble de données dans l’un des K clusters.

L’objectif final est d’avoir K clusters dans lesquels les observations au sein de chaque cluster sont assez similaires les unes aux autres tandis que les observations dans différents clusters sont assez différentes les unes des autres.

Lors du clustering k-means, la première étape consiste à choisir une valeur pour K – le nombre de clusters dans lesquels nous souhaitons placer les observations.

L’une des façons les plus courantes de choisir une valeur pour K est connue sous le nom de méthode du coude , qui consiste à créer un tracé avec le nombre de clusters sur l’axe des x et le total dans la somme des carrés sur l’axe des y, puis à identifier où un « coude » ou un virage apparaît dans l’intrigue.

Le point sur l’axe des x où se produit le « coude » nous indique le nombre optimal de clusters à utiliser dans l’algorithme de clustering k-means.

L’exemple suivant montre comment utiliser la méthode elbow en Python.

Étape 1 : Importer les modules nécessaires

Tout d’abord, nous importerons tous les modules dont nous aurons besoin pour effectuer le clustering k-means :

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

Étape 2 : Créer le DataFrame

Ensuite, nous allons créer un DataFrame contenant trois variables pour 20 joueurs de basket différents :

#create DataFrame
df = pd.DataFrame({'points': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   'assists': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   'rebounds': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df.dropna()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler().fit_transform(df)

Étape 3 : Utilisez la méthode Elbow pour trouver le nombre optimal de clusters

Supposons que nous souhaitions utiliser le clustering k-means pour regrouper des acteurs similaires sur la base de ces trois métriques.

Pour effectuer un clustering k-means en Python, nous pouvons utiliser la fonction KMeans du module sklearn .

L’argument le plus important de cette fonction est n_clusters , qui spécifie dans combien de clusters placer les observations.

Pour déterminer le nombre optimal de clusters, nous allons créer un graphique qui affiche le nombre de clusters ainsi que le SSE (somme des erreurs quadratiques) du modèle.

On cherchera alors un « coude » où la somme des carrés commence à « se plier » ou à se stabiliser. Ce point représente le nombre optimal de clusters.

Le code suivant montre comment créer ce type de tracé qui affiche le nombre de clusters sur l’axe des x et le SSE sur l’axe des y :

#initialize kmeans parameters
kmeans_kwargs = {
"init": "random",
"n_init": 10,
"random_state": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, **kmeans_kwargs)
    kmeans.fit(scaled_df)
    sse.append(kmeans.inertia_)

#visualize results
plt.plot(range(1, 11), sse)
plt.xticks(range(1, 11))
plt.xlabel("Number of Clusters")
plt.ylabel("SSE")
plt.show()

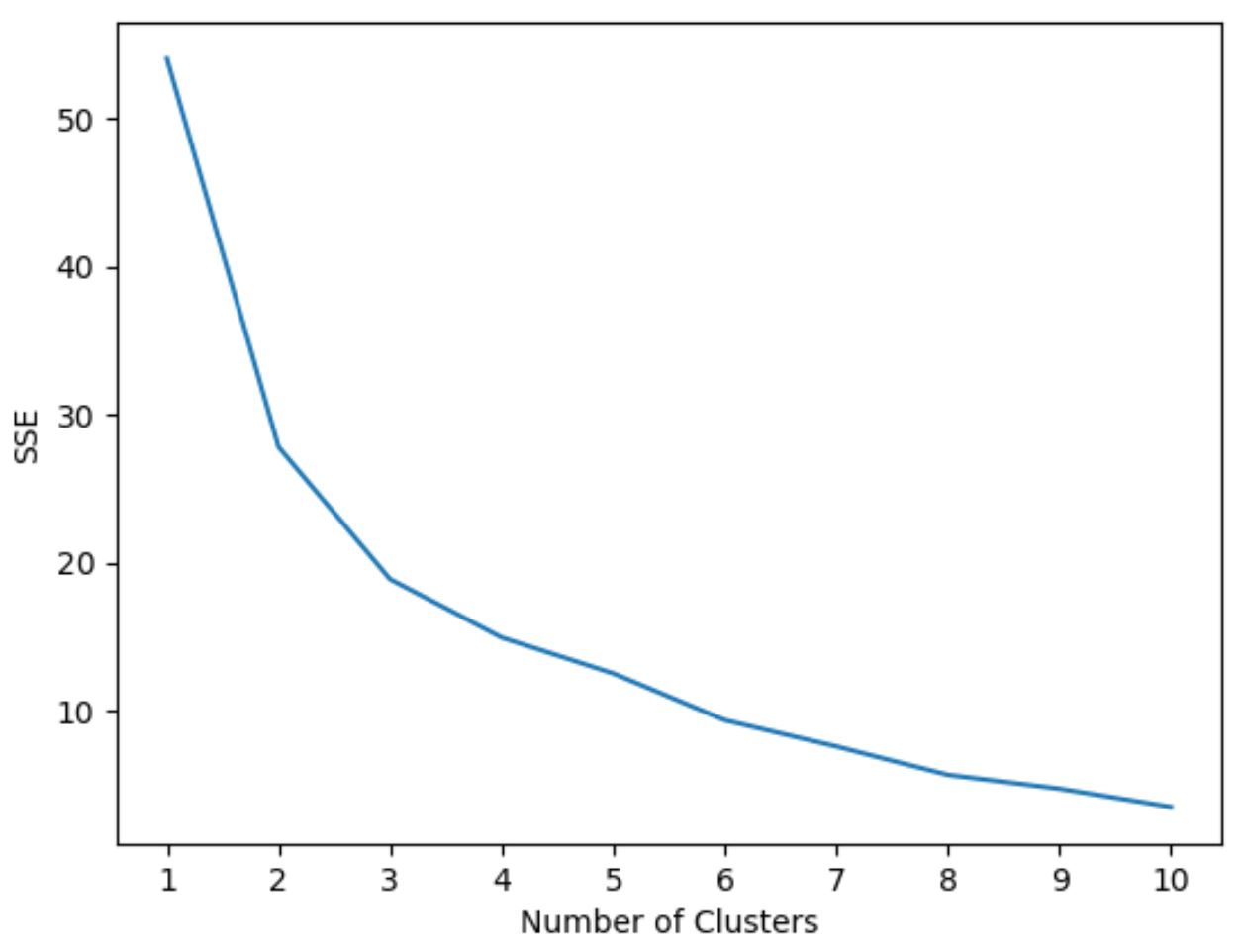
Dans ce graphique, il apparaît qu’il y a un coude ou un « coude » à k = 3 clusters .

Ainsi, nous utiliserons 3 clusters lors de l’ajustement de notre modèle de clustering k-means à l’étape suivante.

Étape 4 : Effectuer un clustering K-Means avec Optimal K

Le code suivant montre comment effectuer un clustering k-means sur l’ensemble de données en utilisant la valeur optimale pour k sur 3 :

#instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init="random", n_clusters=3, n_init=10, random_state=1)

#fit k-means algorithm to data
kmeans.fit(scaled_df)

#view cluster assignments for each observation
kmeans.labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

Le tableau résultant montre les affectations de cluster pour chaque observation dans le DataFrame.

Pour faciliter l’interprétation de ces résultats, nous pouvons ajouter une colonne au DataFrame qui montre l’affectation du cluster de chaque joueur :

#append cluster assingments to original DataFrame
df['cluster'] = kmeans.labels_

#view updated DataFrame
print(df)

    points  assists  rebounds  cluster
0     18.0      3.0        15        1
2     19.0      4.0        14        1
3     14.0      5.0        10        1
4     14.0      4.0         8        1
5     11.0      7.0        14        1
6     20.0      8.0        13        1
7     28.0      7.0         9        2
8     30.0      6.0         5        2
9     31.0      9.0         4        0
10    35.0     12.0        11        0
11    33.0     14.0         6        0
13    25.0      9.0         5        0
14    25.0      4.0         3        2
15    27.0      3.0         8        2
16    29.0      4.0        12        2
17    30.0     12.0         7        0
18    19.0     15.0         6        0
19    23.0     11.0         5        0

La colonne de cluster contient un numéro de cluster (0, 1 ou 2) auquel chaque joueur a été attribué.

Les joueurs appartenant au même cluster ont des valeurs à peu près similaires pour les colonnes de points , de passes décisives et de rebonds .

Remarque : Vous pouvez trouver la documentation complète de la fonction KMeans de sklearn ici .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes en Python :

Comment effectuer une régression linéaire en Python
Comment effectuer une régression logistique en Python
Comment effectuer une validation croisée K-Fold en Python