Comment déterminer si une distribution de probabilité est valide

Une distribution de probabilité nous indique la probabilité qu’une variable aléatoire prenne certaines valeurs.

Pour qu’une distribution de probabilité soit valide, elle doit répondre à deux exigences :

1. Chaque probabilité doit être comprise entre 0 et 1.

2. La somme des probabilités doit totaliser 1.

Si ces deux conditions sont remplies, alors la distribution de probabilité est valide.

Les exemples suivants montrent comment vérifier si différentes distributions de probabilité sont valides.

Exemple 1 : Buts marqués lors d’un match de football

La distribution de probabilité suivante montre la probabilité qu’une certaine équipe de football marque un certain nombre de buts dans un match :

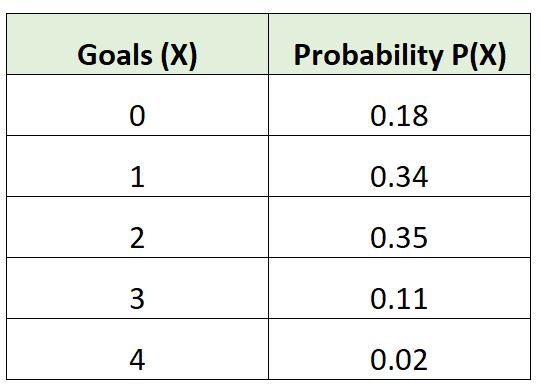
Vérifions si cette distribution de probabilité répond aux deux exigences pour être valide :

1. Chaque probabilité doit être comprise entre 0 et 1.

Nous pouvons voir que chaque probabilité individuelle est comprise entre 0 et 1.

2. La somme des probabilités doit totaliser 1.

Nous pouvons voir que la somme des probabilités totalise 1 :

Somme = 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1

Les deux conditions sont remplies, cette distribution de probabilité est donc valide .

Exemple 2 : ventes réalisées en un mois

La distribution de probabilité suivante montre la probabilité qu’un vendeur donné réalise un certain nombre de ventes au cours du mois à venir :

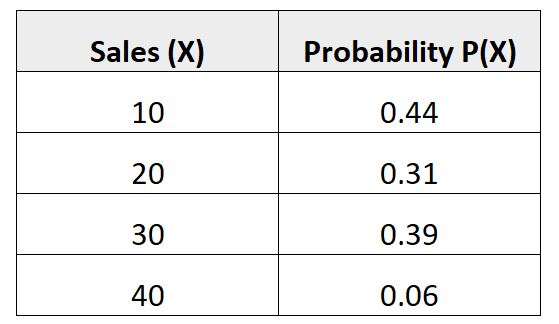
Vérifions si cette distribution de probabilité répond aux deux exigences pour être valide :

1. Chaque probabilité doit être comprise entre 0 et 1.

Nous pouvons voir que chaque probabilité individuelle est comprise entre 0 et 1.

2. La somme des probabilités doit totaliser 1.

On voit que la somme des probabilités ne fait pas 1 :

Somme = 0,44 + 0,31 + 0,39 + 0,06 = 1,2

Les deux conditions ne sont pas remplies et cette distribution de probabilité n’est donc pas valide .

Exemple 3 : Nombre de pannes de batterie

La distribution de probabilité suivante nous indique la probabilité qu’un véhicule donné subisse un certain nombre de pannes de batterie sur une période de 10 ans :

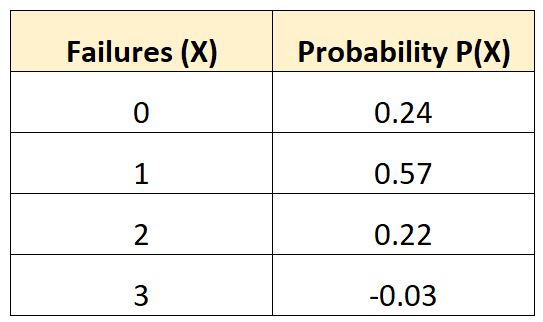
Vérifions si cette distribution de probabilité répond aux deux exigences pour être valide :

1. Chaque probabilité doit être comprise entre 0 et 1.

Nous pouvons voir que chaque probabilité individuelle n’est pas comprise entre 0 et 1.

La dernière probabilité du tableau est une valeur négative.

2. La somme des probabilités doit totaliser 1.

Nous pouvons voir que la somme des probabilités totalise 1 :

Somme = 0,24 + 0,57 + 0,22 – 0,03 = 1

Les deux conditions ne sont pas remplies et cette distribution de probabilité n’est donc pas valide .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les distributions de probabilité :

Comment trouver la moyenne d’une distribution de probabilité
Comment trouver la variance d’une distribution de probabilité
Comment trouver l’écart type d’une distribution de probabilité