Comment calculer Sxy en statistiques (avec exemple)
En statistique, Sxy représente la somme du produit des différences entre les valeurs x et la moyenne de x et les différences entre les valeurs y et la moyenne de y.
Cette valeur est souvent calculée lors de l’ajustement manuel d’un modèle de régression linéaire simple .
Nous utilisons la formule suivante pour calculer Sxy :
Sxy = Σ(x je – x )(y je – y )
où:
- Σ : Un symbole qui signifie « somme »
- x i : La ième valeur de x
- x : La valeur moyenne de x
- y i : La ième valeur de y
- y : La valeur moyenne de y
L’exemple suivant montre comment utiliser cette formule dans la pratique.
Exemple : Calculer Sxy à la main
Supposons que nous souhaitions adapter un modèle de régression linéaire simple à l’ensemble de données suivant :
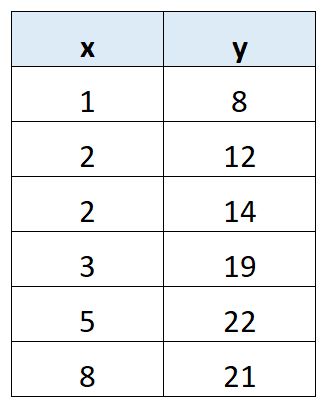
Supposons que nous souhaitions calculer Sxy pour cet ensemble de données.
Tout d’abord, il faut calculer la valeur moyenne de x :
- x = (1 + 2 + 2 + 3 + 5 + 8) / 6 = 3,5
Ensuite, il faut calculer la valeur moyenne de y :
- y = (8 + 12 + 14 + 19 + 22 + 21) / 6 = 16
À l’aide de ces valeurs, la capture d’écran suivante montre comment calculer la valeur de Sxy :
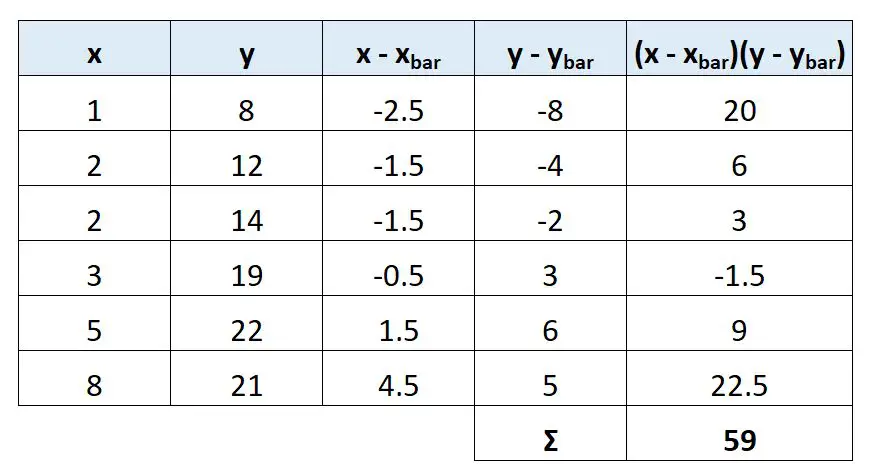
La valeur de Sxy s’avère être 59 .
Notez que nous pourrions également utiliser le calculateur Sxy pour calculer automatiquement la valeur de Sxy pour ce modèle :

La calculatrice renvoie une valeur de 59 , qui correspond à la valeur que nous avons calculée manuellement.
Notez que nous utilisons les formules suivantes pour effectuer manuellement une régression linéaire simple :
y = a + bx
où:
- a = y – bx
- b = Sxy / Sxx
Le calcul pour Sxy n’est qu’un calcul que nous devons effectuer afin d’ajuster un modèle de régression linéaire simple.
Connexes : Comment calculer Sxx dans les statistiques
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans les statistiques :
Comment effectuer une régression linéaire simple à la main
Comment effectuer une régression linéaire multiple à la main
