Comment calculer la valeur attendue de X^2

Pour une variable aléatoire , notée X, vous pouvez utiliser la formule suivante pour calculer la valeur attendue de X ² :

E(X ² ) = Σx ² * p(x)

où:

• Σ : Un symbole qui signifie « somme »
• x : La valeur de la variable aléatoire
• p(x) : La probabilité que la variable aléatoire prenne une valeur donnée

L’exemple suivant montre comment utiliser cette formule dans la pratique.

Exemple : Calcul de la valeur attendue de X ²

Supposons que nous ayons le tableau de distribution de probabilité suivant qui décrit la probabilité qu’une variable aléatoire, X, prenne différentes valeurs :

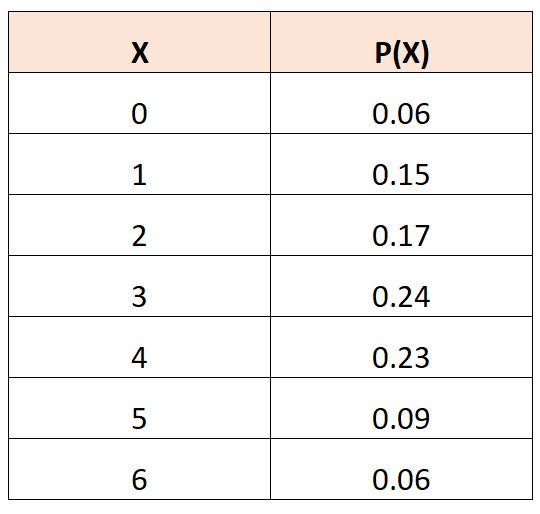
Pour calculer la valeur attendue de X ² , nous pouvons utiliser la formule suivante :

E(X ² ) = Σx ² * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

E(X ² ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16

E( ^X2 ) = 11,08

La valeur attendue de X ² est 11,08 .

Notez que cette variable aléatoire est une variable aléatoire discrète , ce qui signifie qu’elle ne peut prendre qu’un nombre fini de valeurs.

Si X est une variable aléatoire continue , il faut utiliser la formule suivante pour calculer la valeur attendue de X ² :

E(X ² ) = ∫ x ² f(x)dx

où:

• ∫ : Un symbole qui signifie « intégration »
• f(x) : La pdf continue pour la variable aléatoire X

Lors du calcul de la valeur attendue de X ² pour une variable aléatoire continue, nous utilisons généralement un logiciel statistique car ce calcul peut être plus difficile à effectuer manuellement.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans les statistiques :

Comment trouver la moyenne d’une distribution de probabilité
Comment trouver l’écart type d’une distribution de probabilité
Comment trouver la variance d’une distribution de probabilité