Comment calculer les intervalles de confiance dans SAS
Un intervalle de confiance est une plage de valeurs susceptible de contenir un paramètre de population avec un certain niveau de confiance.
Ce tutoriel explique comment calculer les intervalles de confiance suivants dans R :
1. Intervalle de confiance pour une moyenne de population
2. Intervalle de confiance pour une différence dans les moyennes de la population
Allons-y !
Exemple 1 : Intervalle de confiance pour la moyenne de la population dans SAS
Supposons que nous disposions de l’ensemble de données suivant contenant la hauteur (en pouces) d’un échantillon aléatoire de 12 plantes appartenant toutes à la même espèce :
/*create dataset*/ data my_data; input Height; datalines; 14 14 16 13 12 17 15 14 15 13 15 14 ; run; /*view dataset*/ proc print data=my_data;
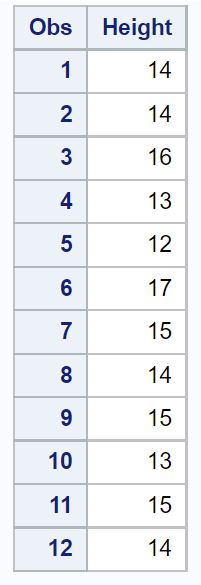
Supposons que nous souhaitions calculer un niveau de confiance de 95 % pour la taille moyenne réelle de la population de cette espèce.
Nous pouvons utiliser le code suivant dans SAS pour ce faire :
/*generate 95% confidence interval for population mean*/ proc ttest data=my_data alpha=0.05; var Height; run;
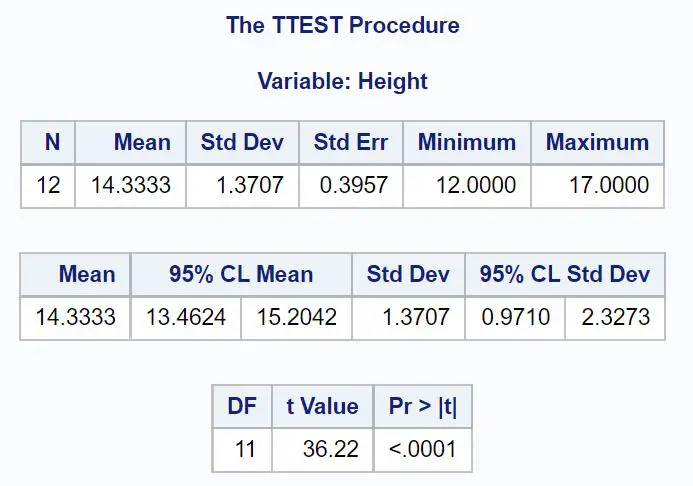
La valeur de Moyenne indique la moyenne de l’échantillon et les valeurs inférieures à 95 % CL Moyenne affichent l’intervalle de confiance à 95 % pour la moyenne de la population.
D’après les résultats, nous pouvons voir que l’intervalle de confiance à 95 % pour le poids moyen des plantes de cette population est de [13,4624 pouces, 15,2042 pouces] .
Exemple 2 : Intervalle de confiance pour la différence des moyennes de population dans SAS
Supposons que nous disposions de l’ensemble de données suivant contenant la hauteur (en pouces) d’un échantillon aléatoire de plantes appartenant à deux espèces différentes :
/*create dataset*/
data my_data2;
input Species $ Height;
datalines;
A 14
A 14
A 16
A 13
A 12
A 17
A 15
A 14
A 15
A 13
B 15
B 14
B 19
B 19
B 17
B 18
B 20
B 19
B 17
B 15
;
run;
/*view dataset*/
proc print data=my_data2;
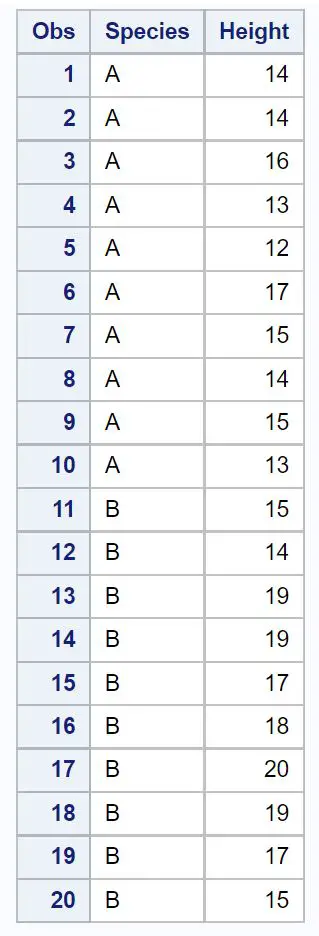
Supposons que nous souhaitions calculer un niveau de confiance de 95 % pour la différence de taille moyenne de la population entre l’espèce A et l’espèce B.
Nous pouvons utiliser le code suivant dans SAS pour ce faire :
/*sort data by Species to ensure confidence interval is calculated correctly*/
proc sort data=my_data2;
by Species;
run;
/*generate 95% confidence interval for difference in population means*/
proc ttest data=my_data2 alpha=0.05;
class Species;
var Height;
run;
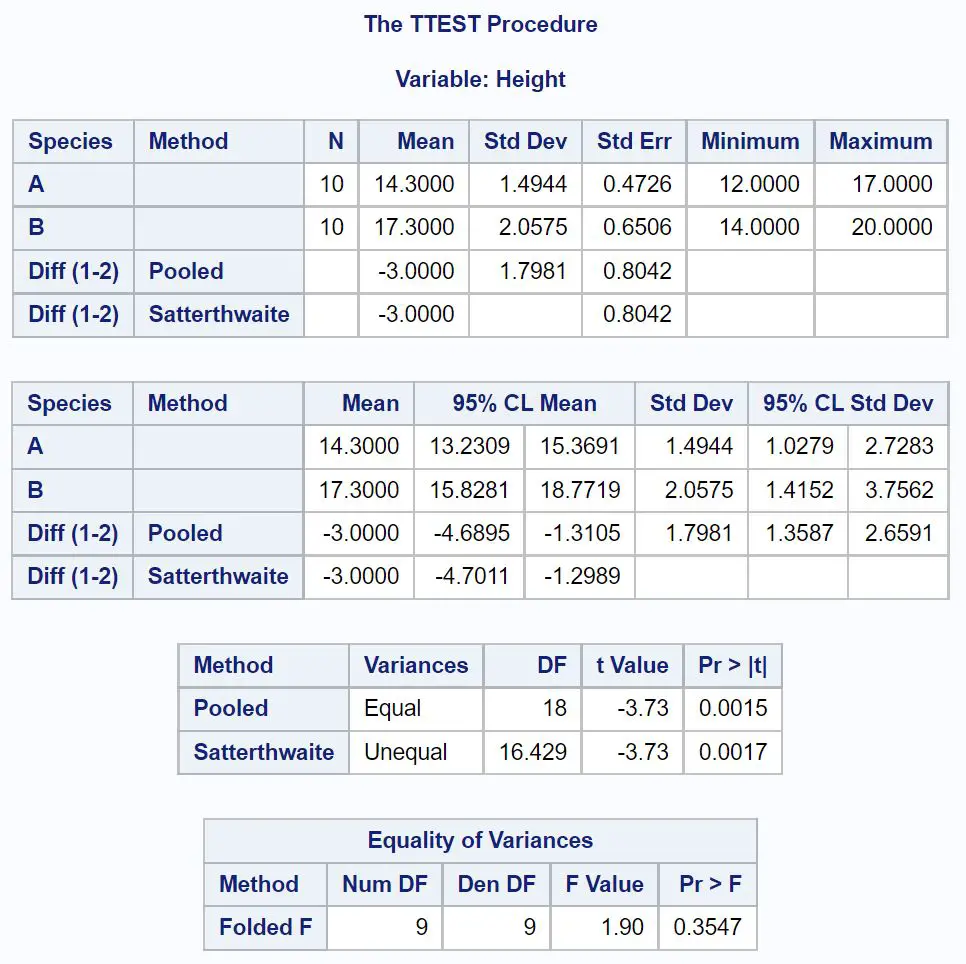
Le premier tableau que nous devons examiner dans le résultat est Equality of Variances , qui teste si la variance entre chaque échantillon est égale ou non.
Puisque la valeur p n’est pas inférieure à 0,05 dans ce tableau, nous pouvons supposer que les écarts entre les deux groupes sont égaux.
Ainsi, nous pouvons examiner la ligne qui utilise la variance groupée pour trouver l’intervalle de confiance à 95 % pour la différence dans les moyennes de la population.
À partir du résultat, nous pouvons voir que l’intervalle de confiance à 95 % pour la différence entre les moyennes de la population est de [-4,6895 pouces, -1,1305 pouces] .
Cela nous indique que nous pouvons être sûrs à 95 % que la véritable différence entre la hauteur moyenne des plantes de l’espèce A et celle de l’espèce B se situe entre -4,6895 pouces et -1,1305 pouces.
Puisque 0 n’est pas dans cet intervalle de confiance , cela indique qu’il existe une différence statistiquement significative entre les moyennes des deux populations.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :
Comment effectuer un test t sur un échantillon dans SAS
Comment effectuer un test t à deux échantillons dans SAS
Comment effectuer un test t pour échantillons appariés dans SAS
