Comment utiliser la méthode des moindres carrés dans R

La méthode des moindres carrés est une méthode que nous pouvons utiliser pour trouver la droite de régression qui correspond le mieux à un ensemble de données donné.

Pour utiliser la méthode des moindres carrés pour ajuster une droite de régression dans R, on peut utiliser la fonction lm() .

Cette fonction utilise la syntaxe de base suivante :

model <- lm(response ~ predictor, data=df)

L’exemple suivant montre comment utiliser cette fonction dans R.

Exemple : méthode des moindres carrés dans R

Supposons que nous ayons le bloc de données suivant dans R qui montre le nombre d’heures étudiées et la note d’examen correspondante pour 15 étudiants dans une classe :

#create data frame
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1     1    64
2     2    66
3     4    76
4     5    73
5     5    74
6     6    81

Nous pouvons utiliser la fonction lm() pour utiliser la méthode des moindres carrés pour ajuster une droite de régression à ces données :

#use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min     1Q Median     3Q    Max 
-5.140 -3.219 -1.193  2.816  5.772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   65.334      2.106  31.023 1.41e-13 ***
hours          1.982      0.248   7.995 2.25e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared:  0.831,	Adjusted R-squared:  0.818 
F-statistic: 63.91 on 1 and 13 DF,  p-value: 2.253e-06

À partir des valeurs de la colonne Estimation du résultat, nous pouvons écrire la droite de régression ajustée suivante :

Score d’examen = 65,334 + 1,982 (heures)

Voici comment interpréter chaque coefficient du modèle :

• Interception : Pour un étudiant qui étudie 0 heure, la note attendue à l’examen est de 65,334 .
• heures : Pour chaque heure supplémentaire étudiée, la note attendue à l’examen augmente de 1,982 .

Nous pouvons utiliser cette équation pour estimer la note à l’examen qu’un étudiant recevra en fonction de ses heures étudiées.

Par exemple, si un étudiant étudie pendant 5 heures, nous estimerions que sa note à l’examen serait de 75,244 :

Score d’examen = 65,334 + 1,982(5) = 75,244

Enfin, nous pouvons créer un nuage de points des données originales avec la droite de régression ajustée superposée sur le tracé :

#create scatter plot of data
plot(df$hours, df$score, pch=16, col='steelblue')

#add fitted regression line to scatter plot
abline(model)

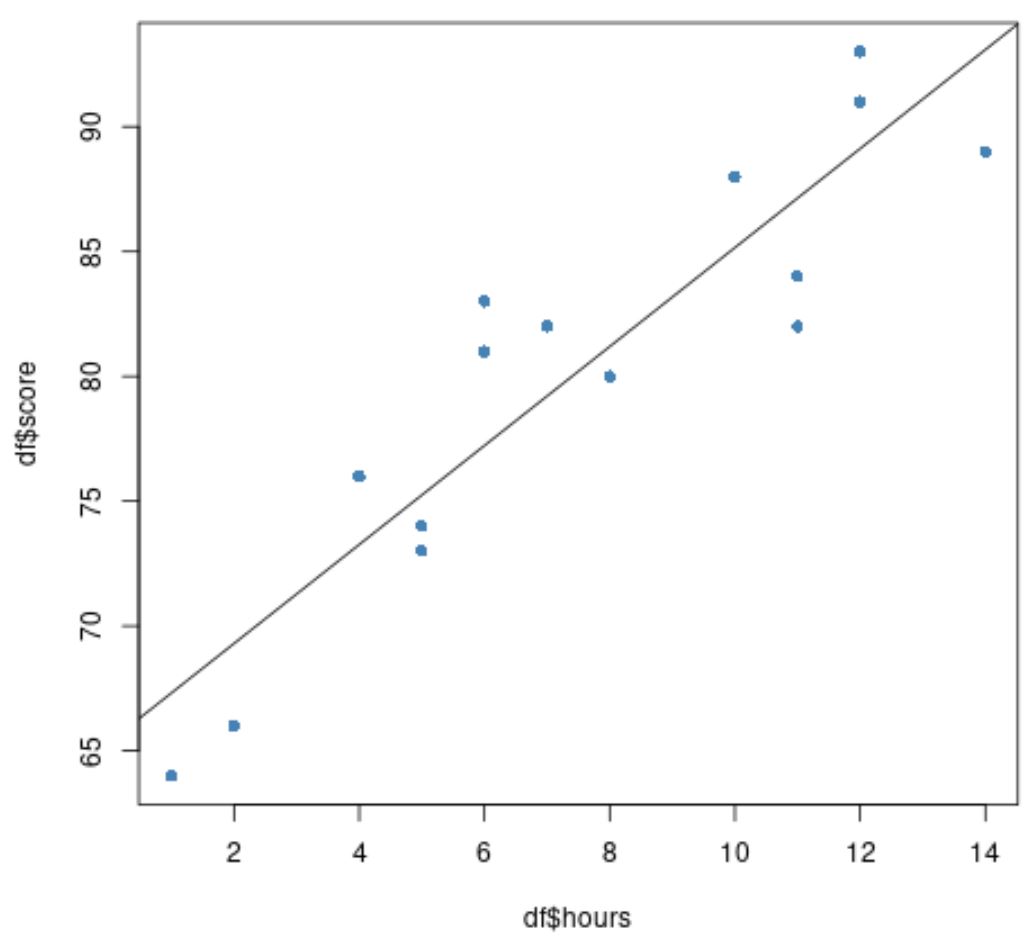
Les cercles bleus représentent les données et la ligne noire représente la droite de régression ajustée.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment créer un tracé résiduel dans R
Comment tester la multicolinéarité dans R
Comment effectuer un ajustement de courbe dans R