Comment trouver la probabilité d’au moins une tête dans les lancers de pièces

Pour un tirage au sort donné, la probabilité d’obtenir « face » est de 1/2 ou 0,5.

Pour trouver la probabilité d’avoir au moins une face lors d’un certain nombre de lancers de pièces, vous pouvez utiliser la formule suivante :

P(Au moins une tête) = 1 – 0,5 ⁿ

où:

• n : Nombre total de retournements

Par exemple, supposons que nous lancions une pièce de monnaie 2 fois.

La probabilité d’obtenir au moins une face lors de ces 3 lancers est :

• P(Au moins une tête) = 1 – 0,5 ⁿ
• P(Au moins une tête) = 1 – 0,5 ³
• P (Au moins une tête) = 1 – 0,125
• P(Au moins une tête) = 0,875

Cette réponse a du sens si nous énumérons tous les résultats possibles pour 2 tirages à pile ou face, avec « T » représentant pile et « H » représentant face :

• TTT
• TTH
• THH
• THT
• HHHH
• VRD
• HTH
• HTT

Notez qu’au moins une tête (H) apparaît dans 7 résultats possibles sur 8, ce qui équivaut à 7/8 = 0,875 .

Ou supposons que nous lancions une pièce de monnaie 5 fois.

La probabilité d’obtenir au moins une face lors de ces 5 lancers est :

• P(Au moins une tête) = 1 – 0,5 ⁿ
• P(Au moins une tête) = 1 – 0,5 ⁵
• P(Au moins une tête) = 1 – 0,25
• P(Au moins une tête) = 0,96875

Le tableau suivant montre la probabilité d’obtenir au moins une face lors de différents nombres de lancers de pièces :

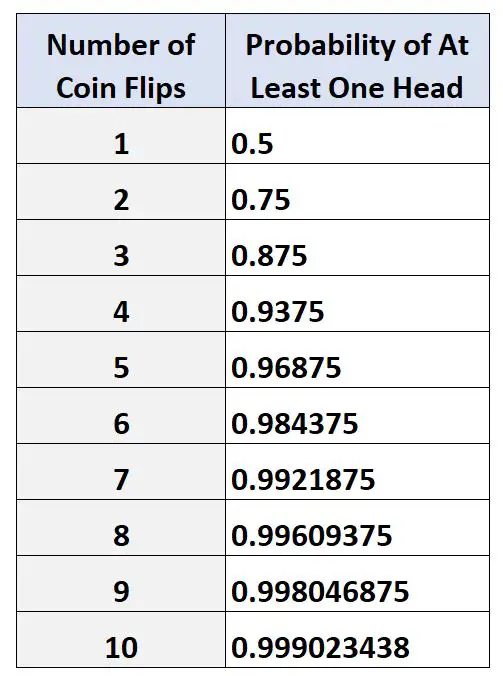
Notez que plus le nombre de lancers de pièces est élevé, plus la probabilité d’obtenir au moins une face est élevée.

Cela devrait avoir du sens compte tenu du fait que nous devrions avoir une probabilité plus élevée de voir éventuellement une tête apparaître si nous continuons à lancer la pièce plusieurs fois.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres calculs courants liés aux probabilités :

Comment trouver la probabilité de « au moins un » succès
Comment trouver la probabilité d’« au moins deux » succès
Comment trouver la probabilité de A et B
Comment trouver la probabilité de A ou B