Comment utiliser la méthode Elbow dans R pour trouver des clusters optimaux
L’un des algorithmes de clustering les plus couramment utilisés dans l’apprentissage automatique est connu sous le nom de clustering k-means .
Le clustering K-means est une technique dans laquelle nous plaçons chaque observation d’un ensemble de données dans l’un des K clusters.
L’objectif final est d’avoir K clusters dans lesquels les observations au sein de chaque cluster sont assez similaires les unes aux autres tandis que les observations dans différents clusters sont assez différentes les unes des autres.
Lors du clustering k-means, la première étape consiste à choisir une valeur pour K – le nombre de clusters dans lesquels nous souhaitons placer les observations.
L’une des façons les plus courantes de choisir une valeur pour K est connue sous le nom de méthode du coude , qui consiste à créer un tracé avec le nombre de clusters sur l’axe des x et le total dans la somme des carrés sur l’axe des y, puis à identifier où un « coude » ou un virage apparaît dans l’intrigue.
Le point sur l’axe des x où se produit le « coude » nous indique le nombre optimal de clusters à utiliser dans l’algorithme de clustering k-means.
L’exemple suivant montre comment utiliser la méthode du coude dans R.
Exemple : utilisation de la méthode Elbow dans R
Pour cet exemple, nous utiliserons l’ensemble de données USArrests intégré à R, qui contient le nombre d’arrestations pour 100 000 habitants dans chaque État américain en 1973 pour meurtre, agression et viol, ainsi que le pourcentage de la population de chaque État vivant dans des zones urbaines. , UrbanPop.
Le code suivant montre comment charger l’ensemble de données, supprimer les lignes avec des valeurs manquantes et mettre à l’échelle chaque variable de l’ensemble de données pour avoir une moyenne de 0 et un écart type de 1 :
#load data df <- USArrests #remove rows with missing values df <- na.omit(df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
Pour trouver le nombre optimal de clusters à utiliser dans l’algorithme k-means, nous utiliserons la fonction fviz_nbclust() du package factoextra pour créer un tracé du nombre de clusters par rapport au total dans la somme des carrés :
library(cluster) library(factoextra) #create plot of number of clusters vs total within sum of squares fviz_nbclust(df, kmeans, method = "wss")
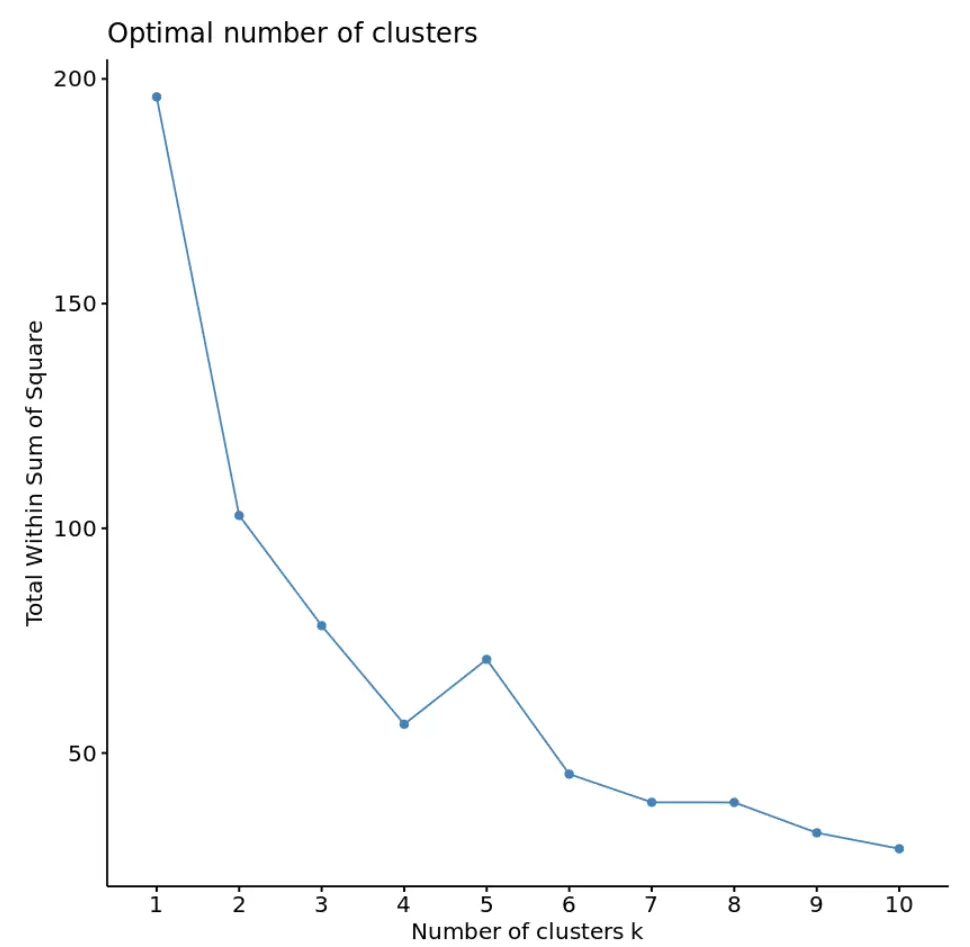
Dans ce graphique, il apparaît qu’il y a un « coude » ou un coude à k = 4 clusters. C’est le point où le total dans la somme des carrés commence à se stabiliser.
Cela nous indique que le nombre optimal de clusters à utiliser dans l’algorithme des k-moyennes est de 4.
Remarque : Bien que nous puissions obtenir un total inférieur dans la somme des carrés en utilisant plus de clusters, nous surajusterions probablement les données d’entraînement et donc l’algorithme des k-moyennes ne fonctionnerait pas aussi bien sur les données de test.
Nous pouvons utiliser la fonction kmeans() du package cluster pour effectuer un clustering k-means sur l’ensemble de données en utilisant la valeur optimale pour k de 4 :
#make this example reproducible set.seed(1) #perform k-means clustering with k = 4 clusters km <- kmeans(df, centers = 4, nstart = 25) #view results km K-means clustering with 4 clusters of sizes 16, 13, 13, 8 Cluster means: Murder Assault UrbanPop Rape 1 -0.4894375 -0.3826001 0.5758298 -0.26165379 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 0.6950701 1.0394414 0.7226370 1.27693964 4 1.4118898 0.8743346 -0.8145211 0.01927104 Clustering vector: Alabama Alaska Arizona Arkansas California Colorado 4 3 3 4 3 3 Connecticut Delaware Florida Georgia Hawaii Idaho 1 1 3 4 1 2 Illinois Indiana Iowa Kansas Kentucky Louisiana 3 1 2 1 2 4 Maine Maryland Massachusetts Michigan Minnesota Mississippi 2 3 1 3 2 4 Missouri Montana Nebraska Nevada New Hampshire New Jersey 3 2 2 3 2 1 New Mexico New York North Carolina North Dakota Ohio Oklahoma 3 3 4 2 1 1 Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 1 1 1 4 2 4 Texas Utah Vermont Virginia Washington West Virginia 3 1 2 1 1 2 Wisconsin Wyoming 2 1 Within cluster sum of squares by cluster: [1] 16.212213 11.952463 19.922437 8.316061 (between_SS / total_SS = 71.2 %) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" [7] "size" "iter" "ifault"
D’après les résultats, nous pouvons voir que :
- 16 États ont été affectés au premier cluster
- 13 États ont été affectés au deuxième cluster
- 13 États ont été affectés au troisième cluster
- 8 États ont été affectés au quatrième cluster
Nous pouvons également ajouter les affectations de cluster de chaque état à l’ensemble de données d’origine :
#add cluster assigment to original data
final_data <- cbind(USArrests, cluster = km$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
Chaque observation de la base de données originale a été placée dans l’un des quatre groupes.
Ressources additionnelles
Les didacticiels suivants fournissent des exemples étape par étape sur la manière d’exécuter divers algorithmes de clustering dans R :
Clustering K-Means dans R : exemple étape par étape
Clustering K-Medoids dans R : exemple étape par étape
Clustering hiérarchique dans R : exemple étape par étape
