Comment comparer des histogrammes (avec des exemples)
Un histogramme est un type de graphique qui nous permet de visualiser la distribution des valeurs dans un ensemble de données.
L’axe des X affiche les valeurs de l’ensemble de données et l’axe des Y montre la fréquence de chaque valeur.
Les histogrammes sont utiles car ils nous permettent de comprendre rapidement la distribution des valeurs dans un ensemble de données. Ils sont également utiles pour comparer deux ensembles de données différents.
Lorsque l’on compare deux histogrammes ou plus, nous pouvons répondre à trois questions différentes :
1. Comment les valeurs médianes se comparent-elles ?
Nous pouvons estimer approximativement que la médiane se situe près du milieu de chaque histogramme, ce qui nous permet de comparer les valeurs médianes des distributions.
2. Comment se compare la dispersion ?
Nous pouvons voir visuellement quel histogramme est le plus étalé, ce qui nous donne une idée de quelle distribution a des valeurs les plus dispersées.
3. Comment l’asymétrie se compare-t-elle ?
Si un histogramme a une « queue » sur le côté gauche du tracé, on dit qu’il est asymétrique négativement. À l’inverse, si un histogramme a une « queue » sur le côté droit du tracé, on dit qu’il est positivement asymétrique. Nous pouvons vérifier visuellement chaque histogramme pour comparer l’ asymétrie .
L’exemple suivant montre comment comparer deux histogrammes différents et répondre à ces trois questions.
Exemple : comparaison d’histogrammes
Supposons que 200 étudiants utilisent une méthode d’étude pour se préparer à un examen et que 200 autres étudiants utilisent une méthode d’étude différente pour se préparer au même examen.
Supposons que nous créions les histogrammes suivants pour comparer les résultats des examens de chaque groupe d’étudiants :
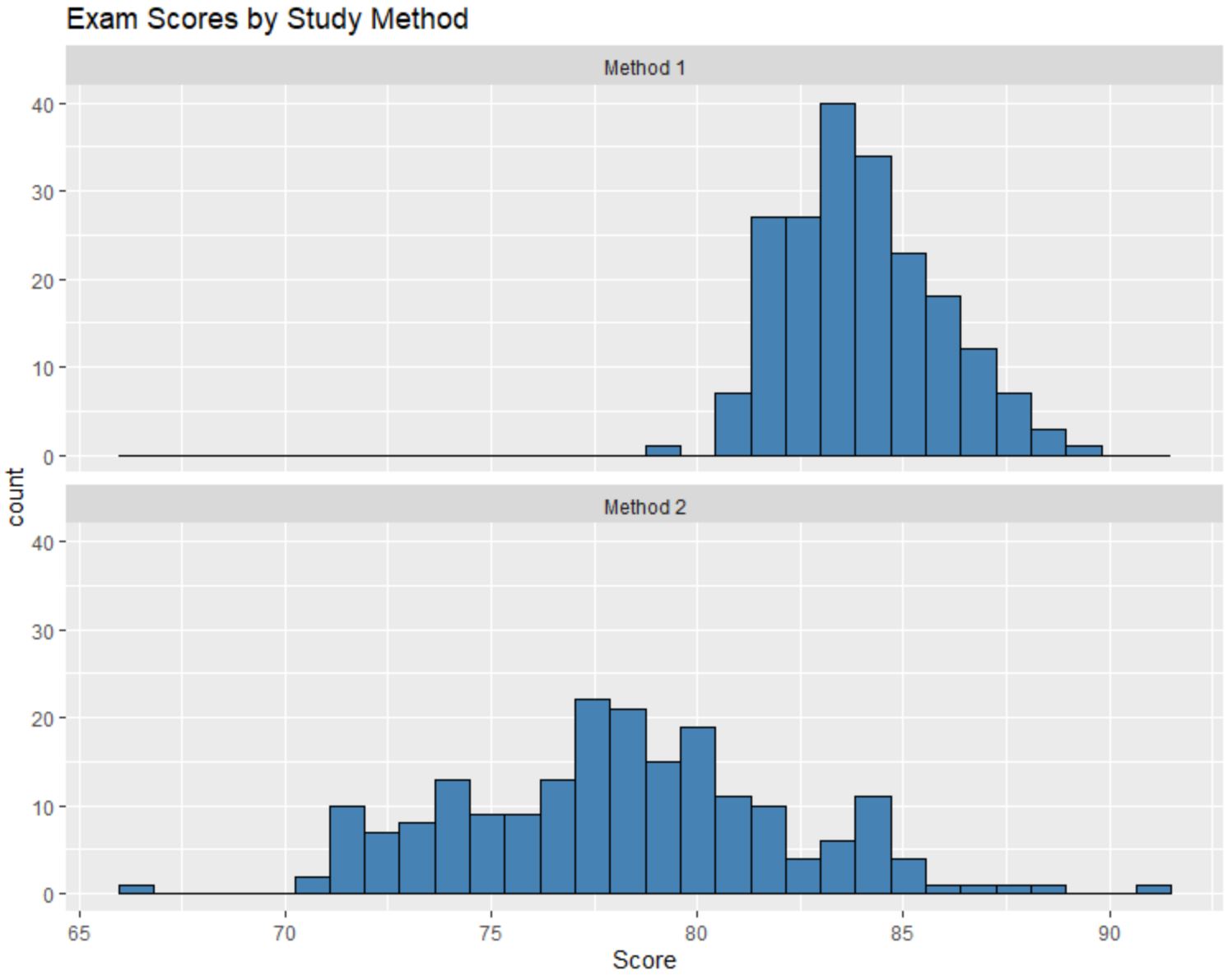
Nous pouvons comparer ces histogrammes et répondre aux trois questions suivantes :
1. Comment les valeurs médianes se comparent-elles ?
Bien que nous ne connaissions pas les valeurs médianes exactes de chaque distribution simplement en regardant les histogrammes, il est évident que la note médiane à l’examen des étudiants ayant utilisé la méthode 1 est supérieure à la note médiane à l’examen des étudiants ayant utilisé la méthode 2.
Nous pourrions estimer que la valeur médiane pour la méthode 1 est d’environ 84 et que la valeur médiane pour la méthode 2 est d’environ 78.
2. Comment se compare la dispersion ?
Les valeurs de l’histogramme de la méthode 2 sont beaucoup plus dispersées que celles de la méthode 1, ce qui nous indique qu’il existe une bien plus grande dispersion dans les résultats des examens pour les étudiants qui ont utilisé la méthode 2.
3. Comment l’asymétrie se compare-t-elle ?
En examinant les histogrammes, il apparaît que la distribution des résultats des examens pour la méthode 1 est légèrement asymétrique vers la droite, comme l’indique la « queue » qui s’étend à droite de l’histogramme.
Il ne semble cependant pas y avoir de « queue » dans la distribution des résultats des examens pour la méthode 2, ce qui nous indique que la distribution est peu ou pas asymétrique.
Bonus : Voici le code que nous avons utilisé dans R pour créer ces deux histogrammes :
library(ggplot2)
#make this example reproducible
set.seed(0)
#create data frame
df <- data.frame(method=rep(c('Method 1', 'Method 2'), each=200),
Score=c(rnorm(200, mean=84, sd=2),
rnorm(200, mean=78, sd=4)))
#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
geom_histogram(fill='steelblue', color='black') +
facet_wrap(.~method, nrow=2) +
labs(title='Exam Scores by Study Method')
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes avec des histogrammes :
Comment estimer la moyenne et la médiane de n’importe quel histogramme
Comment estimer l’écart type de n’importe quel histogramme
Comment décrire la forme des histogrammes
