Comment lire une boîte à moustaches avec des valeurs aberrantes (avec exemple)
Une boîte à moustaches est un type de tracé qui affiche le résumé à cinq chiffres d’un ensemble de données, qui comprend :
- La valeur minimale
- Le premier quartile (le 25e percentile)
- La valeur médiane
- Le troisième quartile (le 75e percentile)
- La valeur maximale
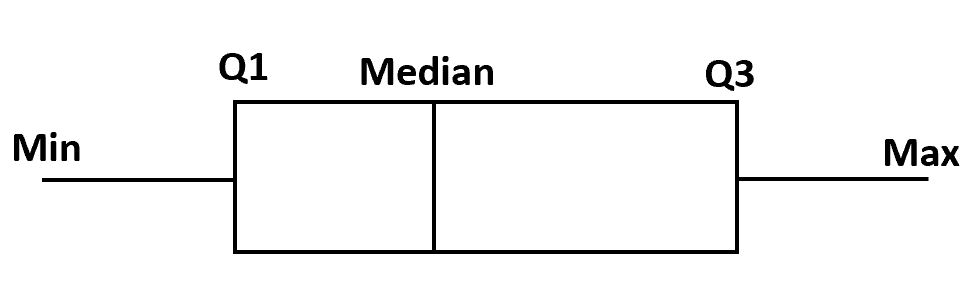
Pour réaliser un box plot, nous dessinons d’abord une boîte du premier au troisième quartile.
Ensuite, nous traçons une ligne verticale au niveau de la médiane.
Enfin, nous dessinons des « moustaches » des quartiles jusqu’à la valeur minimale et maximale.
Dans la plupart des logiciels statistiques, une observation est définie comme une valeur aberrante si elle répond à l’une des deux exigences suivantes :
- L’observation est 1,5 fois l’écart interquartile inférieur au premier quartile (Q1)
- L’observation est 1,5 fois l’écart interquartile supérieur au troisième quartile (Q3).
Si une valeur aberrante existe dans un ensemble de données, elle est généralement étiquetée par un petit point en dehors de la plage des moustaches dans le diagramme en boîte :

Lorsque cela se produit, les valeurs « minimales » et « maximales » dans la boîte à moustaches se voient simplement attribuer les valeurs de Q1 – 1,5*IQR et Q3 + 1,5*IQR, respectivement.
L’exemple suivant montre comment interpréter les diagrammes en boîte avec et sans valeurs aberrantes.
Exemple : Interprétation d’un diagramme en boîte avec des valeurs aberrantes
Supposons que nous créions les deux diagrammes en boîte suivants pour visualiser la répartition des points marqués par les basketteurs de deux équipes différentes :
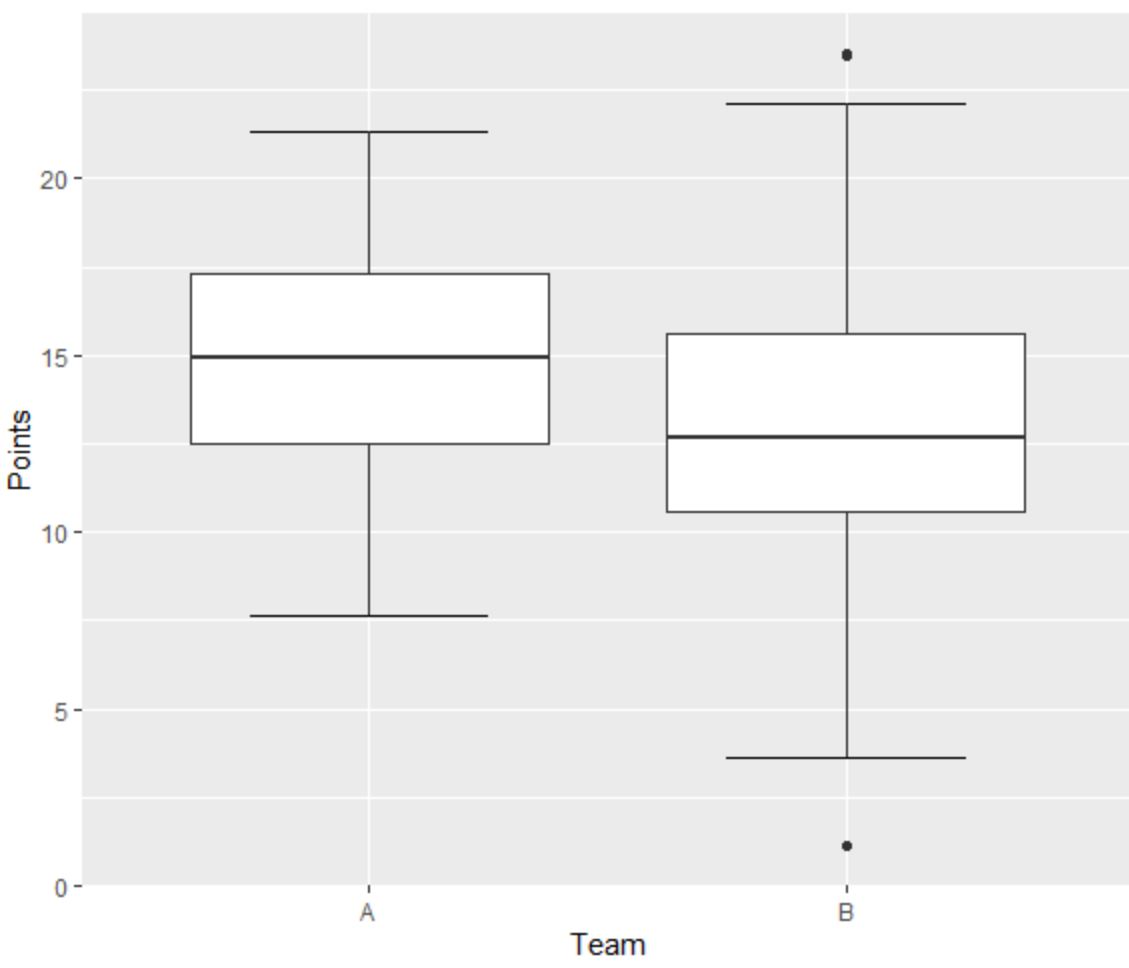
La boîte à moustaches de gauche pour l’équipe A n’a pas de valeurs aberrantes puisqu’il n’y a pas de petits points situés en dehors de la moustache minimale ou maximale.
Cependant, la boîte à moustaches de droite pour l’équipe B présente une valeur aberrante située au-dessus de la valeur « maximale » et une valeur aberrante située en dessous de la valeur « minimale ».
Voici le résumé actuel de cinq chiffres pour la répartition de la variable « Points » pour l’équipe B :
- Valeur minimale : 1,1
- Premier quartile : 10,5
- Médiane : 12,7
- Troisième quartile : 15,6
- Valeur maximale : 23,5
Voici comment calculer les limites des valeurs aberrantes potentielles :
Échelle interquartile : Troisième quartile – Premier quartile = 15,6 – 10,5 = 5,1
Limite inférieure : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85
Limite supérieure : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25
Les moustaches pour les valeurs minimales et maximales dans la boîte à moustaches sont placées à 2,85 et 23,25 .
Ainsi, les observations avec des valeurs de 1,1 et 23,5 sont toutes deux qualifiées de valeurs aberrantes dans le diagramme en boîte car elles se situent en dehors des limites inférieure et supérieure.
Bonus : Voici le code exact que nous avons utilisé pour créer ces deux boîtes à moustaches dans le langage de programmation R :
library(ggplot2) #make this example reproducible set.seed(2) #create data frame df <- data.frame(Team = factor(rep(c("A", "B"), each = 200)), Points = c(rnorm(200, mean = 15, sd = 3), rnorm(200, mean = 12, sd = 4))) #create box plots ggplot(df, aes(x = Team, y = Points)) + stat_boxplot(geom = "errorbar", width = 0.5) + geom_boxplot() #calculate summary statistics for each team tapply(df$Points, df$Team, summary)
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur les diagrammes en boîte :
Comment comparer les boîtes à moustaches
Comment identifier l’asymétrie dans les boîtes à moustaches
Comment trouver l’intervalle interquartile d’une boîte à moustaches
