Un guide complet : le plan factoriel 2×4

Un plan factoriel 2 × 4 est un type de plan expérimental qui permet aux chercheurs de comprendre les effets de deux variables indépendantes sur une seule variable dépendante.

Dans ce type de plan, une variable indépendante comporte deux niveaux et l’autre variable indépendante comporte quatre niveaux.

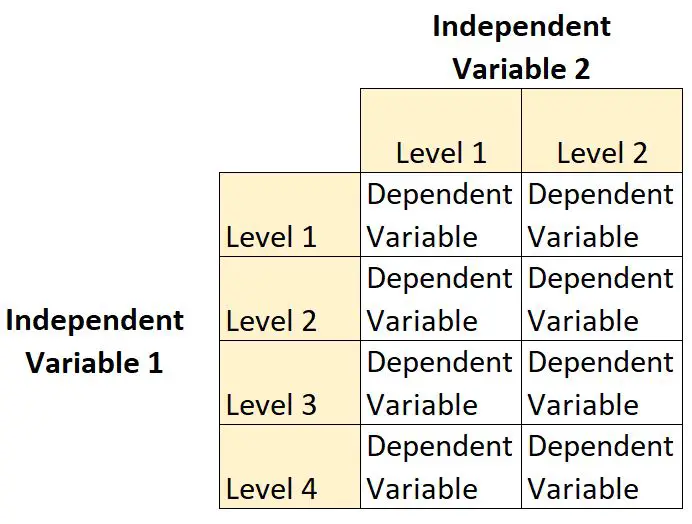
Par exemple, supposons qu’un botaniste souhaite comprendre les effets de la lumière du soleil (aucune, faible, moyenne ou élevée) et de la fréquence d’arrosage (quotidienne ou hebdomadaire) sur la croissance d’une certaine espèce de plante.

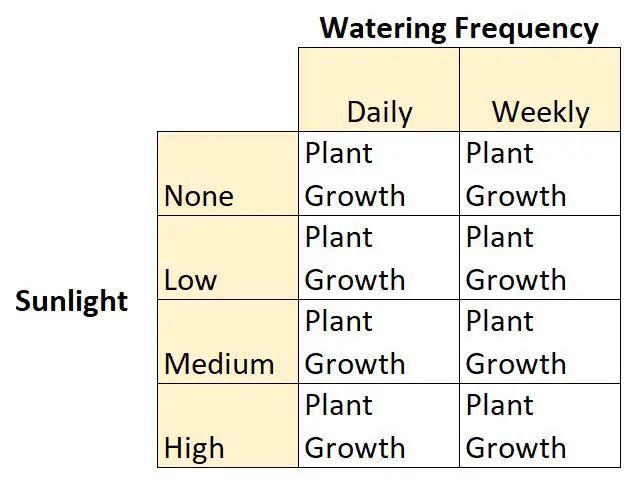
Il s’agit d’un exemple de plan factoriel 2 × 4 car il existe deux variables indépendantes, l’une à deux niveaux et l’autre à quatre niveaux :

• Variable indépendante n°1 : Lumière du soleil
  • Niveaux : Aucun, Faible, Moyen, Élevé
• Variable indépendante n°2 : Fréquence d’arrosage
  • Niveaux : quotidien, hebdomadaire

Et il existe une variable dépendante : la croissance des plantes.

Le but d’un plan factoriel 2 × 4

Un plan factoriel 2×4 permet d’analyser les effets suivants :

Effets principaux : ce sont les effets qu’une seule variable indépendante a sur la variable dépendante.

Par exemple, dans notre scénario précédent, nous pourrions analyser les principaux effets suivants :

• Principal effet du soleil sur la croissance des plantes.
  • Croissance moyenne de toutes les plantes n’ayant reçu aucune lumière solaire.
  • Croissance moyenne de toutes les plantes ayant reçu un faible ensoleillement.
  • Croissance moyenne de toutes les plantes ayant reçu un ensoleillement moyen.
  • Croissance moyenne de toutes les plantes ayant reçu un ensoleillement élevé.
• Effet principal de la fréquence d’arrosage sur la croissance des plantes.
  • Croissance moyenne de toutes les plantes arrosées quotidiennement.
  • Croissance moyenne de toutes les plantes arrosées chaque semaine.

Effets d’interaction : ils se produisent lorsque l’effet d’une variable indépendante sur la variable dépendante dépend du niveau de l’autre variable indépendante.

Par exemple, dans notre scénario précédent, nous pourrions analyser les effets d’interaction suivants :

• L’effet du soleil sur la croissance des plantes dépend-il de la fréquence des arrosages ?
• L’effet de la fréquence d’arrosage sur la croissance des plantes dépend-il de l’ensoleillement ?

Comment analyser un plan factoriel 2 × 4

Nous pouvons effectuer une ANOVA bidirectionnelle pour tester formellement si les variables indépendantes ont ou non une relation statistiquement significative avec la variable dépendante.

Par exemple, le code suivant montre comment effectuer une ANOVA bidirectionnelle pour notre scénario d’usine hypothétique dans R :

#make this example reproducible
set.seed(0)

#create data
df <- data.frame(sunlight = rep(c('None', 'Low', 'Medium', 'High'), each=10, times=2),
                 water = rep(c('Daily', 'Weekly'), each=40, times=2),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value   Pr(>F)    
sunlight         3  744.1  248.04   34.16  < 2e-16 ***
water            1   43.1   43.05    5.93    0.016 *  
sunlight:water   3  195.8   65.27    8.99 1.61e-05 ***
Residuals      152 1103.5    7.26                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Voici comment interpréter le résultat de l’ANOVA :

Effet principal n°1 (lumière du soleil) : La valeur p associée à la lumière du soleil est <2e-16 . Comme ce chiffre est inférieur à 0,05, cela signifie que l’exposition au soleil a un effet statistiquement significatif sur la croissance des plantes.

Effet principal n°2 (Eau) : La valeur p associée à l’eau est de 0,016 . Comme ce chiffre est inférieur à 0,05, cela signifie que la fréquence d’arrosage a également un effet statistiquement significatif sur la croissance des plantes.

Effet d’interaction : La valeur p pour l’interaction entre la lumière du soleil et l’eau est de 0,000061 . Puisque cette valeur est inférieure à 0,05, cela signifie qu’il existe un effet d’interaction entre la lumière du soleil et l’eau.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la conception et l’analyse expérimentales :

Un guide complet : le plan factoriel 2 × 2
Un guide complet : le plan factoriel 2 × 3
Qu’est-ce qu’une ANOVA Factorielle ?