Comment effectuer une régression LOESS dans R (avec exemple)
La régression LOESS , parfois appelée régression locale, est une méthode qui utilise l’ajustement local pour ajuster un modèle de régression à un ensemble de données.
L’exemple étape par étape suivant montre comment effectuer une régression LOESS dans R.
Étape 1 : Créer les données
Tout d’abord, créons le bloc de données suivant dans R :
#view DataFrame df <- data.frame(x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14), y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27)) #view first six rows of data frame head(df) x y 1 1 1 2 2 4 3 3 7 4 4 13 5 5 19 6 6 24
Étape 2 : Ajuster plusieurs modèles de régression LOESS
Nous pouvons utiliser la fonction loess() pour ajuster plusieurs modèles de régression LOESS à cet ensemble de données, en utilisant différentes valeurs pour le paramètre span :
#fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span=.5)
smooth50 <- predict(loess50)
loess75 <- loess(y ~ x, data=df, span=.75)
smooth75 <- predict(loess75)
loess90 <- loess(y ~ x, data=df, span=.9)
smooth90 <- predict(loess90)
#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch=19, main='Loess Regression Models')
lines(smooth50, x=df$x, col='red')
lines(smooth75, x=df$x, col='purple')
lines(smooth90, x=df$x, col='blue')
legend('bottomright', legend=c('.5', '.75', '.9'),
col=c('red', 'purple', 'blue'), pch=19, title='Smoothing Span')
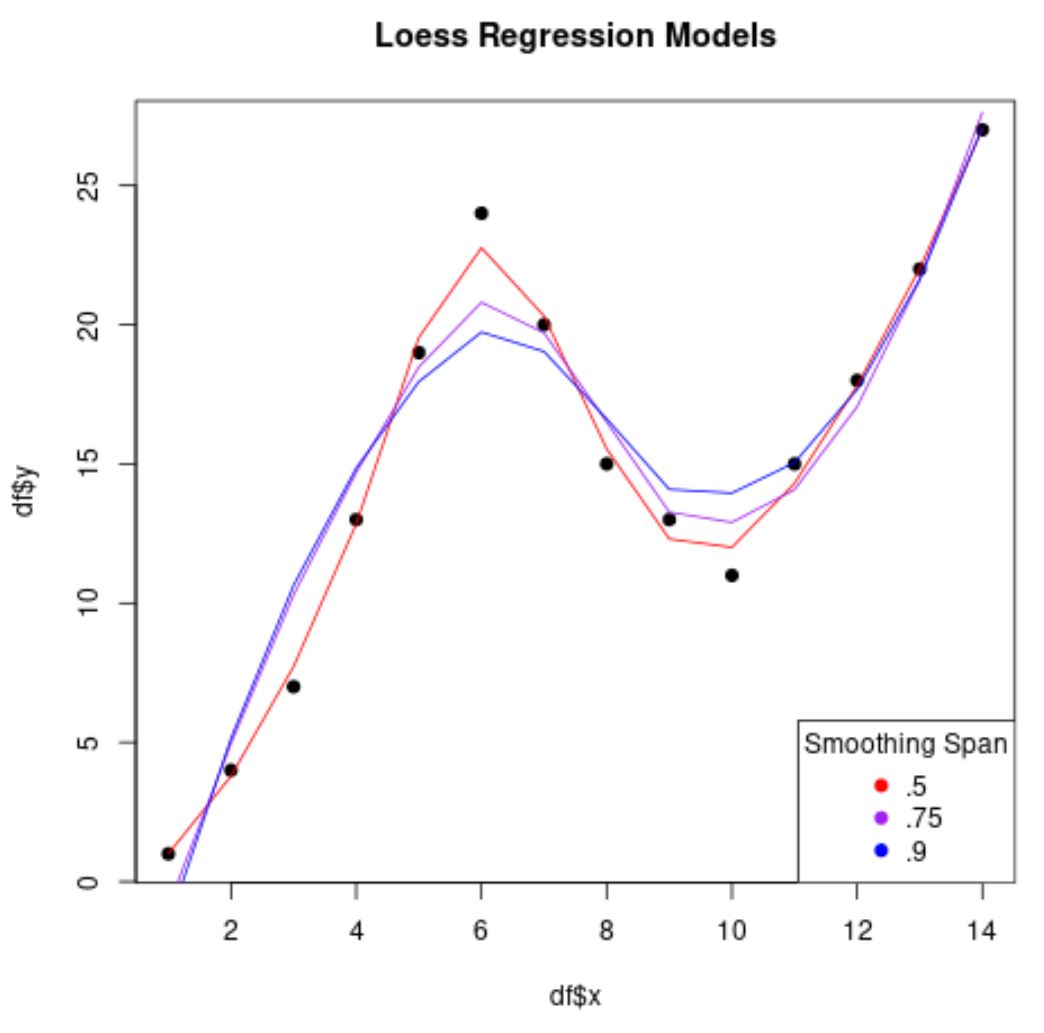
Notez que plus la valeur que nous utilisons pour span est faible, moins le modèle de régression sera « fluide » et plus le modèle tentera d’épouser les points de données.
Étape 3 : Utilisez la validation croisée K-Fold pour trouver le meilleur modèle
Pour trouver la valeur d’étendue optimale à utiliser, nous pouvons effectuer une validation croisée k-fold à l’aide des fonctions du package caret :
library(caret)
#define k-fold cross validation method
ctrl <- trainControl(method = "cv", number = 5)
grid <- expand.grid(span = seq(0.5, 0.9, len = 5), degree = 1)
#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = "gamLoess", tuneGrid=grid, trControl = ctrl)
#print results of k-fold cross-validation
print(model)
14 samples
1 predictor
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 12, 11, 11, 11, 11
Resampling results across tuning parameters:
span RMSE Rsquared MAE
0.5 10.148315 0.9570137 6.467066
0.6 7.854113 0.9350278 5.343473
0.7 6.113610 0.8150066 4.769545
0.8 17.814105 0.8202561 11.875943
0.9 26.705626 0.7384931 17.304833
Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.
Nous pouvons voir que la valeur de span qui a produit la valeur la plus faible pour l’ erreur quadratique moyenne (RMSE) est 0,7 .
Ainsi, pour notre modèle de régression LOESS final, nous choisirions d’utiliser une valeur de 0,7 pour l’argument span dans la fonction loess() .
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur les modèles de régression dans R :
Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression logistique dans R
Comment effectuer une régression quantile dans R
Comment effectuer une régression pondérée dans R
