Comment interpréter l’asymétrie dans les statistiques : avec des exemples
Dans le domaine des statistiques, nous utilisons l’asymétrie pour décrire la symétrie d’une distribution.
Nous disons qu’une distribution de valeurs de données est asymétrique si elle a une « queue » sur le côté gauche de la distribution :
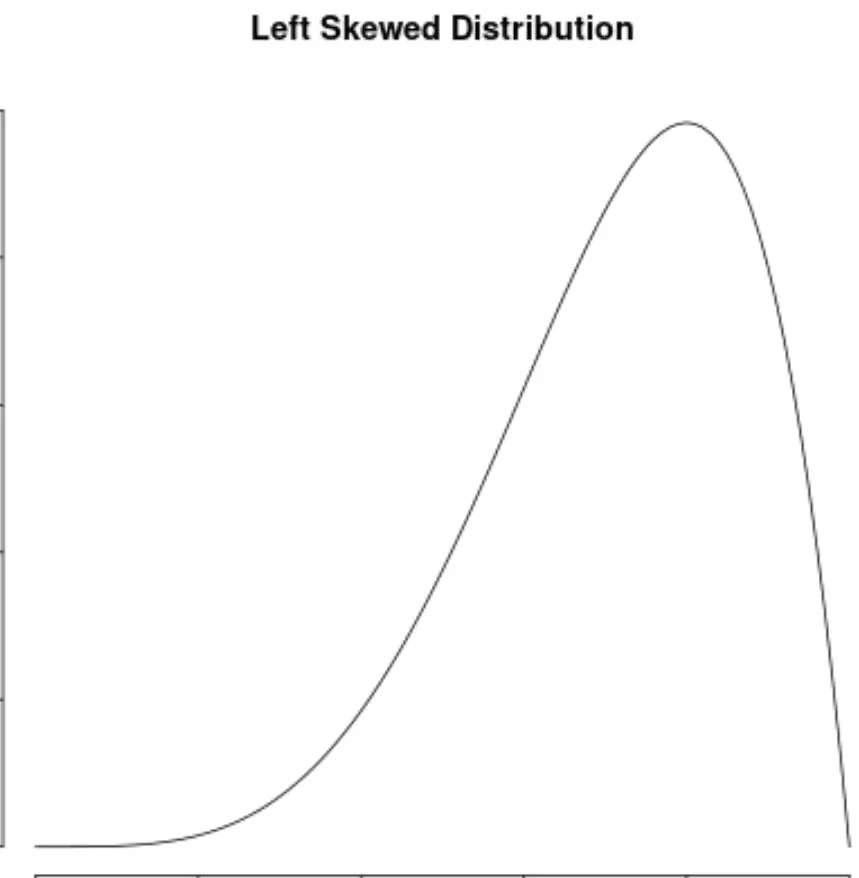
On dit qu’une distribution est asymétrique à droite si elle a une « queue » sur le côté droit de la distribution :
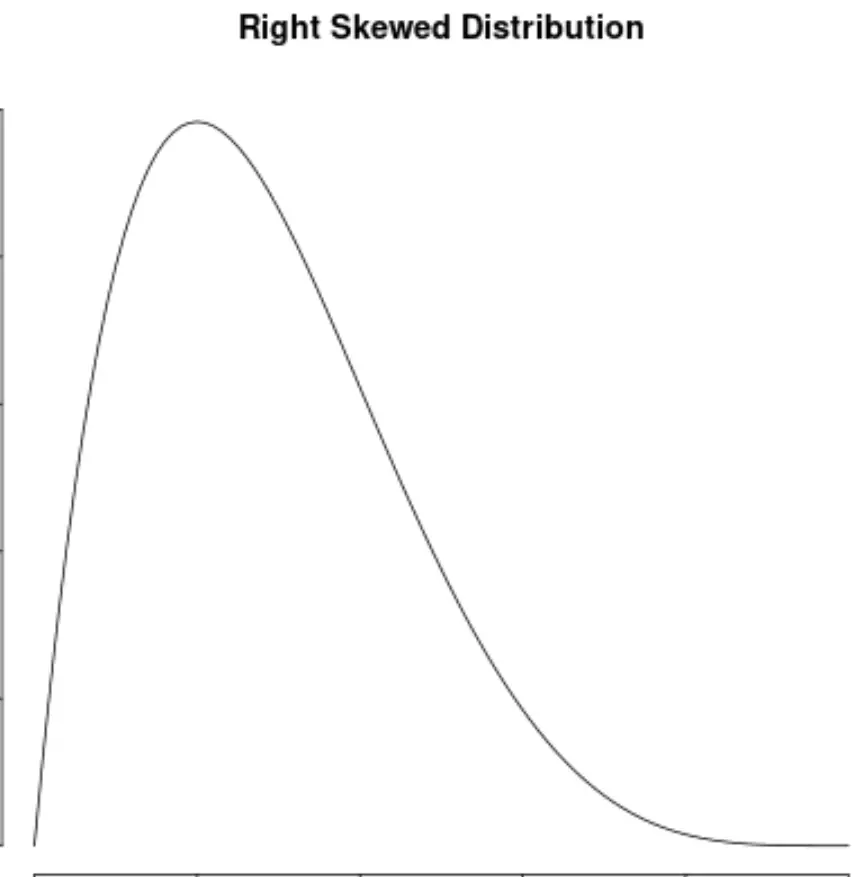
Et nous disons qu’une distribution n’a pas d’asymétrie si elle est symétrique des deux côtés :
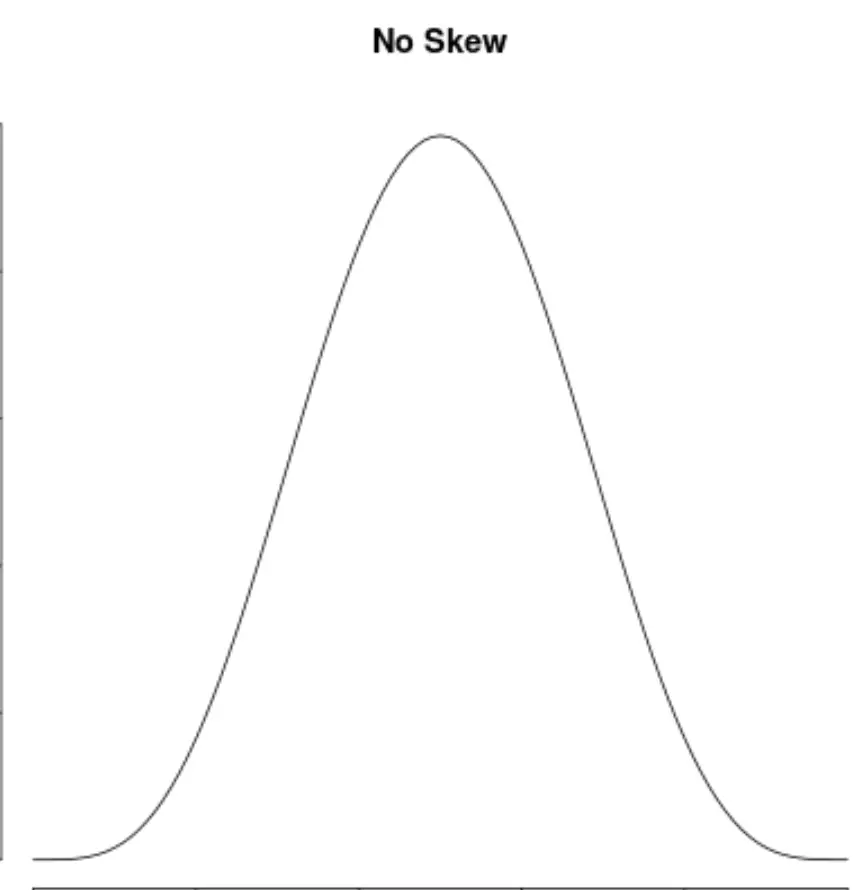
Comment interpréter l’asymétrie
La valeur de l’asymétrie peut aller de l’infini négatif à l’infini positif.
Voici comment interpréter les valeurs d’asymétrie :
- Une valeur négative pour l’asymétrie indique que la queue se trouve sur le côté gauche de la distribution, qui s’étend vers des valeurs plus négatives.
- Une valeur positive pour l’asymétrie indique que la queue se trouve du côté droit de la distribution, qui s’étend vers des valeurs plus positives.
- Une valeur de zéro indique qu’il n’y a aucune asymétrie dans la distribution, ce qui signifie que la distribution est parfaitement symétrique.
Les exemples suivants montrent comment interpréter les valeurs d’asymétrie dans la pratique.
Exemple 1 : distribution asymétrique à gauche
La répartition de l’âge des décès dans la plupart des populations est asymétrique à gauche. La plupart des gens vivent entre 70 et 80 ans, et de moins en moins vivent en dessous de cet âge.
Si nous créions un graphique de densité pour visualiser la distribution des valeurs pour l’âge du décès, cela pourrait ressembler à ceci :
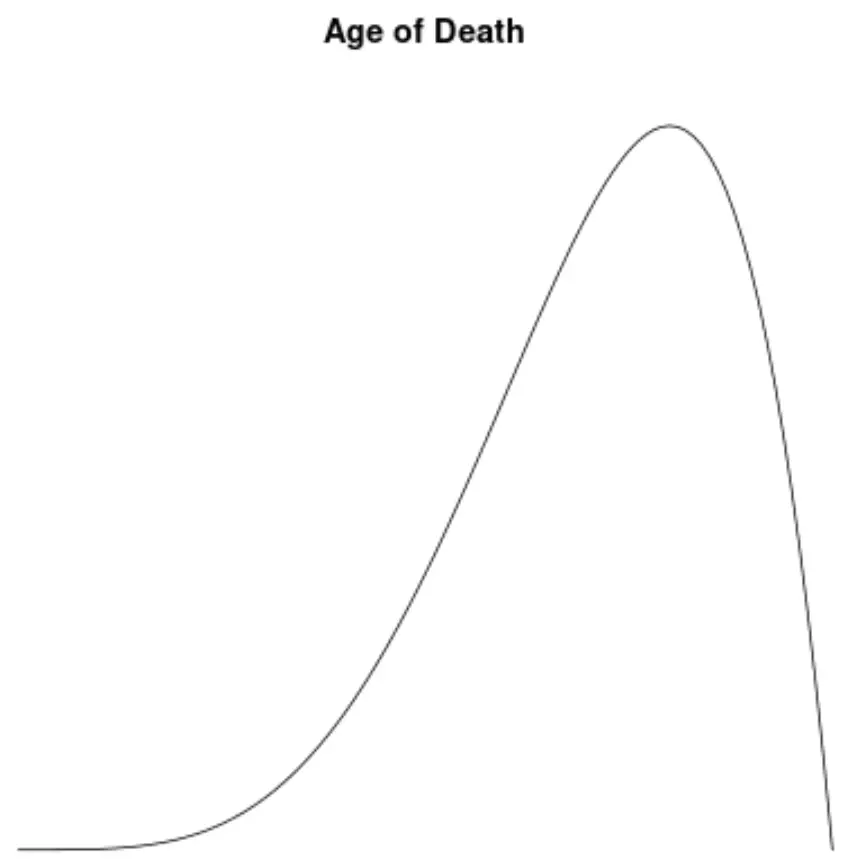
Supposons que nous calculions l’asymétrie de cette distribution et constatons qu’elle est de -1,3225 .
Puisque cette valeur est négative, nous interprétons cela comme signifiant que la distribution est asymétrique à gauche, ce qui signifie que la queue s’étend vers le côté gauche de la distribution.
Exemple 2 : distribution asymétrique à droite
La répartition des revenus des ménages aux États-Unis est asymétrique vers la droite, la plupart des ménages gagnant entre 30 000 et 70 000 $ par an, mais avec une longue queue droite de ménages gagnant beaucoup plus.
Si nous créons un graphique de densité pour visualiser la distribution des valeurs du revenu des ménages, cela pourrait ressembler à ceci :
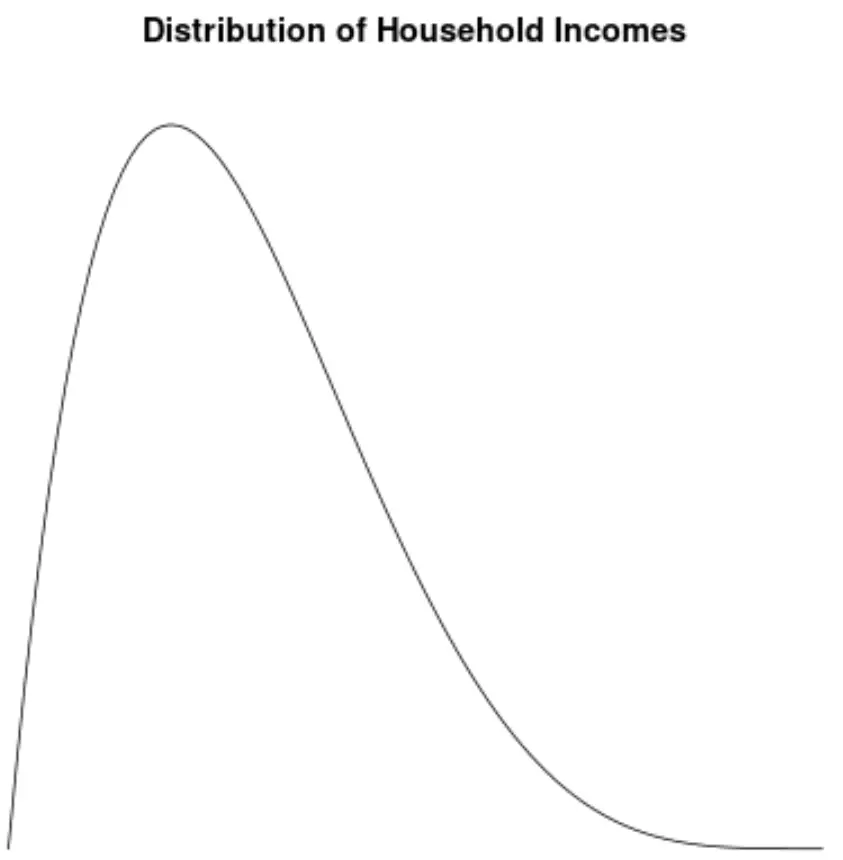
Supposons que nous calculions l’asymétrie de cette distribution et constatons qu’elle est de 2,0043 .
Puisque cette valeur est positive, nous interprétons cela comme signifiant que la distribution est asymétrique vers la droite, ce qui signifie que la queue s’étend vers le côté droit de la distribution.
Exemple 3 : Aucun biais
La taille des mâles est à peu près normalement répartie et ne présente aucune asymétrie. Par exemple, la taille moyenne d’un homme aux États-Unis est d’environ 69,1 pouces. La répartition des hauteurs est à peu près symétrique, certaines étant plus courtes et d’autres plus hautes.
Si nous créions un graphique de densité pour visualiser la répartition des tailles masculines aux États-Unis, cela pourrait ressembler à ceci :
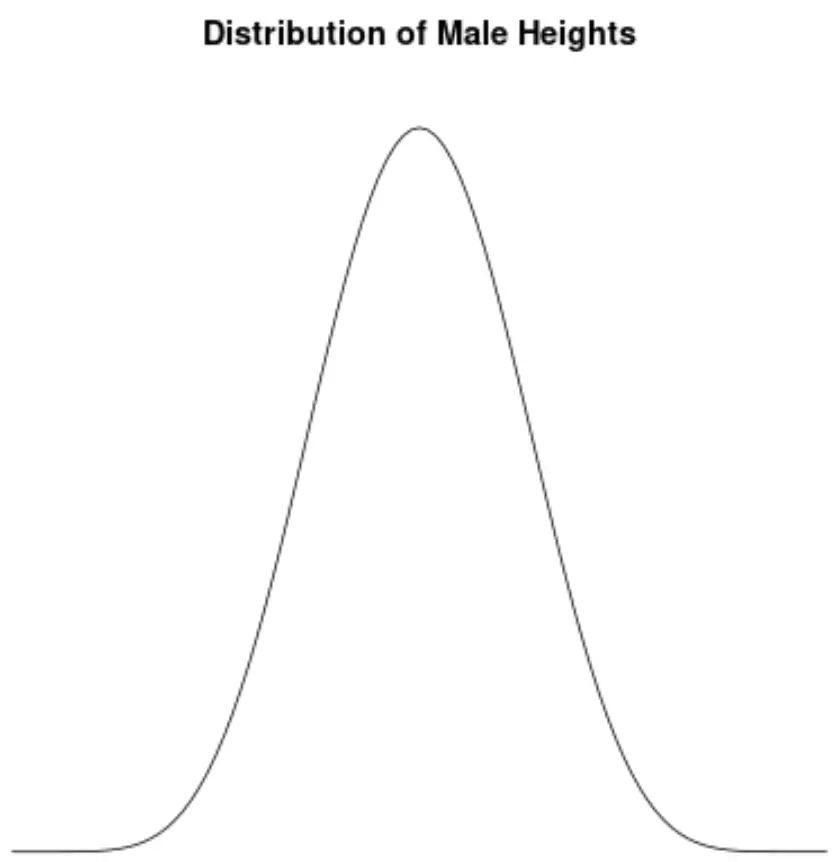
Supposons que nous calculions l’asymétrie de cette distribution et constatons qu’elle est de 0,0013 .
Puisque cette valeur est proche de zéro, nous interprétons cela comme signifiant que la distribution n’a pratiquement aucune asymétrie, ce qui signifie que les queues de chaque côté de la distribution sont à peu près égales.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur l’asymétrie des statistiques :
5 exemples de distributions positivement asymétriques
5 exemples de distributions négativement asymétriques
Comment calculer l’asymétrie dans Excel
Comment identifier l’asymétrie dans les diagrammes en boîte
