L’importance des statistiques dans l’éducation (avec exemples)
Le domaine des statistiques concerne la collecte, l’analyse, l’interprétation et la présentation des données.
Dans le contexte éducatif, les statistiques sont importantes pour les raisons suivantes :
Raison 1 : Les statistiques permettent aux éducateurs de comprendre les performances des élèves à l’aide de statistiques descriptives.
Raison 2 : Les statistiques permettent aux enseignants de repérer les tendances dans les performances des élèves à l’aide de visualisations de données.
Raison 3 : Les statistiques permettent aux éducateurs de comparer différentes méthodes d’enseignement à l’aide de tests d’hypothèse.
Dans la suite de cet article, nous développons chacune de ces raisons.
Raison 1 : Comprendre les performances des élèves à l’aide de statistiques descriptives
Les statistiques descriptives sont utilisées pour décrire les données.
Dans un contexte éducatif, un enseignant peut calculer les statistiques descriptives suivantes pour les élèves de sa classe :
- La note moyenne à un examen donné.
- L’écart type des scores à un certain examen.
- L’éventail des scores à un examen donné.
- Le pourcentage d’étudiants qui ont réussi un certain examen.
- Le 90e centile des résultats à un examen donné.
Grâce à ces mesures, l’enseignant peut mieux comprendre les résultats des élèves de sa classe à un examen donné.
Elle peut alors décider si elle doit modifier sa méthode d’enseignement si trop peu d’étudiants réussissent l’examen ou éventuellement proposer des possibilités de tutorat supplémentaires aux étudiants ayant de mauvais résultats à l’examen, etc.
Remarque : Ces types de statistiques descriptives sont utilisés à tous les niveaux d’enseignement. Par exemple, un directeur peut utiliser des statistiques descriptives pour surveiller les résultats aux examens des élèves de toute une école. Un ministère de l’Éducation d’un État peut également utiliser des statistiques descriptives pour surveiller les résultats des examens des étudiants de l’ensemble d’un État.
Raison 2 : repérer les tendances à l’aide de la visualisation des données
Une autre manière courante d’utiliser les statistiques dans l’éducation consiste à visualiser des données telles que des graphiques linéaires, des histogrammes, des boîtes à moustaches, des diagrammes circulaires et d’autres graphiques.
Ces types de graphiques sont souvent utilisés pour aider les éducateurs à repérer les tendances en matière de performances en classe et de performances individuelles des élèves.
Par exemple, supposons qu’un enseignant crée le graphique à barres suivant pour visualiser la note moyenne aux examens tout au long de l’année :
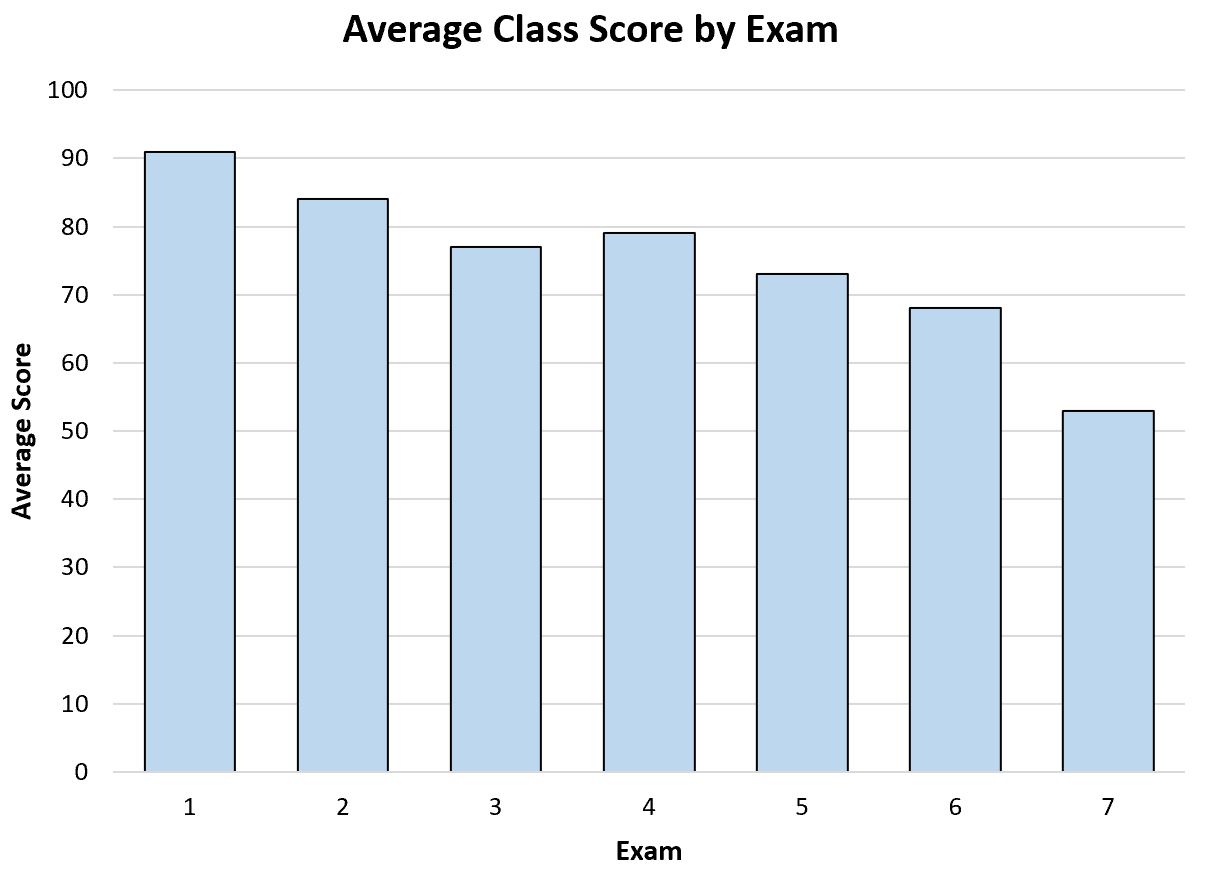
Rien qu’en regardant ce graphique à barres, l’enseignant pourra constater que la note moyenne aux examens des élèves de sa classe diminue lentement au fil de l’année.
Cela peut permettre à l’enseignant d’améliorer ses méthodes d’enseignement ou peut-être de faire passer une enquête à ses élèves pour leur demander leur avis sur ses méthodes d’enseignement, etc.
Raison 3 : Comparez les méthodes d’enseignement à l’aide de tests d’hypothèses
Les statistiques sont également utilisées dans l’éducation sous la forme de tests d’hypothèses .
Ce sont des tests que les éducateurs peuvent utiliser pour déterminer s’il existe une signification statistique entre différentes méthodes d’enseignement.
Par exemple, supposons qu’un enseignant souhaite déterminer si un certain programme d’études affecte les résultats des tests. Pour tester cela, il sélectionne au hasard 15 étudiants pour passer un pré-test. Ensuite, il fait utiliser à chaque élève le programme d’études pendant un mois puis un post-test de difficulté similaire.
Les résultats des tests de chacun des 15 étudiants sont indiqués ci-dessous :
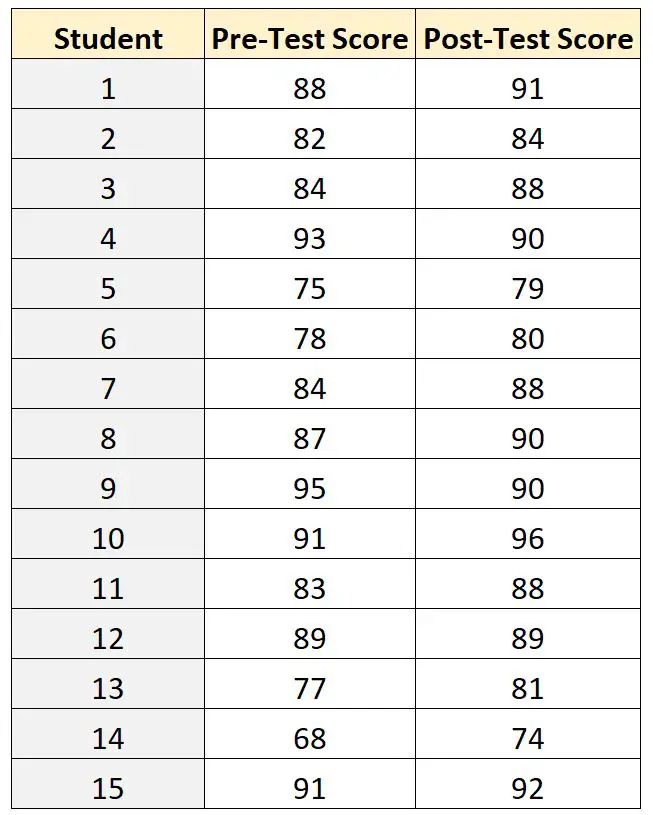
Pour comparer la différence entre les scores moyens au pré-test et au post-test, l’enseignant peut utiliser un test t pour échantillons appariés car pour chaque élève, son score pré-test peut être associé à son score post-test.
Supposons que le professeur utilise un logiciel statistique pour effectuer ce test t pour échantillons appariés et reçoive les résultats suivants :
- statistique du test t : -2,97
- Valeur p : 0,0101
Dans cet exemple, le test t pour échantillons appariés utilise les hypothèses nulles et alternatives suivantes :
- H 0 : Les scores moyens pré-test et post-test sont égaux
- H A : Les scores moyens pré-test et post-test ne sont pas égaux
Puisque la valeur p ( 0,0101 ) est inférieure à 0,05, nous rejetons l’hypothèse nulle.
Cela signifie que nous disposons de suffisamment de preuves pour affirmer que le score moyen au test est différent pour les étudiants avant et après leur participation au programme d’études.
Remarque : Ceci n’est qu’un exemple de test d’hypothèse utilisé en éducation. D’autres tests courants incluent un test t à un échantillon , un test t à deux échantillons , une ANOVA unidirectionnelle et une ANOVA bidirectionnelle .
Ressources additionnelles
Les articles suivants expliquent l’importance des statistiques dans d’autres domaines :
L’importance des statistiques dans les entreprises
L’importance des statistiques en économie
L’importance des statistiques dans les soins de santé
