Quand utiliser la corrélation de rang de Spearman (2 scénarios)

La manière la plus courante de quantifier l’association linéaire entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui prend toujours une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative
• 0 indique aucune corrélation linéaire
• 1 indique une corrélation linéaire parfaitement positive

Cependant, ce type de coefficient de corrélation fonctionne mieux lorsque la véritable relation sous-jacente entre les deux variables est linéaire .

Il existe un autre type de coefficient de corrélation appelé corrélation de rang de Spearman qu’il est préférable d’utiliser dans deux scénarios spécifiques :

Scénario 1 : Lorsque vous travaillez avec des données classées.

• Un exemple pourrait être un ensemble de données contenant le classement de la note d’un élève à l’examen de mathématiques ainsi que le classement de sa note à l’examen de sciences dans une classe.

Scénario 2 : Lorsqu’une ou plusieurs valeurs aberrantes extrêmes sont présentes.

• Lorsque des valeurs aberrantes extrêmes sont présentes dans un ensemble de données, le coefficient de corrélation de Pearson est fortement affecté.

Les exemples suivants montrent comment calculer la corrélation de rang Spearman dans chacun de ces scénarios.

Scénario 1 : Corrélation du classement de Spearman avec les données classées

Considérez l’ensemble de données suivant (et le nuage de points correspondant) qui montre la relation entre deux variables :

À l’aide d’un logiciel statistique, nous pouvons calculer les coefficients de corrélation suivants pour ces deux variables :

• Corrélation de Pearson : 0,79
• Corrélation des rangs de Spearman : 1

Dans ce scénario, si nous nous soucions uniquement du rang des valeurs des données (lorsque le rang de x augmente, le rang de y augmente-t-il également ?), alors la corrélation de rang de Spearman nous donnerait une meilleure idée de la corrélation entre les deux variables. .

Dans cet ensemble de données particulier, à mesure que le rang de x augmente, le rang de y augmente toujours .

La corrélation de rang de Spearman capture parfaitement ce comportement en nous indiquant qu’il existe une relation positive parfaite ( ρ = 1 ) entre les rangs de x et les rangs de y.

En revanche, la corrélation de Pearson nous indique qu’il existe une forte relation linéaire ( r = 0,79 ) entre les deux variables.

C’est vrai, mais ce n’est pas utile si l’on se soucie uniquement de la relation entre les rangs de x et les rangs de y.

Scénario 2 : Corrélation du classement de Spearman avec les valeurs aberrantes extrêmes

Considérez l’ensemble de données suivant (et le nuage de points correspondant) qui montre la relation entre deux variables :

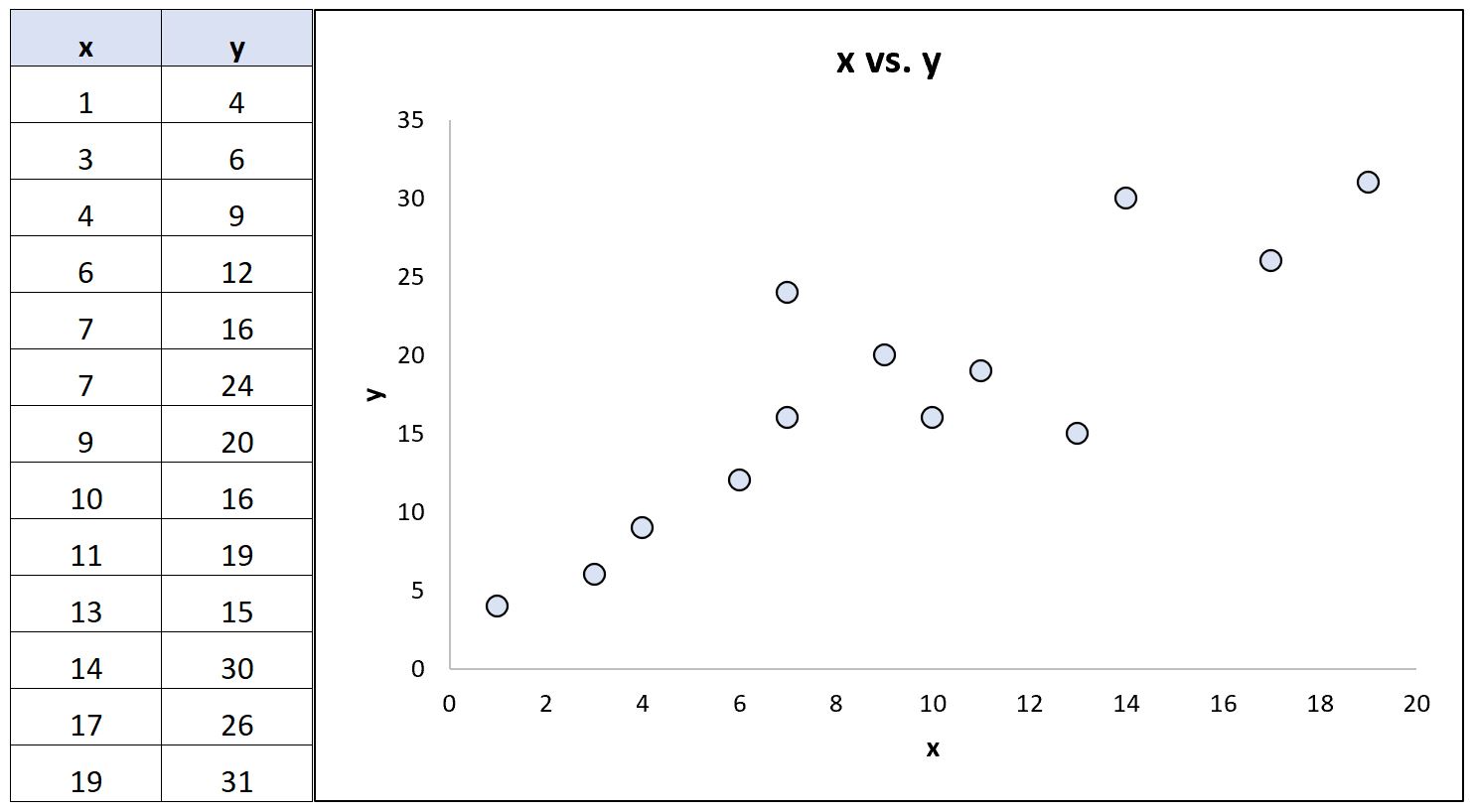
À l’aide d’un logiciel statistique, nous pouvons calculer les coefficients de corrélation suivants pour ces deux variables :

• Corrélation de Pearson : 0,86
• Corrélation des rangs de Spearman : 0,85

Les coefficients de corrélation sont presque identiques car la relation sous-jacente entre les variables est à peu près linéaire et il n’y a pas de valeurs aberrantes extrêmes.

Supposons maintenant que nous modifiions la dernière valeur y de l’ensemble de données pour qu’elle devienne une valeur aberrante extrême :

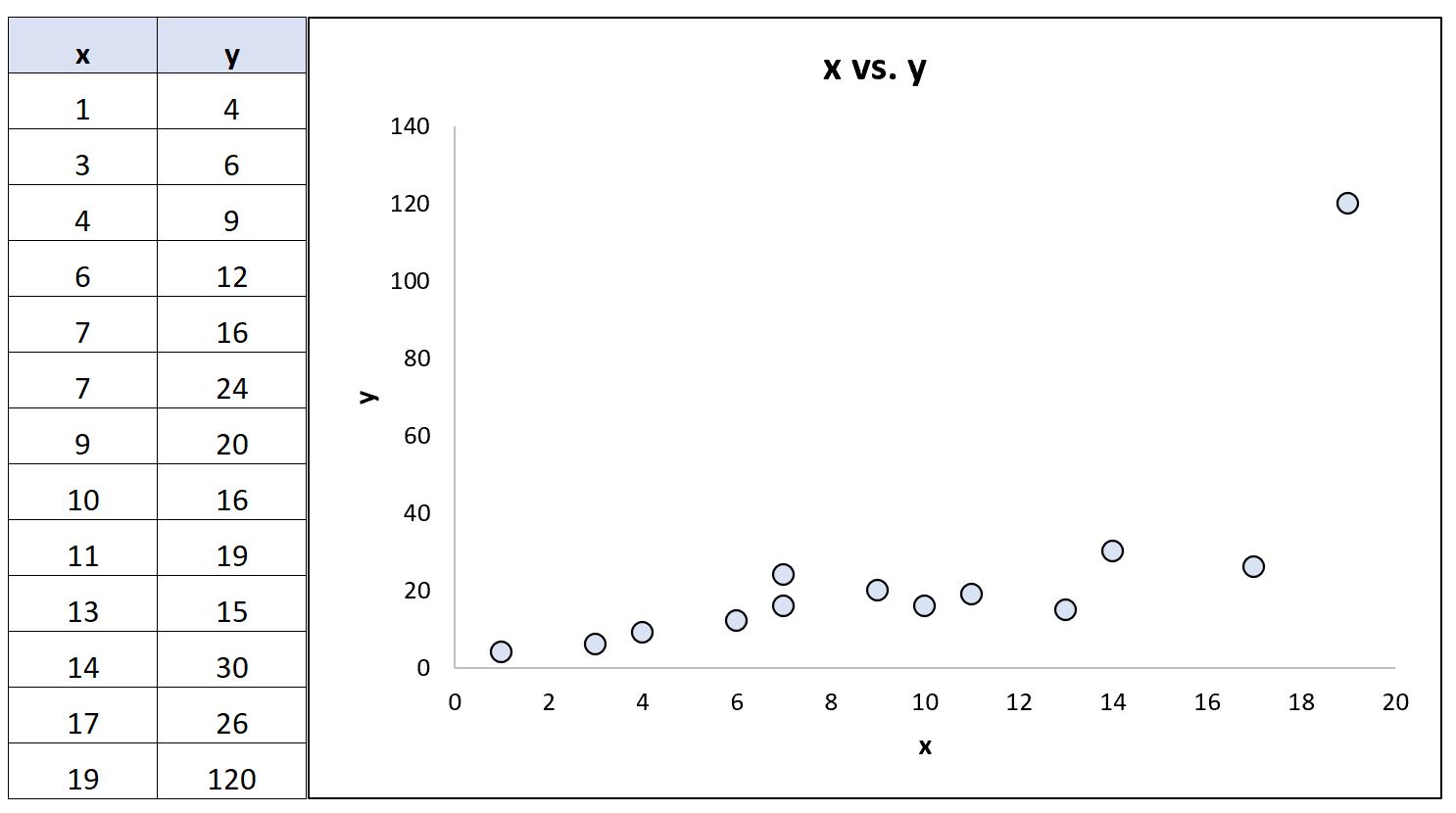
Grâce à un logiciel statistique, nous pouvons recalculer les coefficients de corrélation :

• Corrélation de Pearson : 0,69
• Corrélation des rangs de Spearman : 0,85

Le coefficient de corrélation de Pearson a changé considérablement tandis que le coefficient de corrélation de rang de Spearman est resté le même.

En utilisant le jargon statistique, nous dirions que la relation entre x et y est monotone (à mesure que x augmente, y augmente généralement) mais pas linéaire puisque la valeur aberrante influence énormément les données.

Dans ce scénario, la corrélation de rang de Spearman quantifie bien cette relation monotone, tandis que la corrélation de Pearson fait un mauvais travail car elle tente de calculer la relation linéaire entre les deux variables.

Connexes : Comment signaler la corrélation de rang de Spearman au format APA

Ressources additionnelles

Les didacticiels suivants expliquent comment calculer la corrélation de rang de Spearman à l’aide de différents logiciels :

Comment calculer la corrélation des classements Spearman dans Excel
Comment calculer la corrélation de classement de Spearman dans Google Sheets
Comment calculer la corrélation de rang de Spearman dans R
Comment calculer la corrélation de rang Spearman en Python