Pourquoi le mode est-il important dans les statistiques ?

Le mode représente la valeur qui apparaît le plus souvent dans un ensemble de données.

Un ensemble de données peut n’avoir aucun mode (si aucune valeur ne se répète), un mode ou plusieurs modes.

Par exemple, le mode dans l’ensemble de données suivant est 19 :

Ensemble de données : 3, 4, 11, 15, 19 , 19 , 19 , 22, 22, 23, 23, 26

C’est la valeur qui apparaît le plus souvent.

En statistiques, le mode est important pour les raisons suivantes :

Raison 1 : Cela nous permet de savoir quelle(s) valeur(s) dans un ensemble de données sont les plus courantes.

Raison 2 : c’est utile pour trouver la valeur la plus fréquente dans les données catégorielles lorsque la moyenne et la médiane ne peuvent pas être calculées.

Raison 3 : Cela nous donne une idée de l’endroit où se situe le « centre » d’un ensemble de données, même si la médiane et la moyenne sont plus couramment utilisées (comme nous le verrons plus loin dans cet article).

Les exemples suivants illustrent chacune de ces raisons dans la pratique.

Raison 1 : le mode nous indique quelle valeur est la plus courante

Supposons que nous ayons un ensemble de données de 100 000 lignes contenant le prix de vente des maisons aux États-Unis :

Supposons que nous utilisions un logiciel statistique (comme Excel , R , Python , etc.) pour calculer le mode de cet ensemble de données et constatons qu’il existe trois modes :

• 280 000 $
• 300 000 $
• 305 000 $

Cela nous donne immédiatement une idée des prix de l’immobilier les plus fréquents dans l’ensemble de données.

Le calcul du mode est également beaucoup plus rapide que de regarder des milliers de lignes de données et de tenter d’identifier les prix de l’immobilier qui se produisent le plus souvent.

Raison 2 : le mode recherche la valeur la plus courante dans les données catégorielles

Supposons que nous ayons un ensemble de données de 1 000 lignes qui nous indique la couleur de la voiture appartenant aux particuliers dans un certain quartier :

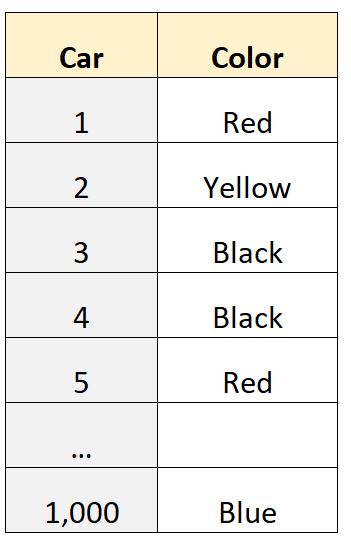
La variable « couleur » est une variable catégorielle , ce qui signifie que les valeurs appartiennent à des catégories (« rouge », « jaune », « noir », etc.) et nous ne pouvons donc pas calculer une valeur quantitative comme la moyenne ou la médiane.

Cependant, nous pouvons calculer le mode car il représente simplement la valeur la plus courante dans l’ensemble de données.

Par exemple, nous pourrions utiliser un logiciel statistique pour déterminer que le mode de cet ensemble de données est « noir », ce qui nous indique que la couleur de voiture la plus courante dans cet ensemble de données est le noir.

Raison 3 : le mode nous donne une idée de l’endroit où se trouve le centre d’un ensemble de données

Le mode est également considéré comme une mesure de tendance centrale , ce qui signifie qu’il peut nous donner une idée de l’endroit où se trouve le « centre » de l’ensemble de données.

Par exemple, supposons que nous disposions de l’ensemble de données suivant qui montre les résultats aux examens de 20 étudiants différents dans une classe :

Le mode s’avère être 82 – c’est la note d’examen la plus courante. Cela s’avère également être une bonne indication de l’endroit où se situe la valeur du score d’examen « central » dans cet ensemble de données.

Cependant, supposons que nous disposions à la place de l’ensemble de données suivant sur les résultats des examens :

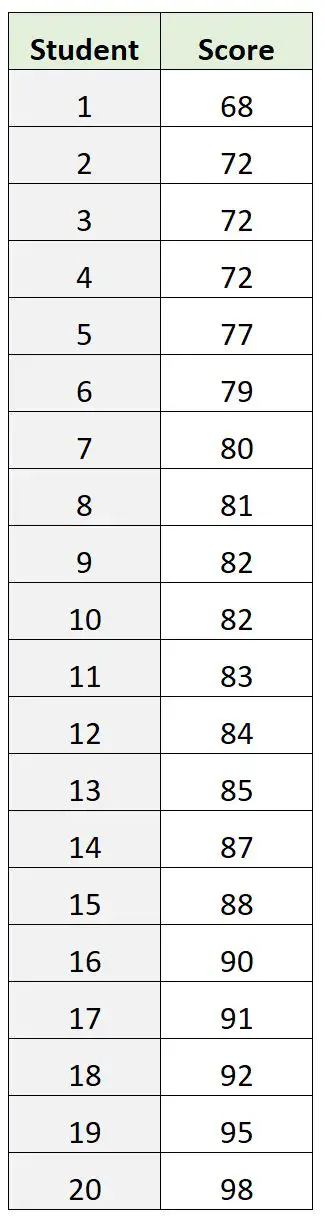
Dans cet ensemble de données, 72 est le score de l’examen de mode. Cependant, cela s’avère être une mauvaise indication de l’endroit où se situe la note « centrale » de l’examen.

Le score moyen à l’examen est de 82,9 et le score médian à l’examen est de 82,5 , ce qui nous donne tous deux une meilleure idée de l’endroit où se situe la valeur « centrale » par rapport au mode.

Résumé

Voici un bref résumé des principaux points abordés dans cet article :

• Le mode représente la ou les valeurs qui apparaissent le plus souvent dans un ensemble de données.
• Le mode nous indique la valeur la plus courante dans les données catégorielles lorsque la moyenne et la médiane ne peuvent pas être utilisées.
• Le mode nous donne une idée de l’endroit où se trouve le « centre » d’un ensemble de données, mais il peut être trompeur par rapport à la moyenne ou à la médiane.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la moyenne, la médiane et le mode dans les statistiques :

Pourquoi la moyenne est-elle importante en statistiques ?
Pourquoi la médiane est-elle importante dans les statistiques ?
Exemples concrets : utilisation de la moyenne, de la médiane et du mode
Quand utiliser la moyenne par rapport à la médiane : avec des exemples